12 растений с идеальной симметрией. Симметрия растений
Природная симметрия в мире растений
Природная симметрия, встречающаяся в живой природе, привлекала и интересовала человека с древних времен. Еще в Древней Греции, V веке до н. э., пифагорейцы обратили внимание на необыкновенную гармонию и биосимметрию живых растений. Многие века ученые изучали и исследовали структурные формы биообъектов, было написано масса интересных работ и сделано много открытий в этой области, что даже с 1961 года привело к выделению особого направления в учении о биосимметрики. Особенно красивой и завораживающей является осевая симметрия, наблюдаемая у растений, этот результат осевой симметрии достигается при повороте абсолютно одинаковых элементов, размещенных вокруг одного центра. Причем эти элементы, листочки, веточки или цветочки, могут располагаться…
Рейтинг пользователей 4.8 ( 1 голосов)Природная симметрия, встречающаяся в живой природе, привлекала и интересовала человека с древних времен. Еще в Древней Греции, V веке до н. э., пифагорейцы обратили внимание на необыкновенную гармонию и биосимметрию живых растений. Многие века ученые изучали и исследовали структурные формы биообъектов, было написано масса интересных работ и сделано много открытий в этой области, что даже с 1961 года привело к выделению особого направления в учении о биосимметрики.
Особенно красивой и завораживающей является осевая симметрия, наблюдаемая у растений, этот результат осевой симметрии достигается при повороте абсолютно одинаковых элементов, размещенных вокруг одного центра. Причем эти элементы, листочки, веточки или цветочки, могут располагаться под любым углом и с разной частотой, главное, чтобы вращение было вокруг одного центра. Например, этот эффект хорошо виден на фото картинках растений, приведенных ниже. Ведь симметрия это один из главных принципов красоты. Именно симметричные элементы больше воспринимаются человеком как единый и целостный объект. Симметричные формы больше и лучше запоминаются, и выглядят более понятными и простыми нежели ассиметричные элементы. Даже дизайнеры в своих работах гораздо чаще используют симметрию, для достижения баланса и гармонии, и получают приятный для глаза образ или целый объект.
allfreefoto.ru
Симметрия в мире растений
Введение
Наш симметричный мир...
Симметрия во всем:
В закате Солнца и в его восходе,
В живой и неживой природе,
В кристаллах, в музыке, в поэзии - во всем.
Симметрия - синоним совершенства,
Гармонии, высокой красоты.
Букашки, звери, человек, цветы -
Во всем симметрия, все совершенно.
Законы физики,
Вселенная сама,
Вся наша жизнь симметрии полна.
А без нее все было б косо, криво, неэстетично, просто некрасиво. [7]
Симметрия окружает нас повсюду. Понятие симметрии проходит через всю многовековую историю человеческого творчества. [4,4]
Меня очень заинтересовал этот вопрос, поэтому я решил провести исследование в этой области. Тема моего исследования «Симметрия в мире растений».
Цель исследования: существует ли симметрия в царстве растений и чем она обусловлена.
Задачи:
дать представление о симметрии в природе;
через понятие «симметрия» раскрыть важнейшие связи явлений симметрии с живой природой;
доказать, что действительно нас окружают симметричные предметы;
показать значимую роль симметрии в мире растений.
Гипотеза
Действительно ли встречается симметрия в мире растений и какую роль она играет?
Для решения поставленных задач я провёл собственное исследование, изучив материал из интернета, специальной литературы, анализируя внешний вид растений.
Основная часть
Глава 1. Что такое симметрия? Симметрия в мире растений.
«Симметрия» - слово греческого происхождения. Оно означает соразмерность, наличие определенного порядка, закономерности в расположении частей.
В толковом словаре Ожегова С. И и Шведовой Н. Ю. слово симметрия имеет следующее значение: соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости. [3,717]
Природа – удивительный творец и мастер. Все живое в природе обладает свойством симметрии.
Уместно привести слова известного немецкого математика Германа Вейля (1885 — 1955) о том, что посредством симметрии человек всегда пытался «постичь и создать порядок, красоту и совершенство».[4,7]
С симметрией в природе мы встречаемся не менее часто, чем в человеческом творчестве. Именно природа издавна учила человека понимать симметрию, а затем и пользоваться ею. Кто не любовался симметричными формами снежинок, кристаллов, листьев, цветов? Симметричны животные, рыбы, птицы, насекомые. Симметрично человеческое тело. [4,7]
Симметрия встречается уже у истоков человеческого знания, его широко используют все без исключения направления современной науки. Симметрия веками оставалась тем свойством, которое занимало умы философов, астрономов, математиков, художников, архитекторов и физиков. Древние греки были просто одержимы ею, и даже сегодня мы, как правило, стараемся применять симметрию во всем: от того, как мы располагаем мебель, до того, как мы укладываем наши волосы. Как только вы об этом задумаетесь, вы уже постоянно будете невольно искать симметрию в окружающих вас предметах. Что же такое симметрия? Какой глубокий смысл заложен в этом понятии? Почему симметрия буквально пронизывает весь окружающий нас мир? [4,4]
Мы отправимся в необычное путешествие, а именно, в путешествие в мир растений.
Растения окружают нас всюду: дома, в школе, на улице, в парке и лесу. Без этого царства растений Земля представляла бы голую безжизненную пустыню.
Древние греки и другие древние народы наделяли растение человеческими чертами. И это не случайно. Ведь растение, как и другой живой организм, дышит, питается, растет, размножается. [1,51]
В Древней Греции пифагорейцы обратили внимание на выявление симметрии в живой природе, в связи с развитием ими учения о гармонии. В 1961 году, как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика.
Глава 2. Виды симметрии.
Осевая (зеркальная) симметрия.
Центральная симметрия.
Поворотная симметрия.
Зеркально-поворотная симметрия.
Рассмотрим некоторые виды симметрии.
Осевая (зеркальная) симметрия.
Что может быть больше похоже на мою руку или моё ухо, чем их собственные отражения в зеркале? И всё же руку, которую я вижу в зеркале, нельзя поставить на место настоящей руки... Иммануил Кант [4,10]
Осевую симметрию часто называют зеркальной. Откуда такое название?
Внимательно приглядимся к окружающей нас природе. Рассмотрим обыкновенный листок. Форма его не является случайной, она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок. Одна из этих половинок положена зеркально относительно другой. Плоскость, разделяющая листок на две зеркально равные части называется «плоскостью симметрии». [прил. 3,а]
Ярко выраженной осевой симметрией обладают листья, ветви, цветы, плоды. Зеркальная симметрия характерна для листьев, но встречается и у цветов. [прил. 3,б]
Цветок анютины глазки имеет нечётное количество лепестков, поэтому он обладает осевой симметрией. [прил. 3,в]
Ярко выраженной симметрией обладают листья, ветви, цветы, плоды. [4,37]
Ситуация, когда присутствует только зеркальная симметрия, характерна для листьев, но встречается и у цветов. [4,37]
Центральную симметрию можно встретить повсюду. [прил. 3,г]
Центральную симметрию наблюдаем на изображении цветков одуванчика, мать-и-мачехи, сердцевины ромашки. [прил. 3,д]
Центральная симметрия характерна для цветов и плодов растений.
Остановимся на ягодах: голубика, черника, вишня и клюква. Рассмотрим разрез любой из этих ягод. Он представляет собой окружность, а окружность, как нам известно, имеет центр симметрии. [прил. 3,е]
Ромашка обладает центральной симметрией, т.к. её сердцевина представляет собой окружность. Весь цветок обладает центральной симметрией только в случае чётного количества лепестков. [прил. 3,ж]
Поворотная симметрия в природе.
Цветы издавна считаются символом красоты и совершенства. По словам известного математика Германа Вейля (1885-1955), человек на протяжении веков пытался постичь и то и другое посредством симметрии. [прил. 3,з]
Как истинный учёный, он считал, что цветы достойны внимания исследователя, потому что обладают свойством поворотной симметрии, весьма распространённой в мире растений. Биологи с математиками согласны: характер симметрии в строении цветка служит одним из его существенных признаков.
Слово «симметрия» знакомо нам с детства. Глядя в зеркало, мы видим симметричные половинки лица, глядя на ладошки, мы тоже видим зеркально-симметричные объекты. Взяв в руку цветок ромашки, мы убеждаемся, что путём поворотов её вокруг стебелька, можно добиться совмещения разных частей цветка. Это уже другой тип симметрии: поворотный. [6]
В многообразном мире цветов встречаются поворотные оси симметрии разных порядков. Однако наиболее распространена поворотная симметрия 5-го порядка. Эта симметрия встречается у многих полевых цветов (колокольчик, незабудка, луговая герань, лесная звездчатка, гвоздика, зверобой, лапчатка гусиная и др.), у цветов плодовых деревьев (вишня, яблоня, груша, мандарин и др.), у цветов плодово-ягодных растений (земляника, ежевика, малина, калина, черёмуха, рябина, боярышник, шиповник и др.), у ряда садовых цветов (настурция, флокс и др.). [4,38]
Симметрия и асимметрия настолько взаимосвязаны, что должны рассматриваться как две стороны единого понятия. Наш мир — это не просто симметричный мир. Это симметрично-асимметричный мир. Довольно точно выразился известный французский поэт Поль Валери (1871 – 1945): «Мир беспорядочно усеян упорядоченными формами» [4,137]
Поговорим подробнее о поворотной симметрии.
Всякий раз при повороте на угол каждый лепесток встаёт на место соседнего и после n таких перемещений в одном направлении занимает исходное положение. Таким образом, порядок поворотной симметрии цветка определяется, по сути, числом лепестков.
Например, цветок молочая имеет ось поворотной симметрии 2 порядка. [прил. 3,и]
Ирис – поворотная симметрия 3 порядка. [прил. 3,к]
Нередко встречаются цветы с поворотной симметрий 4-го порядка (сирень, чистотел). [прил. 3,к]
Растения 6-го порядка (лилия, шафран) [прил. 3,л]
Растения 8-го порядка (космея, сангвинария) [прил. 3,м]
Растения 5-го (герань, лютик) [прил. 3,н]
Зеркально-поворотная симметрия
Идея симметрии часто служила учёным путеводной нитью при рассмотрении проблем мироздания. [4,33]
В своей книге «Этот правый, левый мир» М. Гарднер пишет: «На Земле жизнь зародилась в сферически симметричных формах, а потом стала развиваться по двум главным линиям: образовался мир растений, обладающих симметрией конуса…[4,36]
Характерная для растений симметрия конуса хорошо видна на примере фактически любого дерева [4,36] [прил. 3,о] Это проявление вертикальной поворотной оси и вертикальной плоскости симметрии, что определено силой тяжести.
Если фигуру повернуть вокруг некоторой точки на 360°, то фигура совместится сама с собой. Точно так же можно повернуть фигуру 4 раза на 90 градусов и т. д. Каждый раз мы получим симметричные фигуры.
Для цветов характерна поворотная симметрия. [4,37] Цветок зверобоя имеет поворотную ось 5-го порядка и не обладает зеркальной симметрией. [4,37] [прил. 3,п]
Часто поворотная симметрия цветов сочетается с зеркальной симметрией. [4,37]
Веточка акации имеет зеркальную и переносную симметрию. [4,37] [прил. 3,р]
Веточка боярышника обладает скользящей осью симметрии. [4,38] [прил. 3,р]
Двусторонней симметрией обладают листья многих растений. [прил. 3,с]
Цветки, имея двойные части, считаются цветками с двойной симметрией.
Лучевая симметрия
Присмотритесь внимательно и вы увидите, что лепестки каждого тела расходятся во все стороны, как лучи от источника света. В математике - это симметрия относительно точки, в биологии – лучевая симметрия. [прил. 3,т]
Наследственность – это тоже симметрия.
Человек передает свои наследственные признаки из поколения в поколение. Так же растения переходя от одного поколения к другому, наблюдается сохранение определенных свойств. Так из семечка подсолнечника вырастает новый подсолнух (подсолнечник) с таким же огромным соцветием – корзинкой, также исправно поворачивается к Солнцу. Это тоже есть симметрия, ее называют наследственностью. [прил. 3,у]
Заключение.
Симметрия в природе противостоит хаосу, беспорядку. Она присутствует в нашей жизни буквально во всём. Некоторым она кажется скучной, некоторые любят её за спокойствие. Но как бы мы не относились к симметрии, она есть в нашей жизни, добавляя в неё мир, красоту. гармонию.
Проведя исследование различных источников информации о симметрии, я пришёл к выводу, что природа устроена в соответствии с законами симметрии. Все живое в природе обладает свойством симметрии.
Выводы:
Симметрия проникла в растительный мир, стала там полновластной хозяйкой.
2. В растительном мире встречается билатеральная (зеркальная), лучевая, поворотная, симметрия конуса., осевая, центральная, наследственная симметрия, винтовая симметрия.
3. В любом растении можно найти какую-то его часть обладающую осевой, центральной или винтовой симметрией.
4. Центральная симметрия наиболее характерна для плодов растений и некоторых цветов.
5. Симметрия форм, окраски цветов придаёт им красоту.
Считаю, что моя работа отражает явление симметрии в мире растений. Она имеет познавательную и практическую ценность. Материалы данной работы можно применять в повседневной жизни, при изучении тем на других предметах.
Симметрия окружает человека, находя своё проявление как в живой, так и в неживой природе. Объяснение законов симметрии важно для понимания красоты, гармонии, жизни. Результаты проекта будут интересны для учащихся средней и младшей школы.
Растения хорошо приспособились к жизни в разных условиях. [1,56] Мы должны помнить, что бережное отношение помогает сохранить природу не только для себя, но и для будущих поколений, чтобы и наши дети могли наслаждаться покоем и отдыхом в чудесном зеленом царстве растений. [1,81]
Чтобы познать тайны природы, тайны растительного мира, нужно все замечать вокруг, разглядывать понравившийся кустик, травинку, цветок и выражать свое восхищение природой…рассматривать их… восторгаться их красотой, неповторимостью. [2,15]
Человек, понимающий жизнь природы и глубоко ее любящий, всегда будет ее верным защитником, не принесет ей вреда. [2,28]
Зоркий глаз, пытливый ум
Для природы уникум!Красоту оберегай,
И в обиду не давай!
Все в природе подмечай,
Если нужно выручай!
Список использованных источников и литературы.
Зверев А. Т. Экология: учебник для 2 класса общеобразовательных школ. – М.: Дом педагогики, 1998. – 112 с., ил.
Минаева В. М. Экологическое воспитание в начальных классах: Пособие для учителя. – Мн.: Нар. Асвета, 1987. - - 112 с.
Ожегов С. И., Шведова Н. Ю. толковый словарь русского языка: 80000 слов и фразеологических выражений/Российская академия наук. Институт русского языка им. В. в. Виноградова. – 4-е изд., дополненное. – М.: Азбуковник, 1998. – 944 стр.
Тарасов Л. В.Т19. Этот удивительно симметричный мир: Пособие для учащихся. — М.: Просвещение, 1982. — 176 с, ил.
http://otherreferats.allbest.ru.
http://nsportal.ru/blog/shkola/matematika/all/2015/04/30/moi-stihi-o-simmetrii.
https://ru.wikipedia.org.
Приложение.
Загадки о цветах.
Много лепестков атласных –
Желтых, белых, пестрых, красных.
На меня ты погляди-ка,
Называюсь я …. гвоздика
Замечательный цветок,
Он как яркий огонек,
Пышный, важный, словно пан,
Распускается …..тюльпан
Посмотрите – у ограды
Расцвела царица сада.
Не тюльпан и не мимоза,
А в шипах красотка ….роза
Пышный, круглый, как кочан
Головой нам покачал.
Летом расцветает он,
Замечательный ….пион
Разукрашиваем летом
Клумбы, парки, цветники.
Мы своим морковным цветом,
А зовемся…..ноготки
Поворачиваем ловко
Он за солнышком головку.
Поле словно в желтых волнах.
Здесь цветет цветок ….подсолнух
Словарь
Асимметрия – отсутствие, нарушение симметрии.
Гармония – согласованность, стройность в сочетании чего-нибудь.
Герман Вейль – немецкий математик и физик-теоретик.
Закономерность – соответствие, отвечающее законам.
Иммануил Кант – немецкий философ, основатель «критицизма» и «немецкой классической философии»; профессор университета в Кенигсберге, иностранный почетный член Петербургской АН (1794).
Кристалл – твердое тело, имеющее упорядоченное, симметричное строение.
Лучевая симметрия – форма симметрии, при которой тело (или фигура) совпадает само с собой при вращении объекта вокруг определённой точки или прямой. Часто эта точка совпадает с центром симметрии объекта, то есть той точкой, в которой пересекается бесконечное количество осей или плоскостей двусторонней симметрии. Радиальной симметрией обладают такие геометрические объекты, как круг, шар, цилиндр или конус.
Наследственность – свойства организмов повторять от поколения к поколению сходные природные признаки.
Ожегов С. И. – советский лингвист, лексикограф, доктор филологических наук, профессор.
Симметрия – соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости.
Синоним – слово или выражение, совпадающее или близкое по значению с другим словом, выражением.
Совершенство – полнота всех достоинств, высшая степень какого-нибудь положительного качества.
Соразмерность – правильность в соотношении своих размеров, частей, в своем строении, пропорциональность.
Уникум – неповторимый, единственный в своем роде предмет, человек.
Хаос – отсутствие порядка, полная путаница.
Шведова Н. Ю. – советский и российский лингвист, доктор филологических наук, профессор, академик РАН.
Фотографии растений
а)
б)
зеркальная симметрия
в)
осевая симметрия
г)
центральная симметрия
д)
центральная симметрия
е)
центральная симметрия
ж)
Ромашка обладает центральной симметрией
з)
Герман Вейль (1885 - 1955)
и)
Цветок молочая – поворотная симметрия 2 - го порядка
к)
Ирис – поворотная симметрия 3 - го порядка
Сирень, чистотел – поворотная симметрия 4 – го порядка
л)
Лилия – 6 – го порядка
Шафран – 6 – го порядка
м)
Космея, сангвинария – 8 – го порядка
н)
Герань, лютик – 5 – го порядка
о)
Симметрия конуса
п)
Цветок зверобоя - поворотная ось 5 – го порядка
р)
Веточка акации – зеркальная и переносеая симметрия.
Веточка боярышника обладает скользящей осью симметрии.
с)
Двусторонняя симметрия
т)
Лучевая симметрия
у)
Подсолнечник. Наследственность в симметрии
infourok.ru
Симметрия в царстве растений - HintFox
«Симметрия является той идеей с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство»
Герман Вейль.
В летние каникулы я прочитала книгу для детей, написанную известным американским физиком Робертом Вудом. В шутливой форме автор дает читателям рецепты, «как отличить птиц от цветов», будто бы чрезвычайно сходных между собой. На приложенных карикатурных зарисовках наглядно демонстрируется сходство вороны и крокуса, перепела и капусты, клевера и ржанки и т. д.
Рассматривая эти занятные картинки, я задумалась и невольно задалась вопросом: а нет ли действительно чего-то общего в формах растений и животных? Возможно существуют какие-то причины, придающие такое неожиданное сходство самым разнообразным телам? Внимательно приглядимся к окружающей нас природе. Рассмотрим обыкновенный листок.
Форма его не является случайной, она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок. Одна из этих половинок положена зеркально относительно другой. Плоскость, разделяющая листок на две зеркально равные части называется «плоскостью симметрии».
Мы ее можем мысленно разделить вдоль на две зеркально равные части. Даже пятнистый узор на ее крыльях подчиняется такой геометрии. Все подчиняется такой «симметрии листка». Рассмотрим цветок ромашки.
Вокруг оранжевой серединки, как лучи вокруг солнышка, расположены лепестки. Ее тоже можно разделить на 2 зеркальные половинки по линии ее стебля, проходящей через его центр продолжающийся вдоль середины любого из лепестков или между ними. Этот цветок обладает многими плоскостями симметрии. Рассмотрим обыкновенный гриб.
Его можно разрезать вдоль ножки и через середину его шляпки он тоже обладает многими центрами симметрии. Следовательно, грибная симметрия родственна симметрии ромашки. Такая симметрия называется «ромашково-грибная симметрия».
Итак, два вида симметрии с необычным упорством повторяются вокруг нас. И я задалась целью: существует ли симметрия в царстве растений и чем она обусловлена. Для ее реализации много были сформулированы следующие задачи:
1. Познакомиться с геометрическими законами симметрии
2. Выявить причины, обуславливающие упорядоченность, пропорциональность растений.
1. Основные понятия о симметрии и геометрии растений.
1. 1. Развивающееся учение о симметрии.
Слово «симметрия» от греческого symmetria — соразмерность. Именно она позволит охватить самые разнообразные тела с единых геометрических позиций. С точки зрения биологии существует два типа симметрии: билатеральная и радиально – лучевая.
История науки показывает, что учение о симметрии развивалось крайне медленно и трудно. Поражающе правильные очертания кристаллов вызывали в древности суеверные представления. Красота и гармония природной симметрии наталкивали даже испытанных мудрецов на самые фантастические мысли.
Перейдем к знакомству с научными строго математическими понятиями, относящимися к симметрии. Прежде всего, обратимся к определению симметричной фигуры: «фигура называется симметрично, если она состоит из равных, закономерно повторяющихся частей». В этом определении требует пояснения два пункта: во-первых, следует выяснить, что подразумевается под словом «закономерность»,во-вторых, надо уточнить понятие о равенстве частей.
Говоря о равенстве частей, мы касаемся вопроса о равенстве фигур вообще. Приведем обобщающую формулировку данного понятия: «две фигуры называются взаимно равными, если для каждой точки одной фигуры обязательно найдется соответственная точка в другой фигуре, соответственная точка другой фигуре, причем расстояние между любыми двумя точками одной фигуры равно расстоянию между двумя соответственными точками другой. Действительно равными обычно называют такие фигуры которые при наложении одна на другую совпадают всеми своими точками. В качестве примера можно взять совершенно одинаковые правые (или две левые) перчатки. Такие равные фигуры называются «совершенно равными»
Перейдем к разбору второго пункта в приведенном выше определении симметричных фигур. Там упоминалась «закономерная повторяемость равных частей фигуры». В чем же она заключается? В сущности, для точной характеристики (вернее целого ряда закономерностей) нам придется воспользоваться вспомогательными геометрическими образами, относительно которых определенным правильным образом повторяются равные части симметричных фигур. Такие вспомогательные образы называются «элементами симметрии». Они точно помогают характеризовать симметрию фигур.
Начнем с плоскости симметрии. Плоскостью симметрии называется такая плоскость, которая делит фигуру на две равные части, расположенные друг против друга так, как предмет и его зеркальное отражение. Действие плоскости симметрии можно уподобить отражению в двустороннем зеркале, играющем роль этой плоскости.
Двустороннее отражение фигуры в плоскости симметрии называется «операцией симметрии». К операциям симметрии относятся повороты фигур вокруг определенных осей и отражения в особых точка, и т. д.
Ко всем таким операциям предъявляется одно основное требование после их проведения отраженная или повернутая фигура должна занять в пространстве тоже положение, которое она занимала до этих операций, хотя на месте одних ее точек придут другие соответственные точки. При этом фигура совмещается сама с собой.
2. Геометрическое определение симметрии
Симметрия – 1) инволютивное ортогональное преобразование, изменяющее ориентацию; инволютивность преобразования означает, что двукратное применение его дает тождественное преобразование. Например отражение относительно плоскости ( в пространстве (относительно прямой а на плоскости) есть симметрия при которой каждая точка М переходит в точку М’ , такую что отрезок ММ’ перпендикулярен плоскости ( (прямой а) и делится ею пополам. Плоскость ( (прямая а) называется плоскостью (осью) симметрии .
Любое ортогональное преобразование можно осуществить последовательным выполнением конечного числа отражений.
2) Симметрия – свойство геометрической фигуры Ф совмещается с собой при действии некоторой группы G ортогональных преобразований, называется группой симметрии Ф; таким образом симметрия отражает некоторую правильность формы фигуры, инвариантность ее при действии преобразований из G. Например, если на плоскости фигура Ф такова что повороты относительно какой-либо точки на угол 3600/n, n – целое, переводят ее в себя, то Ф обладает симметрией n-го порядка, а О называют центром симметрии n-го порядка .
здесь G – циклическая группа n-го порядка. Окружность обладает симметрией бесконечного порядка (поскольку совмещается с собой поворотом на любой угол).
Простейшими видами пространственной симметрии, помимо симметрии, порожденной отражениями, являются: а) симметрия относительно прямой n-го порядка; в этом случае фигура накладывается на себя вращением вокруг некоторой прямой (оси симметрии) на угол 3600/n. Например, плоская фигура симметричная относительно прямой АВ, имеет в пространстве эту прямую осью симметрии 2-го порядка .
Куб имеет прямую АВ осью симметрии 3-го порядка, а прямую CD – осью симметрии 4-го порядка ;
Вообще, правильные и полуправильные многогранники симметричны относительно ряда прямых. Расположение, количество и порядок осей симметрии играют основную роль в кристаллографии.
б) симметрия переноса; в этом случае фигура накладывается на себя переносом вдоль некоторой прямой (оси переноса) на какой-либо отрезок. Например, фигура с единственной осью переноса обладает бесконечным множеством плоскостей симметрии (поскольку любой перенос можно осуществить двумя последовательными отражениями), перпендикулярных оси переноса .
Фигуры, имеющие несколько осей переноса, играют важную роль при исследовании кристаллических решеток.
Комбинации симметрии, порожденные отражениями и вращениями (исчерпывающие простейшие виды симметрии конечных фигур), а также переносами, представляют интерес и являются предметом исследования в различных областях естествознания, искусство и т. д. Например, винтовая симметрия, осуществляемая поворотом на некоторый угол вокруг оси, дополненным переносом вдоль той же оси наблюдается в расположении листьев у растений .
Симметрия широко распространена как один из приемов построения бордюров и орнаментов (плоских фигур, обладающих одной или несколькими симметриями переноса в сочетании с отражениями) .
3. Центральная симметрия
Центральная симметрия как частный вид поворота вокруг заданной точки, обладает всеми свойствами поворота. В частности, при центральной симметрии сохраняются расстояния, поэтому центральная симметрия есть перемещение. Отсюда следует, что если одна из двух фигур отображается на другую центральной симметрией, то эти фигуры равны.
Выполним преобразование центральной симметрии около некоторого центра симметрии О .
Пусть А – произвольная точка плоскости, отличная от центра О симметрии. Проведем луч АО. На этом луче от точки О отложим отрезок ОВ, равный отрезку АО. (В(Ф). Точка В будет симметричной точке А относительно центра О.
Действительно угол АОВ развернутый; ( ОВ( = ( ОА( , поэтому, если плоскость повернуть вокруг центра О на 1800, то точка А отобразится на точку В, а точка В – на точку А.
Следовательно, если точка А симметрична точке В относительно центра О, то и, обратно, точка В симметрична точке А относительно центра О.
Приведенные рассуждения позволяют сформулировать следующее правило построения точки В, симметричной точке А (А(О) относительно центра О:
1) через точку А и центр симметрии О провести прямую;
2) на прямой точкой О задаются два луча. На луче, не содержащем точку А, построить точку В такую, что ( ОВ( = ( ОА(.
Поскольку центральная симметрия есть перемещение, она обладает всеми общими свойствами перемещений. В частности, точки принадлежащие одной прямой, отображаются на точке, также расположенные на одной прямой. Не трудно обнаружить что прямые симметричные относительно центра параллельны.
В самом деле, если бы две различные симметричные друг другу относительно центра прямые имели бы одну общую точку то они имели бы вторую общую точку, симметричную первой. Это противоречит аксиоме, что через две различные точки проходит только одна содержащая их прямая.
Прямая, проходящая через центр симметрии отображается центральной симметрией на себя.
Для каждой точки плоскости существует единственная ей симметричная точка относительная данного центра; если точка А совпадает с центром симметрии то и симметричная ей точка В совпадает с центром симметрии.
Подобно тому как осевая симметрия однозначно определяется своей осью, так и центральная симметрия однозначно определяется своим центром.
Некоторые фигуры имеют центр симметрии это значит, что для каждой точки этой фигуры центрально симметричная ей точка также принадлежит этой фигуре. Такие фигуры называют центрально-симметричными. Например, отрезок – центрально симметричная фигура, центром симметрии которой служит его середина; прямая – центрально-симметричная фигура относительно любой ее точки; окружность – центрально-симметричная фигура относительно ее центра; пара вертикальных углов есть центрально-симметричная фигура с центром симметрии в общей вершине углов.
4. Осевая симметрия фигур
Рассматривая различные фигуры, мы замечаем что некоторые из них симметричны относительно оси, т. е. отображаются себя симметрии относительно этой оси.
Ось симметрии делит такую фигуру на две симметричные фигуры расположенные в разных полуплоскостях определяемых осью симметрии.
Некоторые фигуры имеют несколько осей симметрии. Например круг симметричен относительно любой прямой проходящей через его центр перегибание чертежа по диаметру начерченного круга можно убедиться в том, что две части круга совпадают. Поэтому любой диаметр лежит на оси симметрии круга. Докажем этот факт.
Теорема. Окружность симметрична относительно любой прямой, проходящей через ее центр.
Доказательство. Рассмотрим осевую симметрию относительно оси, проходящей через центр О окружности.
Осевая симметрия перемещения (она сохраняет расстояния), поэтому она отображает окружность на окружность того же радиуса. Но центр О данной окружности принадлежит оси симметрии и отображается на себя, поэтому и окружность симметрии Sl отображается на себя.
Отрезок имеет две оси симметрии: он симметричен относительно перпендикулярной к нему прямой, проходящей через его середину, и относительно прямой, на которой этот отрезок лежит .
В дальнейшем чаще всего мы будем иметь дело с тремя типами элементов симметрии: плоскость, оси, и центр. Для полноты картины следует, однако упомянуть и еще об одном типе элементов симметрии, а именно о так называемых «сложных» или инверсионных» осях сейчас нам важно отметить что и центр и плоскость симметрии могут рассматриваться как частные случаи инверсионных осей. Центр симметрии является инверсионной осью первого порядка, а плоскость - инверсионной осью 2-го порядка.
Итак мы познакомились с исчерпывающим перечнем элементов конечной симметрии. В нашем распоряжении имеется полный набор разных элементов симметрии для конечных фигур. Для полной характеристики таких фигур необходимо учитывать совокупности всех элементов симметрии, присутствующих на данном объекте.
1. Форма и симметрия растений
Не углубляясь в таинственные области мельчайших частиц, мы пока ограничимся внешними контурами, улавливающими в большинстве случаев. Прежние наблюдения, дополненными симметрии (как классической так и основной) открывают пути к пониманию обобщающих геометрических законов морфологии растений.
С самого начала вспомним, что растения получают питательный материал из воздуха, из воды и почвы усваивая его с помощью солнечной энергии поглощающая поверхность листьев и корней должна быть достаточно велика чтобы уловить необходимое количество пищи. Эта цель достигается не только формой листьев, но и обильным ветвлением побегов и придаточных корней как бы тянущихся во все стороны за питанием. Растение, со всех сторон окруженное однородной питающей средой и не испытывающее на себе определенно направленного действия земного тяготения, должно было бы приобрести форму шара с соответственной симметрией &L & &PC (где Р – плоскость симметрии) подобные формы наблюдаются у некоторых водорослей плавающих во взвешенном состоянии внутри водоемов.
Передо мной стоит задача: по возможности подробнее ознакомиться с отдельными частями растений и применить с начала к ним, а затем и по всему живому царству в целом понятии симметрии, как классические так и новейшие. Речь будет идти преимущественно о семенных (цветковых) растениях. Прежде всего, отметим одну из основных особенностей строения семенного растения, а именно его «полярность», которая заключается в ясно выраженном различии между основанием и верхушкой (листа) растения. С точки зрения симметрии полярность может быть охарактеризована вертикальной осью симметрии. L2 совпадающей со стволом или стеблем растения, причем разные концы оси являются неодинаковыми.
Полярность оси исключает возможность существования перпендикулярных к ней плоскостей симметрии и добавочных осей строгого порядка, а также и центра симметрии, здесь могут быть только плоскости симметрии идущие вдоль оси L2 и придающие всему растению радиально-лучевую симметрию типа L2 и Р. Сама ось L2, всесторонне окружена сверху однородной воздушной средой, а снизу – почвой, является в растении главной вертикальной осью симметрии.
Если бы развитие главной оси подчинялось воздействию только окружающей среды, то порядок оси достиг бы бесконечности. Всесторонний подток питания в однородных средах как сверху так и снизу можно уподобить двум полушариям одно из них окружает растение в воздушной среде другое в почве. Симметрия каждого такого полушария L& &P. Она не измениться, если мы учтем воздействие поля земного тяготения то оси симметрии совпадают с вертикальной осью растений.
Нельзя, однако, ограничиваться учетом воздействия лишь внешней среды на формирование растений. Основным фактором такого формирования является внутреннее строение растения со всеми присущими именно ему особенностями. Это строение очевидно, и вызывает формирование осей симметрии различных порядков (3,4,5,6 и т. д. ), совпадающих по направлению с вертикальной осью L& среды.
Открывается среди растений также существуют правши и левши. Мы уже знаем, что правые и левые формы появляются лишь в тех классах симметрии где присутствуют любые инверсионные оси, в том числе плоскости и центр симметрии. Следовательно, оси симметрии растений по самой их природе не должны были бы сопровождаться плоскостями симметрии. Появление таких плоскостей явно называется сильным воздействием поля тяготения и питающей среды с их симметрией L& &P.
Итак, видимые на растениях плоскости симметрии являются ложными и навязанными растению из вне, а не принадлежащими соответственной его симметрии. Очевидно, оси симметрии L& с их левизной или правизной в большинстве случаев принадлежит собственно самим растениям, тогда как присутствующие на растениях видимые плоскости симметрии являются отпечатками симметрии среды.
Приступим теперь к систематическому просмотру отдельных частей растения, при этом обратим сначала внимание на вертикально и наклонно (или горизонтально) расположенные части и на их согласованность с двумя типами симметрии: L& &P и Р. Затем внимательно присмотримся к отклонениям от этих двух типов.
Начнем наш разбор с основания семенного растения, а именно, с его корня. Формы корней, как известно, весьма разнообразны. В большинстве случаев ясно выделяется главный корень имеющий в почве вертикальное направление.
По сторонам главного корня развиваются боковые корни, растущие наклонно или горизонтально. Вертикальное направление посредине главного корня обычно совпадает с осью симметрии, причем зачастую оно приближается к оси L&. Вдоль этой оси пересекаются прослеживаемые на глаз вертикальные плоскости симметрии. Поперечные сечения корней со следами их внутреннего строения дают иногда возможность уточнить истинный порядок оси корня. Итак, симметрия правильно развитых корней, не изуродованных каким-либо побочным действием в общем подчиняются симметрии типа LnnP. Тем самым она хорошо согласуется с симметрией питающей среды, находятся в поле земного тяготения (LnnP).
Вместе с тем именно эти малозаметные частности служат вехами на пути к выяснению истинной симметрии природных тел. Это всецело относится и к геометрии растительных корней.
Тщательные исследования боковых корней показало, что их взаиморасположение не подчиняется радиально лучевой симметрии существуют и левые корни, характеризующие наличие вертикальных осей без плоскостей симметрии. Таким образом даже в почве не смотря на сильный отпечаток симметрии наложенный средой LnnP все же заметно проявляется и собственная симметрия корня со своей природной левизной или правизной.
Поднимаемся несколько выше вдоль главной оси растения и рассмотрим его стебель, сначала отдельно, а потом вместе с ответвлениями и листьями. Обычно направление роста стебля вертикальное, но прямо противоположное по отношению направления роста главного корня. Существуют также ребристые многогранные, утолченные стебли и стволы. Так, семейству губоцветных свойственны четырехгранные стебли с симметрией L44P. Утолщенные стебли могут быть охарактеризованы симметрией L22P. Если внимательно присмотреться в расположение листьев вдоль стебля, то правда, в некоторых случаях совокупность листьев не нарушает общей радиальной симметрии. Приведем пример на мутовчатом листорасположении отдельные группы листьев группируются кольцеобразно на одной и той же высоте стебля. Ясно, что такие кольца из истьев совместно со всем стеблем подчиняются симметрии LnnP (при трех листьях кольце L33P).
Природой устремленного в высь растения временно как бы побеждается влияние среды с симметрией L&&P. Ось растения совпадает с осью L& среды, однако ее природная правизна или левизна не согласуется с радиально-лучевым характером этой среды. При торможении или исчезновении трансляции роста, стебель останавливается и листья одного цикла оказываются расположенными вокруг стебля на одной высоте. При этом растение приобретает внешнюю симметрию LnnP, подчиняющуюся симметрии поля земного тяготения.
Переходим к форме листьев в подавляющем большинстве случаев листья могут быть разделены на две более или менее симметричные половинки, следовательно, они обладают более или менее четко выраженной плоскостью симметрии. Ботаники подразделяют листья на простые и сложные. Простые имеют только одну пластинку. По форме пластинок различают овальные, яйцевидные, продолговатые, лучевидные и другие. Формы основания пластинок бывают клиновидные, сердцевидные и т. п. Уже сами эти названия дают понятия о симметрии. Все они обладают одной плоскостью симметрии проходящей вдоль черешка и посередине черешка.
Сложный лист отличается от простого тем, что в его черешке имеется несколько пластинок. Несмотря на их прихотливость и разнообразие, все они также одной более или менее ясно выраженной плоскости симметрии, направленной вдоль линии черешка. Форма листьев одного и того же растения может выигрывать в зависимости от условий питания, освещения, влажности и т. п. Однако симметрия листа упорно стремиться к билатеральной. Этого и следовало ожидать так как листья отклонены от вертикальной оси растения и развиваются, как правило с боку стебля.
Тщательный математический анализ, разработанный Ю. И. Румянцевым и проверенный на огромном природном материале показал, что и листья подразделяются на правшей и левшей. Такая правизна – левизна порождается неравномерным развитием пластинок по разные стороны от «средней» линии.
Поднимаясь вдоль оси растения, мы наконец дошли до ее цветков и соцветий появление цветка на побеге связано с торможением, а затем и прекращением верхушечного роста этого побега.
Хорошо знакомые нам цветы лилии, табака, соцветия подсолнечника, ромашки демонстрируют во всей красе характерную радиально-лучевую симметрию. Цветки с симметрией Lnnp называются параллельными или «актиноморфными» пазушные цветки называются «неправильными или зигоморфными».
Правильные цветки, лепестки которых расположены последовательными концентрическими кругами, называются «круговыми» или «циклическими». При геометрическом анализе таких форм целесообразно использовать понятие симметрия подобия А. В. Шубникова, каждый последующий круг получает здесь из предыдущего с помощью трансляций подобие, идущим по радиусам из центра.
Симметрия плодов с первого взгляда получают симметрию радиально-лучевого типа. Однако исследования Ю. А. Урманцова вносят и сюда соответственные уточнения. Оказывается и на плодах обнаруживаются признаки левизны и правизны в виде скученности, преимущественного развития в одном направление и т. д.
Итак, мы постепенно поднялись от корня до верхушки растения всматриваясь в отдельные его части. Почти всюду с первого взгляда подтверждается общее правило: вертикальные части подчиняются конечной симметрии типа LnnP, а боковые обнаруживают симметрию Р.
Вместе с тем при более тщательных исследованиях обнаруживаются следы собственной симметрии растений с их правизной и левизной, не подчиняющимся симметрии среды.
В нашем анализе симметрии растительных форм были по отдельности рассмотрены корни, стебли, листья, цветы, плоды. Далее хотелось бы объединить все эти детали в стройное целое и уловит те обобщающие законы которые связывают их между собой. Здесь нам на помощь приходит великий поэт-натуралист Гете, открывший явление «метаморфоза растений». В стихотворении, посвященном этому открытию он пишет:
В каждом цветочке есть сходство с другими,
Но есть и различия
Ясно, что в целом скрыт дивный
Могучий закон
В чем же заключается этот замечательный закон все части растения представляют только преемственные метаморфозы одного и того же элементарного члена.
Стройным, красивым колечком
Становятся листья-малютки
Или в числе небольшом,
Или без счету вокруг
Внешние чашечкой станут
Цветочную ось окруживши
Внутренний ряд лепестков венчик
Роскошный родит.
Ныне блистает растение
Полной своей красотою
Члены за членами в нем
Стройном порядке идут
Сочными листьями стебель покрыт
И пышно качаясь
Дивно-прекрасный цветок
Гордо венчает его.
В самом деле, «метаморфоза» Гете – это обобщенная картина живой динамической симметрии растений, требующая своего окончательного оформления в виде стройного геометрического закона.
II. Практическая часть
2. 1. Особенности каждого типа симметрии
Из теоретической части мы узнали, что два вида симметрии с необычным упорством повторяются вокруг нас. И я в этом убедилась на собственном опыте.
Однажды летом, когда я ездила на юг я побывала в парке, где меня окружали различные цветы, деревья.
Подул ветерок и листок с дерева упал мне прямо на рукав. Форма его не является случайной, она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок. Одна из этих половинок расположена зеркально относительно другой, совсем так, как располагаются друг относительно друга отражение какого- либо предмета в зеркале и сам предмет. Чтобы убедиться в этом, я поставила карманное зеркальце с прямым краем на линию, идущую вдоль черенка и разделяющую пластинку листа пополам. Заглянув в зеркальце, я увидела, что отражение правой половины листа более или менее точно заменяет его левую половину и, наоборот, левая половина листка в зеркальце как бы перемещается на место правой половины.
Плоскость, разделяющая листок на две зеркально равные части (которая сейчас совпадает с плоскостью зеркала), называется «плоскостью симметрии». Ботаники и зоологи называют такую симметрию билатеральной (в переводе с латинского дважды боковой).
Только ли древесный листок обладает такой симметрией? Нет. Пройдя зону растений в парке нас привели прямо к озеру, где плавали белые лебеди Мы и лебедя можем мысленно разделить вдоль на две зеркально равные части.
Если посмотреть на красавицу бабочку с яркой расцветкой. Она тоже состоит из двух одинаковых половинок. Даже пятнистый узор на ее крыльях подчиняется такой геометрии
И выглянувший из травы жучок, и промелькнувшая мошка, и сорванная ветка, - все подчиняется «билатеральной симметрии». Итак, повсюду в лесу мы наталкиваемся на билатеральную симметрию. Может быть любое существо обладает плоскостью симметрии и следовательно, подходит тем самым под билатеральную симметрию.
На первый взгляд может показаться, что подходит, но не все так просто, как кажется. Возле куста скромно выглядывает из травы обыкновенный поповник (ромашка). Я сорвала его и рассмотрела. Вокруг оранжевой середки, как лучи вокруг солнышка на детском рисунке, расположены белые лепестки.
Имеет ли такое «цветочное солнышко» плоскость симметрии? Конечно! Без всякого труда можно его разрезать на две зеркально равные половинки по линии, проходящей через центр цветка и продолжающейся воль середины любого из лепестков или между ними. Это, однако, не все. Ведь лепестков то много и вдоль каждого лепестка можно обнаружить плоскость симметрии. Значит, этот цветок обладает многими плоскостями симметрии, и все они пересекаются в его центре. Сходным образом, можно охватить и геометрию подсолнечника, василька, колокольчика.
Но когда я пришла после прогулки у дома, где мы проживали, я увидела красиво лакированный деревянный грибок с нарядной красной шляпкой и желтой ножкой. Легко понять, что вдоль ножки и через середину шляпки можно провести бесчисленное множество плоскостей симметрии. Все они пересекаются в центре шляпки, образуя веер плоскостей.
Все то, что растет и движется по вертикали ,то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой симметрии в виде веера пересекающихся плоскостей симметрии. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии.
Этому всеобщему закону послушны не только цветы, животные, легкоподвижные жидкости и газы, но и твердые неподатливые камни, и изменчивые формы облаков.
2. Обоснование причин симметрии у растений.
Мною была проведена исследовательская работа, цель которой выяснить причины, обусловливающие симметрию в царстве растений. В две прозрачные трубки я поместила проростки бобов. Одну трубку расположила в горизонтальном положении, а другую в вертикальном. Через неделю обнаружила, что, как только корень и стебель выросли за пределы горизонтально расположенной трубки, корень стал расти строго вниз, а стебель вверх. Я считаю, что рост корня вниз обусловлен земным притяжением; рост стебля вверх – влиянием света. Опыты, проводимые космонавтами на борту орбитальной станции в условиях невесомости, показали, что при отсутствии силы тяжести привычная пространственная ориентация у проростков нарушается. Следовательно, в условиях земного притяжения наличие симметрии позволяет растениям занять устойчивое положение.
Вывод: Чаще всего центральная симметрия встречается у цветковых и у голосеменных в листьях. У осевой симметрии наибольшее количество растений это водоросли корень и листья), зеленые мхи (корень, стебель, листья), хвощи (корень, стебель, листья), плауны (корень, стебель, листья), папоротники (корень, листья), голосеменные и цветковые. У зеркальной симметрии встречаются такие виды растений, как плауны (стебель ,листья ), папоротники (листья), голосеменные (стебель, плоды ) и цветковые.
Что же является основной причиной возникновения различной симметрии у растений?
С точки зрения физики – сила тяжести.
Каково значение использования знаний из курса геометрии и физики в биологии?
Данные предметы помогают выяснить причины симметрии в природе, определить тип симметрии у любого растения.
Заключение
Трудно найти человека, который не имел бы какого-либо представления о симметрии, которая объясняет наличие определенного порядка, закономерность в расположении частей чего-либо. В каждом цветочке есть сходство с другими, но есть и различие.
Ясно, что в целом скрыт дивный
Могучий закон.
Стройным красивым колечком
Становятся листья-малютки
Или в числе небольшом,
Или без счету вокруг
Внешние чашечкой станут,
Цветочную ось окруживши
Внутренний ряд лепестков венчик
Роскошный родит.
Ныне блистает растение
Полной своей красотою.
Члены за членами в нем
Стройном порядке идут,
Сочными листьями стебель покрыт
И пышно качаясь
Дивно-прекрасный цветок
Гордо венчает его.
Эта обобщенная картина живой динамической симметрии растений, требующая своего окончательного оформления в виде стройного геометрического закона.
Преодолев и продумав все изложенное на страницах моего проекта, я теперь могу утверждать; все что растет по вертикали ,то есть вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой симметрии в виде веера пересекающихся плоскостей симметрии; все то что растет горизонтально или наклонно по отношению к земной поверхности подчиняется билатеральной симметрии. Так же я на практике доказала, что упорядоченность и пропорциональность растений обусловлена двумя факторами;
-земное притяжение;
-влияние света.
Выяснить причины симметрии в природе и определить тип симметрии у растений мне помогли знания из курса геометрии и физики.
Знание геометрических законов природы имеют огромное практическое значение. Мы должны не только научиться понимать эти законы, но и заставлять служить нам на пользую
О симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан и роза
И снежный рай – творение мороза.
www.hintfox.com
СИММЕТРИЯ ЦВЕТКА И СТРОЕНИЕ ЛЕПЕСТКОВ
Здравствуйте, друзья!
В преддверии 8 марта хочется говорить о прекрасном, о женщинах, о цветах. Поздравляю с весенним праздником, пусть весна окрыляет творчеством и красотой! И каждый день будет прожит с любовью и радостью. Продолжаю цикл статей о цветке и его строении. Речь пойдет о самой красивой части цветка - о венчике. С ботанической точки зрения, венчик - это внутренняя часть двойного околоцветника. Предлагаю посмотреть на подаренный букет на 8 марта под новым углом. А из лепестков сделать гербарий.
Почему лепесток так назвали?
Лепестки образовывались из стерильных тычинок, реже из листьев. Свое название "лепесток" получил от старинного слова "лепест", так на Руси ласково величали листочек. Но я подозреваю, что название пошло также от слова "лепый" - красивый. Есть еще одно редко употребляемое и трудно произносимое название - венцелистик. Как думаете, почему ему присудили такое название? КТО В ЦВЕТКЕ КОРОЛЬ?(автор: Астраханцева О.А.) Называют лепестокВенцелистиком, дружок.Носит он свою корону,Но корона из картона. Кто же настоящий царь?Кто цветочный государь?Это пестик и тычинки,Что сидят по серединке.Венцелистик означает венценосный, королевский, царствующий листок. Лепестки самые заметные. Они нужны для привлечения внимания опылителей. Но истинные короли в цветке - пестик и тычинки.Строение и типы лепестков
Лепестков в венчике бывает от 1-2 до 120 и более у махровых форм. Но чаще всего количество лепестков фиксированное. Наиболее популярное число лепестков в цветках - 3, 4, 5 и 6.Лепестки содержат в себе воздушные полости, а их клетки богаты вакуолями с пигментами, придающими окраску. Если посмотрим лепестки на просвет, то заметим в них жилки-трубочки. По ним лепестки получают питание и воду. По серединке лепестка проходит главная жилка, она более заметная.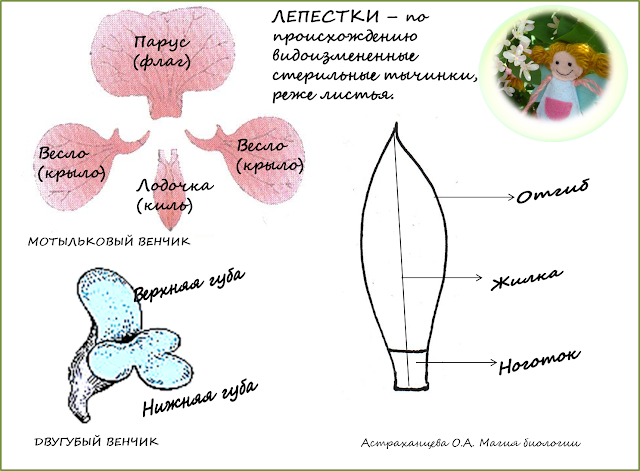
В классическом лепестке выделяют широкую часть - отгиб, и узкую часть - ноготок. Ноготок бывает длинным или коротким. Развитым ноготком обладают лепестки растений из семейства крестоцветных - капуста, горчица. ЗАГАДКА О МЯТЕ (автор: Астраханцева О.А.) Сидит пряный Федул,Сразу две губы надул.Кто его сорвет,Свежий запах обретет.В некоторых венчиках лепестки настолько своеобразные, что им дают собственные названия. В венчике мяты, шалфея. базилика лепестки срослись особым образом и образовали верхнюю и нижнюю губу. ЗАГАДКА О ВЕНЧИКЕ ГОРОХА(автор: Астраханцева О.А.) Что за лодочка такая?Парус флагом подняла.Слева, справа загребают,Словно крылья, два весла.Это лодка не плывет,А в саду моем растет! А у бобовых растений лепестки имеют даже по два имени (см. схему выше). Верхний большой лепесток называется парусом или флагом, боковые - веслами или крыльями, а нижний лепесток срастается, образуя лодочку или киль. Такой венчик называют мотыльковым. Кстати, раннее название семейства бобовых растений - мотыльковые.
Флаги бывают не только у мотыльковых. У ирисов венчиковый околоцветник. Его лепестки организованы в два круга - доли. Верхняя доля поднята как знамёна на параде, поэтому ее части называются флагами, или штандартами (стандартами). Три части нижней доли отогнуты вниз, их называют фолы (фолсы). Фолы имеют бородку - дорожку из волосков, которая указывает насекомым путь к нектару. Фолы - маленькие аэродромы для насекомых. Симметрия цветка
С венчиком связывают еще одно важное понятие - симметрия цветка. С тем, сколько плоскостей симметрии мы можем провести в нём. Две и более плоскостей симметрии имеет правильный (актиноморфный) цветок. Таковы цветки гвоздики травянки, флокса, табака душистого, ночной красавицы.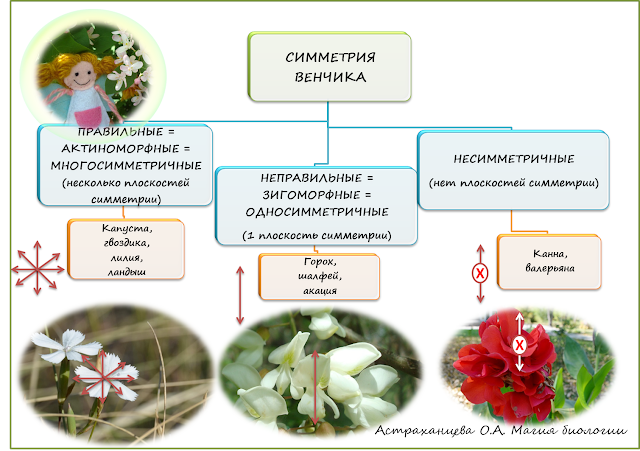
Всего одну плоскость симметрии имеет неправильный (зигоморфный) цветок. Характерен для цветков фасоли, робинии, акации, мяты.А некоторые цветки, и вовсе обходятся без симметрии (ассиметричные). Например, у канны и валерьяны. Биологическая игра с зеркалом "Определение симметрии цветка"
В детстве у сына были книжки-игры издательства "Карапуз" про Алису в Зазеркалье и Карлике Носе. К ним прилагалось гибкое зеркало из фольги, прислоняя, которое к иллюстрациям, можно было за счет симметрии находить новые образы. Например, превратить кошку в сову. Она была построена на игре всего с одной плоскостью симметрии. И я подумала, что также можно поиграть и с венчиками цветков. Приглашаю взять зеркальце (прямоугольной формы без ободка) и отправиться изучать цветки на клумбу в игре. Такое зеркало можно извлечь из коробочки с пудрой. Вместо зеркала для малышей можно взять гибкую фольгу в целях безопасности. Изображение немного потеряет в четкости, но симметрию можно будет определить. У гибкой фольги есть еще один плюс - ею можно тестировать даже мелкие цветки. |
| На фото показана симметрия цветка кислицы треугольной с помощью гибкого зеркала из фольги. |
Отражение симметрично?Встреча ждет с цветком приличным.И в канонах знает толк,Этот ПРАВИЛЬНЫЙ цветок.С симметричностью на ты,Все послушные цветы. 
А у этого цветка -Очень странные бока.Ставим зеркало хоть как,Нет симметрии никак.Твоего знакомства личноЖдет цветок АССИМЕТРИЧНЫЙ. 
Задания для дневника исследования
Феечки спешат с новыми заданиями для юных исследователей - взять зеркальце и провести исследование на предмет симметрии цветков в своем саду, на подоконнике или на городской клумбе. 1. Создайте подборку фотографий правильных, неправильных и асимметричных цветков, растущих в вашем саду или в парке. 2. Проведите исследование. Подсчитайте количество правильных, неправильных и асимметричных. Подумайте, с чем могут быть связаны эти различия в количествах. Какая симметрия была первичной, а какая появилась позже? |
| На венчике ядовитого растения белены видны фиолетовые жилки. Пахнет белена неприятно, поэтому животные обходят его стороной. Растение не стоит трогать руками, но сфотографировать для коллекции можно. |
 |
Черная белена растение ядовитое, с ним нужно быть осторожным. |
Зачем морознику яркие чашелистики
ПС: В предыдущем выпуске шла речь о чашечке, выполняющей роль венчика у морозника. Феечки задали вопрос о том, зачем морознику яркие чашелистики, если он зацветает, когда еще не проснулись насекомые? Спасибо Марине за участие в обсуждении, она выдвинула версию очень близкую к моей."Марина: А морозник такой яркий может потому, чтобы привлечь солнышко, чтоб его сильнее согревало, а заодно и те немногие насекомые, которые проснулись - чтоб летели на него согреться, перекусить, ну и опылить заодно?"Да, все же отдельные опылители, выбираются из своих укрытий под дневное солнышко. Морозник цветет тогда, когда у него нет никакой конкуренции среди первоцветов. Крапивница может вылететь и при +10 градусах, и шмели просыпаются и жужжалы. Их-то и ждет морозник, для них готовит нектар.
Но на случай, если не дождется гостей, у него припасено опыление с помощью ветра. Но лучшие жизнеспособные семена получаются от опыления насекомыми.
Хотя, у меня есть еще одна гипотеза, почему чашелистики морозника преобразуются в нежные лепестки. Это наличие воздушных полостей. Воздух замечательно сохраняет тепло, чем и пользуются производители пуховиков, наполняя их синтепоном.
В следующий раз поговорим о типах венчика.Если Вам понравилось, расскажите друзьям о блоге "Магия биологии". Пусть неравнодушных к живой природе людей будет больше.
Желаю Вам радости открытий!
biomagic27.blogspot.ru
Симметрия у растений и её виды | Биология. Реферат, доклад, сообщение, краткое содержание, лекция, шпаргалка, конспект, ГДЗ, тест
Тело растений состоит из клеток, а среди низших растений — бактерий, водорослей, грибов — мы встречаем растения, все тело которых состоит из одной клетки (одноклеточные). Интересно поэтому на этих простейших растениях проследить, какие явления симметрии мы можем встретить среди них. Особенно хорошо явления симметрии выражены у высших растений.
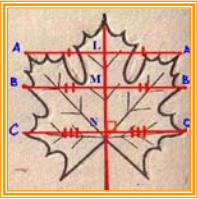
На рисунке 0 изображена микроскопическая сине-зеленая водоросль Chroococcus. Все тело этой одноклеточной водоросли снаружи имеет форму шара. Организм этот представляет собой тело, через которое можно провести по крайней мере три взаимно перпендикулярные оси, притом одинаковой длины, т. е. он характеризуется наивысшей степенью симметрии, где осей симметрии и плоскостей симметрии бесконечное множество. Такое строение называется полисимметрическим или радиальным. У высших растений примером полисимметрического строения могут служить венчики многих цветков, например мака, шиповника, первоцвета, гвоздики и др.; стебли с супротивно сидящими листьями, например у губоцветных (глухая крапива, мята), цилиндрические стебли кактусов.
 |
| Рис. 0. Сине-зеленая водоросль Хроококк (Chroococcus) |
Рисунок 1, 1 представляет одноклеточную водоросль Micrasterias из семейства десмидиевых — микроскопических форм, водящихся в торфяных болотах. Водоросль эта имеет плоскую форму и состоит из симметричных половинок, соединенных друг с другом небольшим перехватом. Micrasterias имеет только две плоскости симметрии. Такое строение называется бисимметрическим или билатеральным. У высших растений билатеральное строение имеют, например, плоские стебли кактуса опунции (Opuntia) (рис. 1,4), стебли с двурядным расположением листьев (например, у злаков).
Если обратимся теперь к рисунку 1, 2, изображающему одноклеточную водоросль из рода Chlamydomonas, то здесь возможно будет провести только одну продольную плоскость симметрии. Такое строение называют моносимметрическим. У многих высших растений цветки моносимметричны: например у анютиных глазок (Viola) (рис. 1, 5), гороха, глухой крапивы. Точно так же листья многих растений, например злаков, ландыша и др., которые могут быть разделены на правую и левую одинаковые части, будут моносимметричными.
Приведенные примеры явлений симметрии показывают нам, что даже у разных одноклеточных растений тело развито неодинаково в разных направлениях. Различают еще асимметричное строение, когда через тело растения или его орган нельзя провести ни одной плоскости симметрии. Примером может служить неравнобокий лист вяза (рис. 2, 1). Асимметричным является цветок валерианы (рис. 2, 2), канны.
При различии верхней и нижней поверхности (во внешнем и внутреннем строении), говорят о дорзовентральном, или спиннобрюшном, строении (дорзум — спина, вентер — брюхо). Дорзовентральное строение имеет лист, если он растет более или менее горизонтально (рис. 2, 3), слоевище маршанции (рис. 2, 4) и других печеночников, как талломных (слоевищных), так и листостебельных. Материал с сайта http://worldofschool.ru
 |
| Рис. 1. Симметрия у растений: 1. Одноклеточная десмидиевая водоросль микрастериас (Micrasterias): бисимметрическое строение. 2. Одноклеточная зеленая водоросль хламидомонада (Chlamydomonas): моносимметрическое строение. 3. Полисимметрический цветок. 4 Билатеральное строение. Плоский стебель (кладодий) кактуса Opuntia. 5. Моносимметрический цветок анютиных глазок (Viola) |
 |
| Рис. 2. Симметрия у растений. Асимметрическое строение: 1 — листа вяза (Ulmus), 2 — цветка валерианы (Valeriana). Дорзовентральное строение: 3 — листа, 4 — слоевища маршанции |
На этой странице материал по темам: Симметрия ландыша
Симметрия морфология растений
worldofschool.ru
12 растений с идеальной симметрией
Природа на столько совершенна, что порой она превосходит саму себя, создавая идеальную симметрию своих творений. Идеальная симметрия в природе встречаются не так уж часто, но на примере растений её всё таки можно наблюдать. На радость перфекционистам представляем 12 растений с идеальной симметрией:
Алоэ многолистное
Романеско
Георгина
Крассула храм будды
Растение Jeweled Carpet (Украшенный Драгоценными Камнями Ковёр)
Лист виктории амазонской
Хойя
Подсолнечник
Камелия
Суккуленты
Людвигия седиоидес
Росолист (Drosophyllum lusitanicum)
Не пропустите интересные новости в фотографиях:
12millionov.com
§ 3. Симметрия в природе
Симметрией обладают объекты и явления живой природы. Она позволяет живым организмам лучше приспособиться к среде обитания и просто выжить.
В живой природе огромное большинство живых организмов обнаруживает различные виды симметрий (формы, подобия, относительного расположения). Причем организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.
Внешняя симметрия может выступить в качестве основания классификации организмов (сферическая, радиальная, осевая и т.д.) Микроорганизмы, живущие в условиях слабого воздействия гравитации, имеют ярко выраженную симметрию формы.
На явления симметрии в живой природе обратили внимание ещё в Древней Греции пифагорейцы в связи с развитием учения о гармонии (V век до н.э.). В XIX веке появились единичные работы, посвящённые симметрии в растительном и животном мире.
В XX веке усилиями российских учёных – В Беклемишева, В. Вернадского, В Алпатова, Г. Гаузе – было создано новое направление в учении о симметрии – биосимметрика, которое, исследуя симметрии биоструктур на молекулярном и надмолекулярном уровнях, позволяет заранее определить возможные варианты симметрии в биообъектах, строго описывать внешнюю форму и внутреннее строение любых организмов.
Симметрия у растений
Специфика строения растений и животных определяется особенностями среды обитания, к которой они приспосабливаются, особенностями их образа жизни.
Для растений характерна симметрия конуса, которая хорошо видна на примере любого дерева. У любого дерева есть основание и вершина, "верх" и "низ", выполняющие разные функции. Значимость различия верхней и нижней частей, а также направление силы тяжести определяют вертикальную ориентацию поворотной оси "древесного конуса" и плоскостей симметрии. Дерево поглощает из почвы влагу и питательные вещества за счёт корневой системы, то есть внизу, а остальные жизненно важные функции выполняются кроной, то есть наверху. Поэтому направления "вверх" и "вниз" для дерева, существенно различны. А направления в плоскости, перпендикулярной к вертикали, для дерева фактически неразличимы: по всем этим направлениям к дереву в равной мере поступают воздух, свет, и влага. В результате появляется вертикальная поворотная ось и вертикальная плоскость симметрии.
У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей. Цветки, имея парные части, считаются цветками с двойной симметрией и т.д. Тройная симметрия обычна для однодольных растений, пятерная – для двудольных.
Для листьев характерна зеркальная симметрия. Эта же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, рябины). Интересно, что в цветочном мире наиболее распространена поворотная симметрия 5-го порядка, которая принципиально невозможна в периодических структурах неживой природы. Этот факт академик Н. Белов объясняет тем, что ось 5-го порядка – своеобразный инструмент борьбы за существование, "страховка против окаменения, кристаллизации, первым шагом которой была бы их поимка решеткой". Действительно, живой организм не имеет кристаллического строения в том смысле, что даже отдельные его органы не обладают пространственной решеткой. Однако упорядоченные структуры в ней представлены очень широко.
Симметрия у животных
Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.
Сферическая симметрия имеет место у радиолярий и солнечников, тела которых сферической формы, а части распределены вокруг центра сферы и отходят от неё. У таких организмов нет ни передней, ни задней, ни боковых частей тела, любая плоскость, проведённая через центр, делит животное на одинаковые половинки.
При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Это кишечнополостные, иглокожие, морские звёзды.
При зеркальной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны – брюшная и спинная – друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих.
Для насекомых, рыб, птиц, животных характерно несовместимое с поворотной симметрией различие между направлениями «вперед» и «назад». Придуманный в известной сказке о докторе Айболите фантастический Тянитолкай представляется совершенно невероятным существом, поскольку у него симметричны передняя и задняя половины. Направление движения является принципиально выделенным направлением, относительно которого нет симметрии у любого насекомого, любой рыбы или птицы, любого животного. В этом направлении животное устремляется за пищей, в этом же направлении оно спасается от преследователей.
Кроме направления движения, симметрию живых существ определяет еще одно направление – направление силы тяжести. Оба направления существенны; они задают плоскость симметрии живого существа.
Билатеральная (зеркальная) симметрия – характерная симметрия всех представителей животного мира. Эта симметрия хорошо видна у бабочки; симметрия левого и правого проявляется здесь с почти математической строгостью. Можно сказать, что каждое животное (а также насекомое, рыба, птица) состоит из двух энантиоморфов – правой и левой половин. Энантиоморфами являются также парные детали, одна из которых попадает в правую, а другая в левую половину тела животного. Так, энантиоморфами являются правое и левое ухо, правый и левый глаз, правый и левый рог и т.д. Симметрия у человека
Человеческое тело обладает билатеральной симметрией (внешний облик и строение скелета). Эта симметрия всегда являлась и является основным источником нашего эстетического восхищения хорошо сложенным человеческим телом. Тело человека построено по принципу двусторонней симметрии.
Большинство из нас рассматривает мозг как единую структуру, в действительности он разделён на две половины. Эти две части – два полушария – плотно прилегают друг к другу. В полном соответствии с общей симметрией тела человека каждое полушарие представляет собой почти точное зеркальное отображение другого
Управление основными движениями тела человека и его сенсорными функциями равномерно распределено между двумя полушариями мозга. Левое полушарие контролирует правую сторону мозга, а правое - левую сторону.
Физическая симметрия тела и мозга не означает, что правая сторона и левая равноценны во всех отношениях. Достаточно обратить внимание на действия наших рук, чтобы увидеть начальные признаки функциональной симметрии. Лишь немногие люди одинаково владеют обеими руками; большинство же имеет ведущую руку.
studfiles.net
