Повторные независимые испытания. Всхожесть партии семян некоторого растения составляет 90
Повторные независимые испытания
⇐ ПредыдущаяСтр 9 из 15Следующая ⇒Программные вопросы
3 Повторные независимые испытания. Теорема Бернулли.
4 Теорема Пуассона.
5 Локальная теорема Лапласа.
6 Интегральная теорема Лапласа.
Решение типового примера
Пример 12.4.1.Всхожесть семян данной партии равна 90%. Найти вероятность того, что 1) из пяти посеянных семян взойдёт не менее четырёх; 2) из 100 посеянных семян взойдет 85; 3) из 200 посеянных взойдёт не менее 190. 4) Найдите наивероятнейшее число взошедших семян из 20 посеянных.
Решение. 1) Так как вероятность того, что каждое семя прорастёт р=0,9 и семян для опыта отобрано всего 5, то вероятность того, что прорастет к семян из n посеянных можно найти по формуле Бернулли: Рn(к)=Сnк ркqn-к, где q=1-р.
В нашем случае, вероятность того, что прорастёт не менее четырех семян, находим, используя формулу Бернулли: Р5(к≥4)= Р5(4) + Р5(5)=С54 р4q5-4+ +С55 р5q5-5= (0,9)4 (1- 0,9) + (0,9)50,919. Здесь использовано, что Сnк= Сnn-к.
2) Так как число посеянных семян достаточно велико, то здесь необходимо использовать локальную теорему Лапласа, в соответствии с которой Рn(к)= , где , .
Таким образом, Р100(85)= = = = 0,1647=0,0549.
Значения функции находят с учётом того, что она чётная по таблице (см. приложение 1).
3) При достаточно большом числе испытаний вероятность того, что событие появится не менее к1 и не более к2 раз в серии из n независимых испытаний, по интегральной теореме Лапласа: Рn (к1 кк2) Ф(х2) - Ф(х1), где Ф(х)= . Значения функции Ф(х) находятся по таблице (см. приложение 2) с учётом того, что эта функция нечётная и при х> 4 Ф(х)=0,5.
В нашем случае Р200 (190 к200) Ф(4,71) - Ф(-2,35) = 0,5 +0,4906= =0,9906, так как х1=, а х2= .
4) Наивероятнейшее число наступлений события в условиях схемы Бернулли, когда вероятность появления события в каждом испытании одна и та же и равна р, а п – число испытаний, удовлетворяет условию:
, где .
В нашем случае, р=0,9, q=0,1, п=20, и , то есть, , но - целое число. Следовательно, =18.
Ответ: 1) 0,919; 2) 0,0549; 3) 0,9906; 4) 18.
Пример 12.4.2.Вероятность заболевания животного в стаде равна 0,002. Найдите вероятность того, что среди 1000 голов не окажется больных животных.
Решение. Поскольку вероятность заболевания животного в многочисленном стаде мала, для нахождения требуемой вероятности применим теорему Пуассона, по которой , где . В нашем случае п=1000, р=0,0002, k=0 и . Для нахождения используем таблицу (см приложение 3): 0,1353.
Ответ: 0,1353.
Задачи контрольной работы
12.4.1. Доля зараженности зерна вредителями составляет 0,004. Какова вероятность, что в выборке из 1000 зёрен окажется 5 штук зараженных?
12.4.2. Вероятность рождения бычка при отёле коровы равна 0,5. Найти вероятность того, что от 400 коров родится 190 бычков.
12.4.3. Семена некоторой культуры в 1 кг содержат в среднем 3 семени сорняков. Для опытов отвешивается 200г семян. Определить вероятность того, что в них не окажется семян сорняков.
12.4.4. Вероятность неточной сборки прибора равна 0,2. Найти вероятность того, что среди 500 приборов окажется не менее 420 точных.
12.4.5. Вероятность остановки комбайна из-за поломки равна 0,1. Чему равно наивероятнейшее число комбайнов, работающих в поле, если хозяйство имеет 30 комбайнов.
12.4.6. Всхожесть семян груши составляет 70%. Определить вероятность того, что из посаженных четырёх семян взойдут три.
12.4.7. Всхожесть семян пшеницы составляет 85%. Какова вероятность, что из четырех посеянных семян 1) 3 прорастут? 2) не менее трёх прорастёт?
12.7.8. Вероятность поражения земляники серой гнилью равна 0,4. Сколько растений надо взять, чтобы с вероятностью 0,936 можно было утверждать, что выборка содержит хотя бы одно здоровое растение?
12.4.9. Вероятность поражения помидоров фитофторой равна 0,6. Определить вероятность того, что из 100 проверяемых помидоров 55 будет поражено этой болезнью.
12.4.10. Вероятность того, что хотя бы одно из двух семян одной партии взойдёт, равна 0,99. Найти вероятность того, что из пяти семян данной партии взойдет 4.
12.4.11. Нестандартные детали данной партии составляют 8%. Найти вероятность, что из четырёх взятых наугад деталей не менее трёх окажутся стандартными.
12.4.12. На инкубационную закладку поступила партия в количестве 1000 яиц. Вероятность того, что в результате инкубации из яйца вылупится цыплёнок, равна 0,8. Найти наивероятнейшее число вылупившихся цыплят.
12.4.13. Вероятность того, что расход воды в течение дня не превысит норму, равна 0,8. Найти вероятность того, что расход воды будет нормальным в течение 3 из ближайших четырёх дней.
12.4.14. Вероятность поражения яблок паршой равна 0,001. Найти вероятность того, что из 1000 случайно отобранных плодов поражёнными окажутся 2 яблока.
12.4.15. Вероятность изготовления стандартной детали на данном станке равна 0,9. Найти вероятность, что из взятых наугад 300 деталей 250 окажутся стандартными.
12.4.16. Было посажено 400 деревьев. Найти вероятность того, что число прижившихся деревьев составит от 360 до 375, если вероятность приживания отдельного дерева составляет 0,9.
12.4.17. На некотором участке повреждены градом 20% растений. Какова вероятность, что из 100 растений окажутся повреждёнными от 15 до 25 растений?
12.4.18. Птицефабрика поставляет в магазин 90% яиц первой категории. Найти вероятность того, что в партии 10000 яиц число яиц первой категории будет не менее 8900.
12.4.19. Всхожесть семян данной партии равна 90%. Найти вероятность того, что из 100 посеянных взойдёт 95 семян.
12.4.20. Семена пшеницы содержат 0,2% сорняков. Найти вероятность того, что из 1000 семян будет 3 семени сорняков.
Рекомендуемые страницы:
lektsia.com
Вариант 1.
1. В конверте среди 30 фотографий находится одна разыскиваемая. Из конверта наудачу извлекают 10 фотографий. Найти вероятность того, что среди них окажется нужная.
2. Бросаются 2 игральные кости. Найти вероятность того, что на верхних гранях появятся нечетные количества очков.
3. Слово «ПРОГРАММА» разрезано по буквам на карточки. Затем карточки перемешивают и вынимают без возвращения по одной. Найти вероятность того, что карточки в порядке появления образуют а) слово ПРОГРАММА, б) слово РАМА.
4. В урне содержатся 5 черных и 6 белых шаров. Случайным образом вынимают 5 шаров.
Найти вероятность того, что среди них:
а) 3 белых шара;
б) менее трех белых шаров;
в) хотя бы 1 белый шар.
5. Вероятность появления события А в одном испытании равна 0,7. Вычислить вероятности следующих событий:
а) событие А наступит 3 раза в серии из 5 независимых испытаний;
б) событие А наступит не менее 170 и не более 180 раз в серии из 250
независимых испытаний.
6. Всхожесть семян некоторого растения составляет 90%. Найти вероятность того, что из 800
посеянных семян взойдут не менее 700.
7. В первой урне 5 белых и 5 черных шаров, а во второй – 4 белых и 8 черных шаров. Из обеих урн случайным образом вынимают по 2 шара. Найти вероятность того, что все вынутые шары одного цвета.
8. Литье в болванках поступает из двух цехов: 60% из первого цеха и 40% из второго. Литье первого цеха имеет 5% брака, второго – 10% брака. Взятая наудачу болванка оказалась без дефекта. Какова вероятность того, что она изготовлена первым цехом?
9. В квадрат с вершинами (0, 0), (0, 1), (1, 0), (1, 1) наудачу брошена точка
K (a, b ). Найти
вероятностьтого, чтокорниуравнения
x2+ax +b =0
действительны.
10. ДанзаконраспределенияслучайнойвеличиныX :
| X | –2 | 0 | 1 | 3 |
| p | 0,2 | 0,1 | 0,5 | 0,2 |
Найти функцию распределения
F (x ),значение
F (0).Вычислитьвероятностьтого,что
X приметзначениеиз интервала(0;3). Построитьмногоугольникраспределения.
11. ИзвестнафункцияраспределениядискретнойслучайнойвеличиныX :
⎧ 0,x < 2
⎪
F ( x ) = ⎪0,3,2≤x <3
⎨0,5,3≤x < 4
⎪
⎩⎪1,
x ≥ 4.
Задать закон распределения случайной величины X в виде таблицы.
12. Заданзаконраспределениядискретнойслучайнойвеличины:
| X | 120 | 135 | 150 | 165 | 180 |
| p | 0,1 | 0,2 | 0,3 | 0,2 | 0,2 |
Вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение.
13. В баскетбольную корзину бросают мяч до первого попадания. Разрешается сделать не более трех бросков. Составить закон распределения количества выполненных бросков, если вероятность попадания при одном броске равна 0,7. Найти математическое ожидание и дисперсию числа выполненных бросков.
14. Электростанция обслуживает сеть из 2000 ламп, вероятность включения каждой из которых равна 0,8. Какова вероятность того, что число ламп, включенных в сеть вечером, отличается от своего математического ожидания по абсолютной величине не более чем на
50?
15. На телефонной станции неправильное соединение происходит с вероятностью 0,02. Найти вероятность того, что среди 100 соединений произойдет:
а) ровно 2 неправильных соединения;
б) больше трех неправильных соединений.
16. Случайная величина задана функцией плотности распределения
⎧ 0,x <0
⎪
p ( x ) =⎪x ,0≤x <6
⎨3
⎪
⎪⎩0,x ≥6.
Найти функцию распределения
F (x )
случайной величины X . Построить графики
функций
p (x ) и
F (x ). Вычислить для этой случайной величины математическое
ожидание, дисперсию, среднее квадратическое отклонение, моду и медиану.
17. СлучайнаявеличинаX заданафункциейраспределения
⎧0,x <1
F (x )= ⎪a (x −1),1≤x <3
⎨
Найти а) параметр a ;
б) плотность распределения
⎪
⎩
p (x );
1,x ≥3.
в) вероятность того, что в результате одного испытания случайная величина X
приметзначениеиз интервала(2,5;3,5);
г) математическое ожидание и дисперсию этой случайной величины;
д) вероятность того, что в результате 400 независимых испытаний случайная величина X примет 150 раз значение из интервала (2,5;3,5).
18. Случайная величина X распределена равномерно на отрезке [1, 5; 3, 7]. Найти выражения для плотности распределения и функции распределения этой случайной величины. Вычислить математическое ожидание и дисперсию случайной величины X .
19. Случайная величина распределена по показательному закону с параметром 2,4. Записать выражения для плотности распределения и функции распределения этой случайной величины. Построить их графики. Вычислить математическое ожидание и дисперсию случайной величины X .
20. Случайная величина распределена по нормальному закону с параметрами
Найти вероятность того, что эта случайная величина примет значение
а) из промежутка [1; 1,5];
б) меньшее 8;
в) большее6;
г) отличающееся от своего среднего значения по абсолютной величине не более чем на 7.
a =7
иσ=6.
21. Автомат штампует детали. Контролируется длина детали X , которая распределена
нормально с проектной длиной 50. Известно, что σ = 3,6мм. Найти вероятность того, что
длина наудачу взятой детали находится в пределах от 55мм до 68мм.
22. По выборке А решить следующие задачи:
а) составить вариационный ряд, построить полигон и гистограмму;
б) вычислить относительные и накопленные частоты,
в) построить эмпирическую функцию распределения и ее график,
г) вычислить числовые характеристики вариационного ряда: выборочную среднюю, дисперсию, среднее квадратическое отклонение, моду, медиану.
д) при уровне значимости
α=0,05
проверить гипотезу о распределении
Пуассона соответствующей генеральной совокупности.
Выборка А:
| 4 | 4 | 5 | 1 | 2 | 2 |
| 2 | 3 | 2 | 3 | 2 | 5 |
| 0 | 3 | 0 | 1 | 0 | 2 |
| 5 | 0 | 2 | 3 | 2 | 1 |
| 1 | 4 | 2 | 1 | 1 | 1 |
| 1 | 5 | 2 | 5 | 1 | 2 |
| 3 | 1 | 3 | 4 | 3 | 3 |
| 0 | 0 | 2 | 5 | 2 | 4 |
| 2 | 3 | 2 | 5 | 3 | 2 |
| 2 | 1 | 6 | 3 | 5 | 1 |
23. По выборке В решить следующие задачи:
а) составить вариационный ряд,
б) вычислить относительные и накопленные частоты,
в) построить эмпирическую функцию распределения и ее график,
г) вычислить числовые характеристики вариационного ряда: выборочную среднюю, дисперсию, среднее квадратическое отклонение, моду, медиану.
д) при уровне значимости
α=0,05
проверить гипотезу о нормальном
распределении соответствующей генеральной совокупности.
Выборка В:
| 135 | 124 | 137 | 137 | 133 | 126 | 132 | 114 |
| 124 | 117 | 112 | 119 | 132 | 131 | 134 | 121 |
| 132 | 123 | 126 | 125 | 134 | 127 | 127 | 133 |
| 104 | 129 | 128 | 120 | 131 | 130 | 124 | 135 |
| 152 | 121 | 111 | 129 | 120 | 126 | 127 | 131 |
| 134 | 122 | 129 | 125 | 129 | 124 | 135 | 125 |
| 130 | 125 | 115 | 123 | 135 | 135 | 120 | 114 |
| 129 | 131 | 147 | 127 | 132 | 127 | 129 | 115 |
| 120 | 147 | 131 | 132 | 132 | 108 | 126 | 117 |
| 122 | 124 | 132 | 118 | 108 | 134 | 132 | 118 |
studfiles.net
12.4. Повторные независимые испытания Программные вопросы
Повторные независимые испытания. Теорема Бернулли.
Теорема Пуассона.
Локальная теорема Лапласа.
Интегральная теорема Лапласа.
Решение типового примера
Пример 12.4.1. Всхожесть семян данной партии равна 90%. Найти вероятность того, что 1) из пяти посеянных семян взойдёт не менее четырёх; 2) из 100 посеянных семян взойдет 85; 3) из 200 посеянных взойдёт не менее 190. 4) Найдите наивероятнейшее число взошедших семян из 20 посеянных.
Решение.1) Так как вероятность того, что каждое семя прорастёт р=0,9 и семян для опыта отобрано всего 5, то вероятность того, что прорастет к семян изnпосеянных можно найти по формуле Бернулли: Рn(к)=Сnк ркqn-к, гдеq=1-р.
В нашем случае, вероятность того, что прорастёт не менее четырех семян, находим, используя формулу Бернулли: Р5(к≥4)= Р5(4) + Р5(5)=С54 р4q5-4+ +С55 р5q5-5=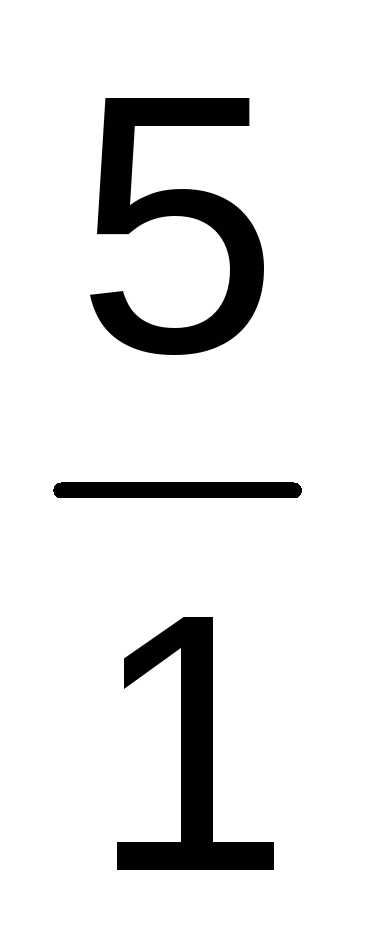 (0,9)4(1- 0,9) + (0,9)5
(0,9)4(1- 0,9) + (0,9)5 0,919. Здесь использовано, что Сnк= Сnn-к.
0,919. Здесь использовано, что Сnк= Сnn-к.
2) Так как число посеянных семян достаточно велико, то здесь необходимо использовать локальную теорему Лапласа, в соответствии с которой Рn(к)=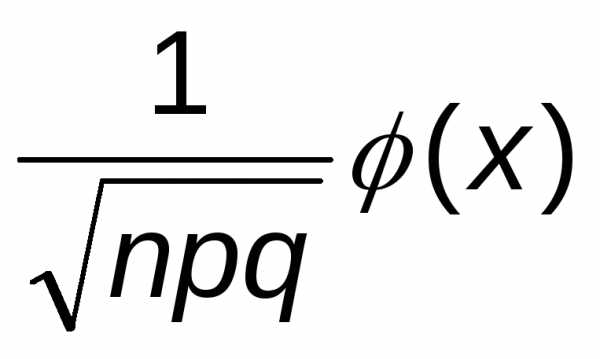 , где
, где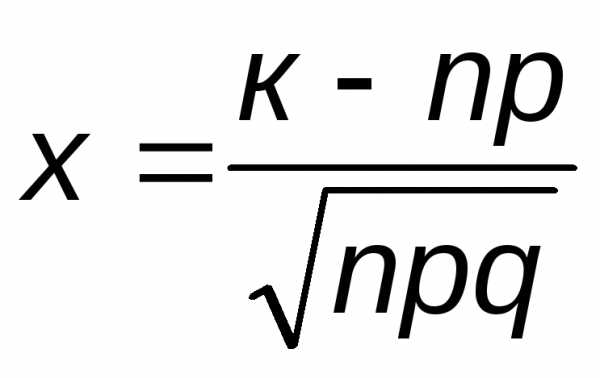 ,
,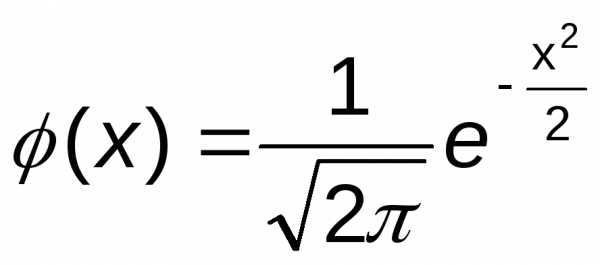 .
.
Таким образом, Р100(85)==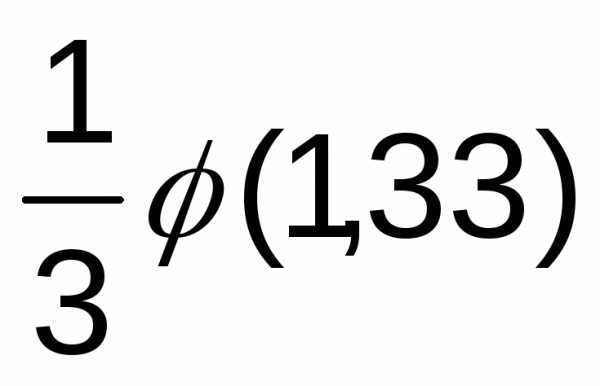 = =
= =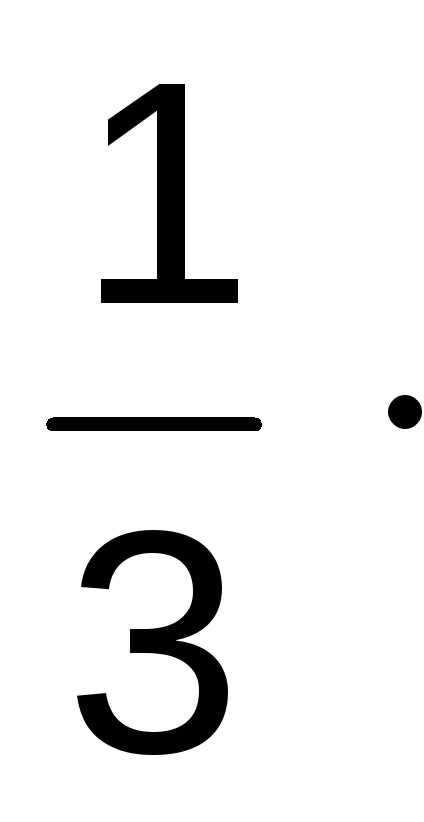 0,1647=0,0549.
0,1647=0,0549.
Значения функции 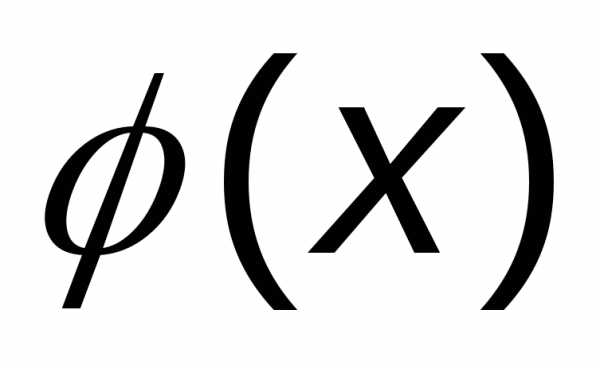 находят с учётом того, что она чётная по таблице (см. приложение 1).
находят с учётом того, что она чётная по таблице (см. приложение 1).
3) При достаточно большом числе испытаний вероятность того, что событие появится не менее к1и не более к2раз в серии изnнезависимых испытаний, по интегральной теореме Лапласа: Рn(к1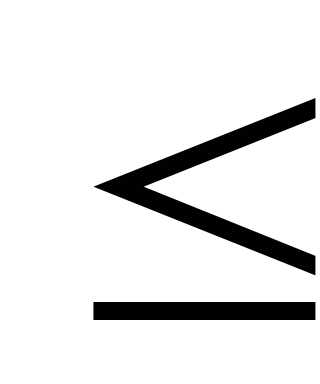 к
к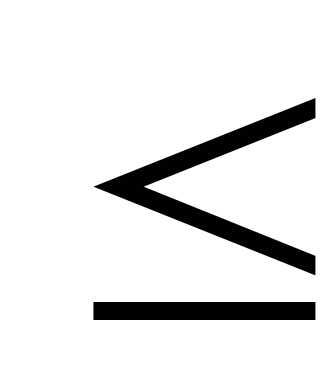 к2)
к2) Ф(х2) - Ф(х1), где Ф(х)=
Ф(х2) - Ф(х1), где Ф(х)=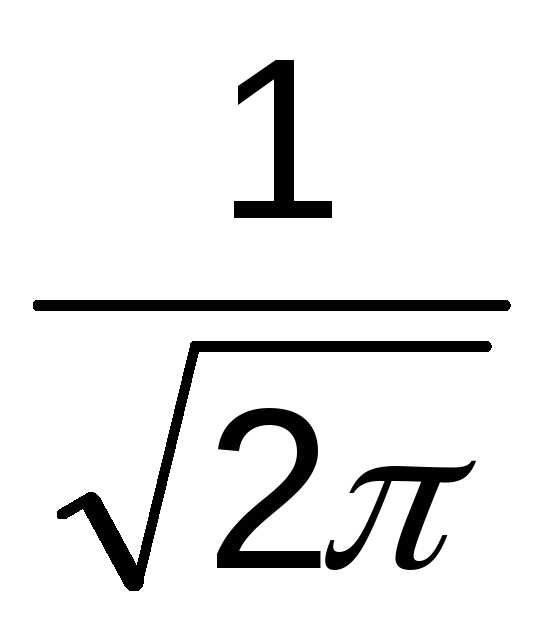
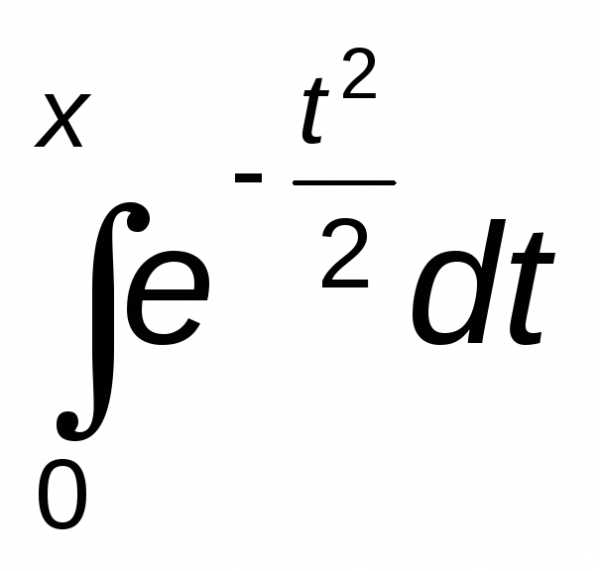 . Значения функции Ф(х) находятся по таблице (см. приложение 2) с учётом того, что эта функция нечётная и при х> 4 Ф(х)=0,5.
. Значения функции Ф(х) находятся по таблице (см. приложение 2) с учётом того, что эта функция нечётная и при х> 4 Ф(х)=0,5.
В нашем случае Р200(190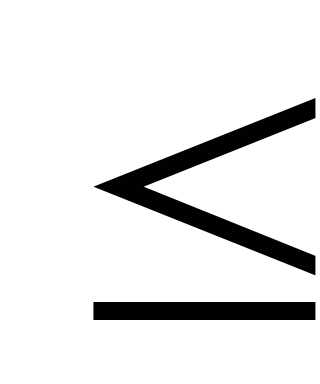 к
к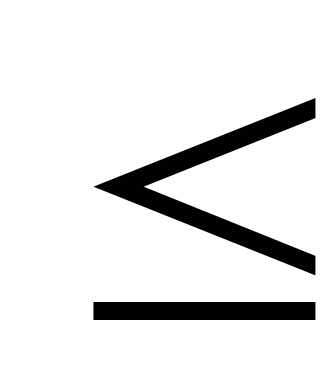 200)
200) Ф(4,71) - Ф(-2,35) = 0,5 +0,4906= =0,9906, так как х1=, а х2=.
Ф(4,71) - Ф(-2,35) = 0,5 +0,4906= =0,9906, так как х1=, а х2=.
4) Наивероятнейшее число 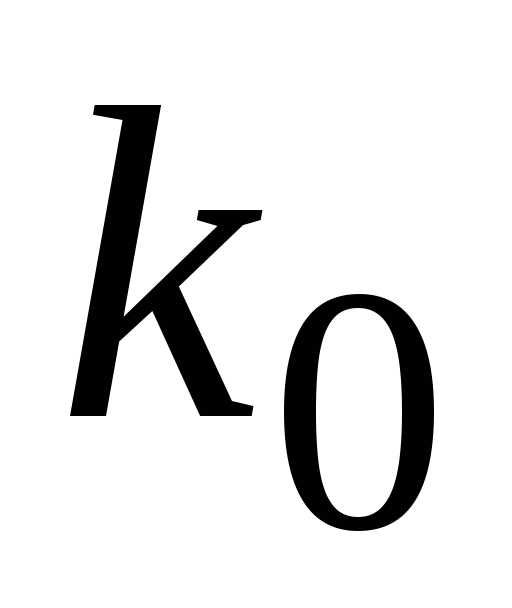 наступлений события в условиях схемы Бернулли, когда вероятность появления события в каждом испытании одна и та же и равнар, ап– число испытаний, удовлетворяет условию:
наступлений события в условиях схемы Бернулли, когда вероятность появления события в каждом испытании одна и та же и равнар, ап– число испытаний, удовлетворяет условию:
, где 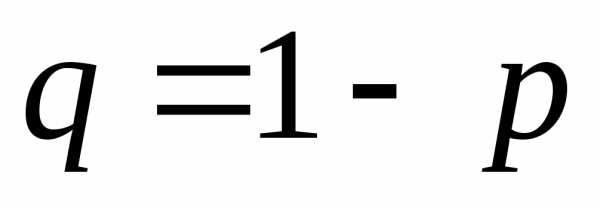 .
.
В нашем случае, р=0,9,q=0,1,п=20, и, то есть,, но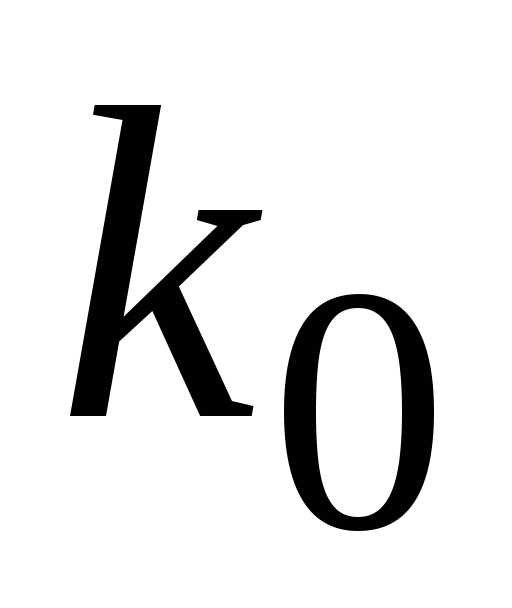 - целое число. Следовательно,
- целое число. Следовательно,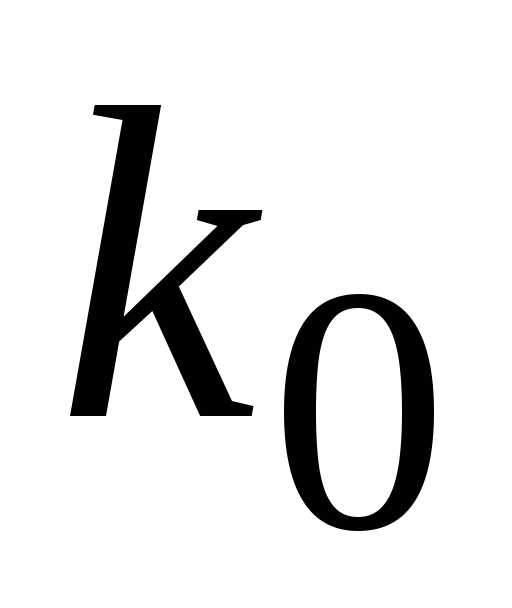 =18.
=18.
Ответ: 1) 0,919; 2) 0,0549; 3) 0,9906; 4) 18.
Пример 12.4.2. Вероятность заболевания животного в стаде равна 0,002. Найдите вероятность того, что среди 1000 голов не окажется больных животных.
Решение.Поскольку вероятность заболевания животного в многочисленном стаде мала, для нахождения требуемой вероятности применим теорему Пуассона, по которой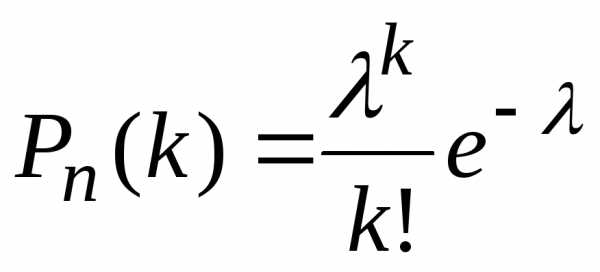 , где
, где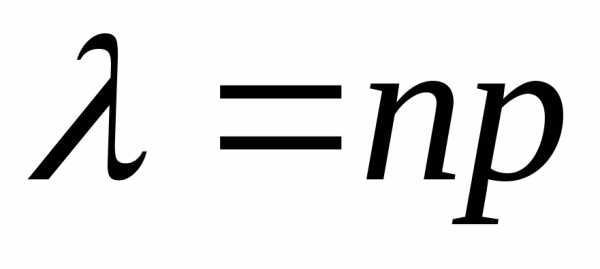 . В нашем случаеп=1000,р=0,0002,k=0 и. Для нахождения используем таблицу (см приложение 3):0,1353.
. В нашем случаеп=1000,р=0,0002,k=0 и. Для нахождения используем таблицу (см приложение 3):0,1353.
Ответ: 0,1353.
Задачи контрольной работы
12.4.1. Доля зараженности зерна вредителями составляет 0,004. Какова вероятность, что в выборке из 1000 зёрен окажется 5 штук зараженных?
12.4.2. Вероятность рождения бычка при отёле коровы равна 0,5. Найти вероятность того, что от 400 коров родится 190 бычков.
12.4.3. Семена некоторой культуры в 1 кг содержат в среднем 3 семени сорняков. Для опытов отвешивается 200г семян. Определить вероятность того, что в них не окажется семян сорняков.
12.4.4. Вероятность неточной сборки прибора равна 0,2. Найти вероятность того, что среди 500 приборов окажется не менее 420 точных.
12.4.5. Вероятность остановки комбайна из-за поломки равна 0,1. Чему равно наивероятнейшее число комбайнов, работающих в поле, если хозяйство имеет 30 комбайнов.
12.4.6. Всхожесть семян груши составляет 70%. Определить вероятность того, что из посаженных четырёх семян взойдут три.
12.4.7. Всхожесть семян пшеницы составляет 85%. Какова вероятность, что из четырех посеянных семян 1) 3 прорастут? 2) не менее трёх прорастёт?
12.7.8. Вероятность поражения земляники серой гнилью равна 0,4. Сколько растений надо взять, чтобы с вероятностью 0,936 можно было утверждать, что выборка содержит хотя бы одно здоровое растение?
12.4.9. Вероятность поражения помидоров фитофторой равна 0,6. Определить вероятность того, что из 100 проверяемых помидоров 55 будет поражено этой болезнью.
12.4.10. Вероятность того, что хотя бы одно из двух семян одной партии взойдёт, равна 0,99. Найти вероятность того, что из пяти семян данной партии взойдет 4.
12.4.11. Нестандартные детали данной партии составляют 8%. Найти вероятность, что из четырёх взятых наугад деталей не менее трёх окажутся стандартными.
12.4.12. На инкубационную закладку поступила партия в количестве 1000 яиц. Вероятность того, что в результате инкубации из яйца вылупится цыплёнок, равна 0,8. Найти наивероятнейшее число вылупившихся цыплят.
12.4.13. Вероятность того, что расход воды в течение дня не превысит норму, равна 0,8. Найти вероятность того, что расход воды будет нормальным в течение 3 из ближайших четырёх дней.
12.4.14. Вероятность поражения яблок паршой равна 0,001. Найти вероятность того, что из 1000 случайно отобранных плодов поражёнными окажутся 2 яблока.
12.4.15. Вероятность изготовления стандартной детали на данном станке равна 0,9. Найти вероятность, что из взятых наугад 300 деталей 250 окажутся стандартными.
12.4.16. Было посажено 400 деревьев. Найти вероятность того, что число прижившихся деревьев составит от 360 до 375, если вероятность приживания отдельного дерева составляет 0,9.
12.4.17. На некотором участке повреждены градом 20% растений. Какова вероятность, что из 100 растений окажутся повреждёнными от 15 до 25 растений?
12.4.18. Птицефабрика поставляет в магазин 90% яиц первой категории. Найти вероятность того, что в партии 10000 яиц число яиц первой категории будет не менее 8900.
12.4.19. Всхожесть семян данной партии равна 90%. Найти вероятность того, что из 100 посеянных взойдёт 95 семян.
12.4.20. Семена пшеницы содержат 0,2% сорняков. Найти вероятность того, что из 1000 семян будет 3 семени сорняков.
studfiles.net
Предельные_Теоремы_Контрольная
Билет №1
1. Случайная величина X задана интегральной функцией:
| 0,x≤ 2 | ||||
|
| 2 |
| ,2 <x ≤4 | |
F( x ) = ( x −2 ) |
| 4 | |||
|
|
|
| ||
1,x> 4 | |||||
| |||||
|
|
|
|
| |
С помощью неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 1;
2.Средний вес клубня картофеля равен 120 г. Какова вероятность того, что наугад взятый клубень картофеля весит не более 300 г?
3.Случайная величина X имеет закон распределения:
хк | 2 | 3 | 4 | 4,5 | 5 | 6 |
|
Pk | 0,1 | 0,4 | 0,3 | 0,05 | 0,05 | 0,1 |
|
|
|
| |||||
Пользуясь неравенством Маркова, оценить вероятность того, что случайная | |||||||
величина X примет значение, большее 4.
4. Всхожесть семян некоторого растения составляет 60%. Найти вероятность того, что при посеве 10000 семян отклонение доли взошедших семян от вероятности того, что взойдет каждое из них, не превосходит 0,01.
Билет №2
1.Случайная величина X задана интегральной функцией
|
| 0,x≤ 0 | |
| 2 |
| ,0 <x ≤4 |
F( x ) = x |
| 16 | |
|
|
| |
| 1,x> 4 | ||
|
| ||
Используя неравенство Чебышева, оцените вероятность того,
что |Х - М(х)|<2 ;
2.Случайная величина X имеет дисперсию DX = 0,01. Какова вероятность того, что случайная величина X отличается от MX =а не более чем на 0,25?
3.Сколько надо произвести измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более чем на 1, если среднее квадратическое отклонение (ошибка измерений) не превосходит 3?
4.Опыт страховой компании показывает, что на каждый пятый договор приходится страховой случай. Сколько договоров нужно заключить, чтобы с вероятностью 0,95 можно было утверждать, что доля страховых случаев отклонится от 0,2 не более чем на 0,05?

Билет №3
1.Случайная величина X задана интегральной функцией:
| 0, x ≤3 | ||||
|
| 2 |
| ,3 < x ≤6 | |
F(x)= (x −3) |
| 9 | |||
|
|
|
| ||
1, x >6 | |||||
| |||||
С помощью неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 1,5 ;
2. Среднее изменение курса акций в течение месяца составляет 0,5%. Оценить вероятность того, что в течение месяца курс акций изменится не более чем на 2%.
Дискретная случайная величина X задана законом распределения:
Xi | 2 | 3 |
| 6 |
| 9 |
|
| |
|
|
|
|
|
|
|
|
|
|
Pi | 0,1 | 0,4 |
| 0,3 |
| 0,2 |
|
| |
|
|
|
|
|
|
|
| ||
Используя | неравенство Чебышева, оцените вероятность того, что | ||||||||
|Х - М(х)| >3. |
|
|
|
|
|
|
| ||
3. Случайная величина задана таблицей: |
|
| |||||||
|
|
|
|
|
|
|
|
|
|
| X | 1 | 2 | 3 |
| 5 | 7 | 8 |
|
|
|
|
|
|
|
|
|
| |
| р | 0,1 | 0,5 | 0,1 | 0,1 | 0,1 | 0,1 |
| |
Пользуясь неравенством Маркова, оцените вероятность того, что случайная величина примет значение не меньше 3.
4. Вероятность того, что акции, переданные на депозит, будут востребованы, равна 0,075. Оценить вероятность того, что из 1000 клиентов от 60 до 90 востребуют свои акции
Билет №4
1. Случайная величина X задана интегральной функцией
|
| 0, x ≤ 0 | |
| 2 |
| ,0 < x ≤ 6 |
F(x)= x |
| 36 | |
|
|
| |
| 1, x > 6 | ||
|
| ||
Используя неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 3;
2.Среднее число клиентов, обслуживаемых банком за день, равно 30. Оценить вероятность того, что в течение дня будет обслужено не более 60 человек.
3.Дискретная случайная величина X задана законом распределения:
Xi | -1 | 0 | 1 | 3 | 5 |
|
|
|
|
|
|
|
|
Pi | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
|
|
|
|
|
|
|
|
Используя | неравенство Чебышева, оцените вероятность того, что | |||||
|Х-М(х)|<2,5.
4. Выборочным способом определяют вес колосьев ячменя. Сколько необходимо отобрать колосьев, чтобы с вероятностью не меньшей 0,99 можно было утверждать, что средний вес случайно отобранных колосьев будет отличаться от среднего веса колосьев во всей партии (принимаемого за математическое ожидание) не более чем на 0,1 г? Установлено, что среднее квадратическое отклонение веса не превышает 0,2 г.
Билет №5
1. Случайная величина X задана интегральной функцией:
| 0, x ≤ 4 | ||||
|
| 2 |
| ,4 < x ≤ 8 | |
F(x)= (x −4) |
| 16 | |||
|
|
|
| ||
1, x > 8 | |||||
| |||||
С помощью неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 2 ;
2.Среднее количество звонков в офис фирмы в течение дня равно 30. Оценить вероятность того, что в течение дня появится более 90 звонков.
3.Сколько раз нужно измерить данную величину, истинное значение которой равно а, чтобы с вероятностью, не меньшей чем 0,95, можно было утверждать, что среднее арифметическое этих измерений отличается от а по модулю меньше чем на 2, если среднее квадратическое отклонение каждого измерения меньше 10.
4Всхожесть семян некоторого растения составляет 90 %. Используя неравенство Чебышева, оцените вероятность того, что из посеянных 5000 семян:а) отклонение доли взошедших семян от постоянной вероятности взойти каждомуиз них не превзойдет по модулю 0,03; б) отклонение числа взошедших семян от математического ожидания не превзойдет по модулю
Билет №6
1.Случайная величина X задана интегральной функцией
|
| 0, x ≤ 0 | |
| 2 |
| ,0 < x ≤ 8 |
F(x)= x |
| 64 | |
|
|
| |
| 1, x > 8 | ||
|
| ||
Используя неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 4 ;
2. Количество электроэнергии, потребляемой поселком в течение суток, является случайной величиной, математическое ожидание которой равно 4 тыс. кВт • ч. Оцените вероятность того, что в ближайшие сутки потребление энергии: а) превысит 8 тыс. кВт • ч.; б) непревысит 6 тыс. кВт • ч.
3. . Электронная система состоит из 45 элементов одинаковой надежности, равной 0,95 за время Т. Найти вероятность того, что доля безотказно работавших элементов в течение времени Т отличается от 0,95 не более чем на 0,1.
4. Выборочным способом определяют вес колосьев ячменя. Сколько необходимо отобрать колосьев, чтобы с вероятностью не меньшей 0,99 можно было утверждать, что средний вес случайно отобранных колосьев будет отличаться от среднего веса колосьев во всей партии (принимаемого за математическое ожидание) не более чем на 0,1 г? Установлено, что среднее квадратическое отклонение веса не превышает 0,2 г.
Билет №7
1. Случайная величина X задана интегральной функцией:
|
| 0, x ≤ 5 | |||
|
| 2 |
| ,5 < x ≤10 | |
F(x)= (x −5) |
| 25 | |||
|
|
|
| ||
1, x >10 | |||||
| |||||
С помощью неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 2,5 ;
2.Количество кормов, расходуемых на ферме крупного рогатого скота в сутки, является случайной величиной, математическое ожидание которой равно 6 т. Оцените вероятность.; того, что в ближайшие сутки расход кормов на ферме превысит 10 т.
3.Вероятность вызревания семян овощной культуры в данной местности составляет 0,8. С помощью неравенства Чебышева оцените вероятность того, что из 1000 растений число растений с вызревшими семенами составит от
750до 850. Определите вероятность попадания случайной величины в заданный интервал.
4.Вероятность того, что в библиотеке будет запрос на газету 1937г. равна
0.03.Количество посетителей библиотеки составляет 3000 человек. Оцените вероятность того, что доля посетителей библиотеки, которым понадобится газета, отклонится меньше, чем на 0.08.
Билет №8
1. Случайная величина X задана интегральной функцией
|
| 0, x ≤ 0 | |
| 2 |
| ,0 < x ≤10 |
F(x)= x |
| 100 | |
|
|
| |
| 1, x >10 | ||
|
| ||
Используя неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 5;
2. Среднее число дождливых дней в году в данном пункте равно 90. Оценить вероятность того, что в этом пункте будет более 150 дождливых дней в году? 3. . В хозяйстве имеется 100 автомобилей. Вероятность безотказной работы каждого из них в течение определенного периода составляет 0,9. С помощью неравенства Чебышева оцените вероятность того, что отклонение числа безотказно работавших автомобилей за определенный период от его математического ожидания не превзойдет по модулю 5.
4. Сколько раз нужно измерить данную величину, истинное значение которой равно а, чтобы с вероятностью, не меньшей чем 0,95, можно было утверждать, что среднее арифметическое этих измерений отличается от а по модулю меньше чем на 2, если среднее квадратическое отклонение каждого измерения меньше 10.
Билет №9
1. Случайная величина X задана интегральной функцией:
| 0, x ≤ 6 | |||
| 2 |
| ,6 < x ≤12 | |
F(x)= (x −6) |
| 36 | ||
|
|
| ||
1, x >12 | ||||
| ||||
С помощью неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 3;
2.Расход технической воды на предприятии составляет 5000 л в день, а средне квадратическое отклонение этой величины не превышает 1000 л. Оценить вероятность того, что расход воды в день не превышает 10000 л.
3.Известно, что Р(| X – МХ| < 0,1) =0,95. В каких пределах находится среднее
квадратическое отклонение σХ?
4. Сколько следует провести независимых испытаний, чтобы вероятность выполнения неравенство |m/n-p|<0,06превысила 0,78, если вероятность появления данного события в отдельном испытании р = 0,7 ?
Билет №10
1. Случайная величина X задана интегральной функцией
|
| 0, x ≤ 0 | |
| 2 |
| ,0 < x ≤12 |
F(x)= x |
| 144 | |
|
|
| |
| 1, x >12 | ||
|
| ||
Используя неравенство Чебышева: оцените вероятность того, что |Х - М(х)|< 6 ;
2.В каких пределах находится случайная положительная величина X с вероятностью 0,8, если MX = 2?
3.Пользуясь неравенством Чебышева, оцените вероятность того, что из посеянных 5000 семян число взошедших окажется от 3750 до 4250, если известно, что М(Х) = 4000. Определите вероятность попадания случайной величины в заданный интервал.
4.Вероятность наступления события А в каждом из 1000 независимых опытов равна 0,8. Оцените вероятность того, что число наступлений события А в этих 1000 опытах отклонится от своего математического ожидания по модулю меньше чем на 50.
studfiles.net
Вариант 4.
1. Собрание, на котором присутствует 25 человек, в том числе 5 женщин, выбирает делегацию из трех человек. Считая, что каждый из присутствующих может быть избран с одинаковой вероятностью, найти вероятность того, что в делегацию войдут 2 женщины и 1 мужчина.
2. Бросают 2 игральные кости. Найти вероятность того, что на верхних гранях появятся одно четное и одно нечетное число очков.
3. Слово «АЛГОРИТМ» разрезано по буквам на карточки. Затем карточки перемешивают и вынимают без возвращения по одной. Найти вероятность того, что карточки в порядке появления образуют слово а) АЛГОРИТМ, б) ГОРА.
4. В урне содержится 7 черных и 4 белых шара. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них:
а) 2 белых шара;
б) менее двух белых шаров;
в) хотя бы 1 белый шар.
5. Вероятность появления события А в одном испытании равна 0,7. Вычислить вероятности следующих событий:
а) событие А наступит 3 раза в серии из 5 независимых испытаний;
б) событие А наступит ровно 2 раза в серии из 500 независимых испытаний.
в) событие А наступит не менее 160 и не более 180 раз в серии из 250
независимых испытаний.
6. В мастерской имеется 12 моторов. При определенном режиме работы вероятность того, что мотор в данный момент работает с полной нагрузкой, равна 0,8. Найти вероятность того, что в данный момент не менее 10 моторов работают с полной нагрузкой.
7. В первой урне 5 белых и 4 черных шара, а во второй – 7 белых и 4 черных шара. Из первой урны случайным образом вынимают 1 шар, а из второй – 4 шара. Найти вероятность того, что среди вынутых шаров только 3 белых шара.
8. Имеются 2 партии изделий. В первой партии 8 изделий, а во второй – 6 изделий. В каждой партии одно изделие бракованное. Изделие, взятое из первой партии, переложили во вторую партию, после чего взяли изделие из второй партии. Найти вероятность того, что изделие, выбранное из второй партии, бракованное.
9. В шар вписан правильный тетраэдр. В шаре наудачу зафиксирована точка. Какова вероятность того, что эта точка окажется в тетраэдре?
10. Дан закон распределения случайной величины X :
| X | 0 | 2 | 4 | 6 |
| p | 0,1 | 0,1 | 0,2 | 0,6 |
Найти функцию распределения
F (x ),значение
F (0).Вычислитьвероятностьтого,что
X приметзначениеиз интервала(0;4). Построитьмногоугольникраспределения.
11. ИзвестнафункцияраспределениядискретнойслучайнойвеличиныX :
⎧ 0,
⎪
x <0
F (x)=⎪0,4,0≤x <2
⎨
⎪0,5,2≤x <4
⎩⎪1,
x ≥4.
Задать закон распределения случайной величины X в виде таблицы.
12. Заданзаконраспределениядискретнойслучайнойвеличины:
| X | 140 | 160 | 180 | 200 | 220 |
| p | 0,1 | 0,15 | 0,25 | 0,35 | 0,15 |
Вычислить ее математическое ожидание, дисперсию и среднее квадратическое
отклонение.
13. Вероятность изготовления нестандартного изделия при налаженном технологическом процессе постоянна и равна 0,1. Для проверки качества выпускаемых изделий ОТК берет из партии не более 4-х изделий. При обнаружении нестандартного изделия вся партия задерживается. Написать закон распределения числа изделий, проверяемых ОТК в каждой партии. Найти математическое ожидание и дисперсию этой случайной величины.
14. Всхожесть семян кукурузы в некоторых условиях равна 90%. Найти границы для частоты взошедших семян из 900 посеянных, если эти границы надо гарантировать с вероятностью не меньшей 0,99.
15. На телефонной станции неправильное соединение происходит с вероятностью 0,002.
Найти вероятность того, что среди 1000 соединений произойдет:
а) ровно 2 неправильных соединения;
б) больше четырех неправильных соединений.
16. СлучайнаявеличинаX заданафункциейраспределения
⎧ 0,
⎪
x
p(x)=⎨ ,
⎪6
x <0
0≤x < 12
⎪⎩0, x ≥
12.
Найти функцию распределения
F (x )
случайной величины X . Построить графики
функций
p (x ) и
F (x ). Вычислить для этой случайной величины математическое
ожидание, дисперсию, среднее квадратическое отклонение, моду и медиану.
17. СлучайнаявеличинаХ заданафункциейраспределения
⎧0,
x <0
F (x)=⎪a ⋅arctgx,
⎨
⎪
0≤x <1
Найти а) параметр a ;
б) плотность распределения
⎩
p (x );
1, x ≥1.
в) вероятностьтого,чтоврезультатеодногоиспытанияслучайнаявеличина X
⎛
приметзначениеиз интервала⎜
⎜
⎝
3 ⎞
; 1⎟;
⎟
3 ⎠
г) математическое ожидание и дисперсию данной случайной величины;
д) вероятность того, что в результате 450 независимых испытаний случайная величина X примет 160 раз значение из указанного интервала.
18. Случайнаявеличина X распределенаравномернонаотрезке[1,3;5,3]. Найтивыражения
для плотности распределения и функции распределения этой случайной величины.
Вычислить математическое ожидание и дисперсию случайной величины X .
19. Случайная величина распределена по показательному закону с параметром 5,4. Записать выражения для плотности распределения и функции распределения этой случайной величины. Построить их графики. Вычислить математическое ожидание и дисперсию случайной величины X .
20. Случайная величина распределена по нормальному закону с параметрами
Найти вероятность того, что эта случайная величина примет значение
а) из промежутка [2; 26];
б) меньшее 8;
в) большее 15;
a =12
иσ=8.
г) отличающееся от своего среднего значения по абсолютной величине не более чем на 11.
21. Размер диаметра детали, выпускаемой предприятием, распределен по нормальному закону с математическим ожиданием 5см и дисперсией 0,81см. Найти вероятность того, что диаметр наудачу взятой детали отклонится от математического ожидания не более чем на
2см.
22. По выборке А решить следующие задачи:
а) составить вариационный ряд,
б) вычислить относительные и накопленные частоты,
в) построить эмпирическую функцию распределения и ее график,
г) вычислить числовые характеристики вариационного ряда: выборочную среднюю, дисперсию, среднее квадратическое отклонение, моду, медиану.
д) приуровне значимостиα= 0,05
проверить гипотезуо распределении Пуассона
соответствующей генеральной совокупности.
Выборка А:
| 0 | 0 | 2 | 0 | 1 | 3 |
| 0 | 1 | 0 | 1 | 2 | 1 |
| 3 | 0 | 0 | 2 | 1 | 3 |
| 2 | 2 | 1 | 3 | 3 | 2 |
| 0 | 2 | 4 | 3 | 2 | 1 |
| 3 | 3 | 1 | 1 | 1 | 3 |
| 2 | 1 | 0 | 1 | 2 | 1 |
| 2 | 2 | 2 | 2 | 5 | 5 |
| 2 | 3 | 2 | 5 | 0 | 3 |
| 2 | 1 | 4 | 3 | 5 | 2 |
23 По выборке В решить следующие задачи:
а) составить вариационный ряд, построить полигон и гистограмму;
б) вычислить относительные и накопленные частоты,
в) построить эмпирическую функцию распределения и ее график,
г) вычислить числовые характеристики вариационного ряда: выборочную среднюю, дисперсию, среднее квадратическое отклонение, моду, медиану.
д) при уровне значимости
α=0,05
проверить гипотезу о нормальном
распределении соответствующей генеральной совокупности.
Выборка В:
| –29 | –22 | –16 | –20 | –16 | –18 | –28 | –20 |
| –32 | –22 | –23 | –26 | –10 | –25 | –25 | –29 |
| –29 | –19 | –12 | –26 | –18 | –20 | –19 | –24 |
| –20 | –20 | –19 | –26 | –23 | –11 | –26 | –30 |
| –23 | –30 | –18 | –20 | –13 | –17 | –24 | –28 |
| –26 | –21 | –21 | –26 | –24 | –25 | –35 | –23 |
| –24 | –25 | –20 | –23 | –17 | –11 | –22 | –19 |
| –19 | –25 | –29 | –23 | –16 | –25 | –15 | –18 |
| –17 | –19 | –21 | –12 | –24 | –30 | –13 | –33 |
| –22 | –32 | –19 | –18 | –23 | –27 | –32 | –34 |
studfiles.net