Популяционная модель ограниченного роста. Модель ограниченного роста массы растений в excel
Изучение темы "Компьютерные модели"
Разделы: Биология, Информатика, Экология
1. Исходные положения или отправные точки.
“Если человеку каждый раз, столкнувшись с очередной жизненной задачей, приходилось бы с нуля решать ее, то едва ли прогресс человечества достиг бы сегодняшних высот. Разумеется, каждый человек и общество в целом опирается на опыт предшествующих поколений”.
Эта цитата из учебника “Информатика 10–11” авторов А. Г. Гейн, А. И. Сенокосов, Н. А. Юнерман является главной отправной точкой представляемой здесь работы.
Моя цель – рассказать о том, как выстраивается единая линия в изучении темы “Компьютерные модели” в 6 классе МБОУ – Лицей № 4 г. Краснодар.
На тему отводится 8 часов в течение третьей учебной четверти. Заметим, что в первой четверти учащиеся знакомятся с электронными таблицами. Во второй четверти изучается теоретический материал по теме “ Моделирование”. Учащиеся понимают значения терминов, знают этапы решения задачи с применением компьютера. Знакомы с понятием “адекватность модели”.
В процессе изучения темы “Компьютерные модели” ученики выполняют практические работы в среде электронных таблиц, логическим завершением которых являются задача о разумном подходе к потреблению природных ресурсов. Решая задачу “Прирост массы растений”, дети постепенно уточняют и совершенствуют модели, последовательно применяя “Модель неограниченного роста”, “Модель ограниченного роста”, “Модель потребления возобновляемых ресурсов”. Причем переход к модели другого вида логически обоснован.
В результате завершения работ по всему циклу и опираясь на результаты компьютерного моделирования, дети с большим удовольствием отвечают на вопрос: “Сколько можно брать у живой природы, чтобы ее запасы не истощались?”, что само по себе имеет большое воспитательное значение, акцентирует внимание на бережном отношении к окружающей среде и находит отклик в душах детей среднего школьного возраста.
2. Рост числа фазанов. Модель неограниченного роста.
Сформулируем задачу. В 1937 г. на остров Протекшн завезли 8 фазанов. Никто на этих фазанов не охотился (ни люди, ни звери), корма и воды было вдоволь, и через год фазанов стало 26, а еще через год их было 83. Сколько будет фазанов через заданное число лет?
I. Постановка задачи.
Для решения нашей задачи мы намерены использовать компьютер, значит, надо строить компьютерную модель. Выделим существенные факторы.
Окружающая среда выступает как регулятор прироста количества фазанов. Факторов, влияющих на жизнь фазанов много и все их учесть в принципе невозможно. Поэтому условимся рассматривать воздействие окружающей среды на численность популяции фазанов как черный ящик
Черный ящик имеет один вход – численность фазанов на начало года и один выход – число фазанов по прошествии года. Естественно также предположить, что прирост числа фазанов через год пропорционален уже имеющемуся количеству особей, что вполне согласуется с обычными представлениями о размножении.
Таким образом, мы выделяем два существенных фактора:
Начальное количество – М0 и коэффициент прироста за 1 год – К.
II. Создание математической модели.
Число фазанов по истечению n лет обозначим Mn , тогда прирост за один год составит Mn+1 – Mn или К* Mn
Установим связь между параметрами модели: Mn+1 = Mn *(К+1)
Построенную модель называют моделью неограниченного роста.
Сформулируем выводы. Мы построили модель неограниченного роста. Легко заметить, что численность особей растет в геометрической прогрессии, с учетом исходного предположения о том, что действие окружающей среды сказывается только на скорости прироста фазанов. Нетрудно предположить, что применить эту модель можно и для любых других живых организмов. (Смотри Приложение 1, Приложение 2)
3. Прирост массы растений Модель неограниченного роста.
Решая предыдущую задачу, мы построили модель неограниченного роста – модель некоторого природного процесса, пригодную для любых живых организмов, участвующих в этом процессе. Применим эту модель для решения другой задачи. “Прирост массы растений”.
Сформулируем задачу. Используя модель неограниченного роста, проследить за изменением массы растений двух климатических зонах: тундре и тайге.
I. Постановка задачи.
Очевидно, что масса растений на различных территориях будет увеличиваться с разной скоростью. Будем использовать значения коэффициента размножения, экспериментально полученные учеными – биологами для растений в различных природных зонах.
Пусть первоначальная масса растений на некотором участке в каждой из климатических зон равнялась 1 тонне. Напомним два существенных фактора для решения нашей задачи: Начальная масса растений – М0 и коэффициент прироста за 1 год – К
II. Математическая модель.
Будем использовать уже знакомую нам модель неограниченного роста Mn+1 =Mn *(К+1)
IV. Компьютерный эксперимент.
Подготовим таблицу для записи результатов четырех опытов.
| Опыт | Природная зона | Тундра | Тайга | |||
| Коэффициент прироста | 0,6 | 1,8 | ||||
| Начальная масса растений (т) | 1 | 1 | ||||
| 1 | Опыт 1: Через сколько лет масса растений превысит 100 т? | 10 лет | 5 лет | |||
| 2 | Опыт 2: Через сколько лет масса растений превысит 1000 т? | 15 лет | 7 лет | |||
| 3 | Опыт 3: Через сколько лет масса растений превысит 10 000 т? | 20 лет | 9 лет | |||
| 4 | Опыт 4: Через сколько лет масса растений превысит массу Земли 5 976 000 000 000 000 000 000 т? | 107 лет | 49 лет | |||
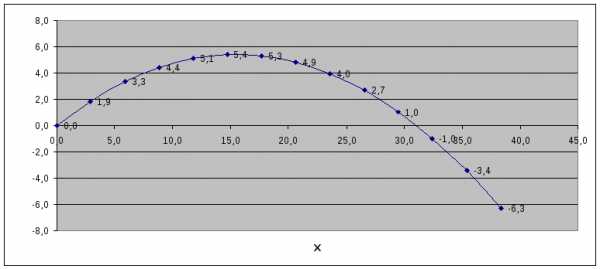
Построим диаграммы для наглядного представления процесса роста растений в тундре для опытов 1, 2 и 3. (Смотри Приложение 3, Приложение 4)
Сформулируем выводы. В течение жизни одного поколения вся планета превратится в “зеленое море” растений! Есть над чем призадуматься... Видно не все удачно в построенной нами модели. Напомним, что первоначально мы условились о том, что окружающая среда оказывает влияние только на скорость прироста числа особей или массы растений.
Принцип адекватности модели говорит еще и о том, что никакая модель не эквивалентна реальному объекту (процессу или явлению). Проблема адекватности – одна из самых трудных.
Модель неограниченного роста хорошо согласуется с практикой, пока масса живых организмов остается достаточно малой.
В некоторых случаях, когда коэффициент прироста невелик и мала начальная масса, это условие может выполняться годами, так, что экспериментально опровергнуть такую модель бывает довольно трудно. Но в нашем случае налицо нарушение фундаментального закона природы – закона сохранения массы. Продолжим работу над совершенствованием модели.
4. Прирост массы растений. Модель ограниченного роста.
Почему же, однажды родившись, модели не живут вечно? Некоторые из них исчезают, едва появившись на свет. Другие живут столетиями. Но даже модели, построенные лучшими умами человечества, вся равно сменяются другими. Что управляет этой сложной жизнью моделей?
Прежде всего: растут знания человека об окружающем мире, вот и меняются модели. И второе: смена модели может происходить и в силу того, что она не согласуется с более общими законами, открытыми человеком при исследовании природы и общества.
Именно так и случилось, когда мы исследовали рост растений, опираясь на модель неограниченного роста. Выявилось нарушение фундаментального закона природы – закона сохранения массы. Быстрый рост массы растений можно было заранее предвидеть, исходя из математических свойств геометрической прогрессии. Модель оставалась адекватной только при малой начальной массе и малой величине коэффициента прироста.
Продолжим уточнение модели. Конечно, ни при каких, даже самых благоприятных, условиях масса растений не может превысить массу планеты. Выдвинем предположение, что имеется некоторое предельное значение массы растений, “проживающих” на той или иной территории. Так, ученые показали, что запас массы растений не может превосходить 20 т на гектар в полярной зоне и 350 т на гектар в лесной зоне. Это означает, что рост растений ограничен.
И еще одно предположение: чем ближе масса растений к предельно допустимой, тем меньшим становится коэффициент прироста К, т.к. Сначала растения быстро набирают массу, а затем их рост замедляется. Совершенствуя модель, ученые – биологи предложили использовать новую величину – коэффициент пропорциональности А.
Сформулируем задачу. Используя модель ограниченного роста, проследить за изменением массы растений двух климатических зонах: тундре и тайге.
I. Постановка задачи.
Существенные факторы:
Начальная масса растений – М0
Коэффициент прироста за 1 год – Кn
Предельное значение массы живых организмов – L
Коэффициент пропорциональности – А
II. Математическая модель.
Зададим связи между параметрами модели:
Коэффициент прироста будет меняться по формуле Кn=А*(L – Mn ),
где коэффициент пропорциональности находится из соотношения А= К/(L – M0).
Поэтому формула примет вид Mn+1 =Mn + Mn *А*(L – Mn )
Эту модель принято называть моделью ограниченного роста.
IV. Компьютерный эксперимент.
Подготовим таблицу для записи результатов трех компьютерных экспериментов. Сравним новые результаты, полученные при испытании модели ограниченного роста с результатами аналогичных опытов, полученных при работе с моделью неограниченного роста Проанализируем результаты и сделаем выводы.
| № | Природная зона | Неограниченный рост | Ограниченный рост | ||
| Тундра | Тайга | Тундра | Тайга | ||
| 1 | Опыт 1: Через сколько лет масса растений превысит 100 т? | 10 лет | 5 лет | 10 лет | 5 лет |
| 2 | Опыт 2: Через сколько лет масса растений превысит 1 000 т? | 15 лет | 7 лет | 15 лет | 7 лет |
| 3 | Опыт 3: Через сколько лет масса растений превысит 10 000 т? | 20 лет | 9 лет | 23 года | 10 лет |
Построим диаграммы для наглядного представления процесса роста растений в тундре для опытов 1, 2 и 3. Сравним с ранее построенными диаграммами. (Смотри Приложение 5, Приложение 6).
Сформулируем выводы. Так как для решения задачи применяется модель ограниченного роста, то наблюдается ежегодное уменьшение коэффициента прироста, что не может не сказаться на величине массы растений. Результаты первых двух опытов при относительно малых массах растений совпадают. Результаты третьего эксперимента говорят о том, что наряду с увеличением массы растений стало наблюдаться замедление их роста.
5. Сколько можно брать у природы? Модель потребления возобновляемых ресурсов. Управление процессами.
Человек, познавая природу и общество, все активнее и шире вмешивается в действие факторов, влияющих на функционирование этих систем. Влияние это, чаще сознательное, преследует цель – заставить систему функционировать нужным человеку образом, то есть управлять системой. Компьютерное моделирование может применяться и для решения задач управления.
Рассмотрим проблему добычи леса. Лес относится к так называемым возобновляемым ресурсам. Возникает задача управления: сколько леса можно рубить ежегодно, чтобы обеспечить его нормальное воспроизводство?
За основу для решения задачи возьмем уже знакомую нам модель ограниченного роста. Отметим, что появился еще один существенный фактор – воздействие человека. Будем считать, что объем вырубаемого леса в течение года не меняется, поэтому формула изменится незначительно:
Mn+1 =Mn + Mn *А*(L – Mn ) – R,
где R – это объем вырубки.
Такую модель называют моделью потребления возобновляемых ресурсов.
Сформулируем задачу. Используя модель потребления возобновляемых ресурсов, найти оптимальный объем вырубки, при котором будет обеспечено его нормальное воспроизводство.
I. Постановка задачи.
Решать задачу будем только для одной климатической зоны – тайги.
Существенных факторы:
Начальная масса растений – М0
Коэффициент прироста за 1 год – Кn
Предельное значение массы живых организмов – L
Коэффициент пропорциональности – А
Объем вырубки – R
II. Математическая модель.
Удобно рассмотреть еще одну величину: ежегодный прирост – Р
Зададим связи между параметрами модели:
Mn+1 =Mn + Mn *А*(L – Mn ) – R,
Коэффициент прироста будет меняться по формуле Кn=А*(L – Mn ),
где коэффициент пропорциональности находится из соотношения
А= К/(L – M0)
Ежегодный прирост рассчитывается по формуле Р= Mn *А*(L – Mn )
IV. Компьютерный эксперимент.
| Опыт | Природная зона | Тайга |
| 1 | Опыт 1: Объем ежегодной вырубки древесины 1 000 т | Через определенный промежуток времени наступает равновесие: величина прироста в точности совпадает с забираемой массой и равна 1 000 т. Масса древесины равна 10 413 т, что превышает начальный уровень 10 000 т |
| 2 | Опыт 2: Объем ежегодной
вырубки древесины 3 000 т
|
Через несколько лет наступает равновесие: величина прироста в точности совпадает с забираемой массой и равна 3 000 т. Масса древесины равна 8 952 т, что меньше начального уровня 10 000 т |
| 3 | Опыт 3: Объем ежегодной вырубки древесины 5 000 т | Равновесие в природе не наступает. Уровень прироста меньше объема вырубки древесины. Через 30 лет лес погибнет. |
| 4 | Опыт 4: Найти оптимальный объем ежегодной вырубки леса, при котором будет сохраняться его нормальное воспроизводство | Оптимальный объем
составляет 1637 т ежегодно. При этом в природе
наступает равновесие. Масса древесины равна начальной массе 10 000 т. |
Построим диаграммы. (Смотри Приложение 7, Приложение 8).
Мы нашли ответ на вопрос: “Сколько можно брать у живой природы, чтобы ее запасы не истощались?” Для того чтобы, ресурсы возобновлялись, можно производить вырубку леса в объемах, не превышающих 1 637 т ежегодно при начальной массе 10 000 т.
(См. Презентацию)
3.04.2013
xn--i1abbnckbmcl9fb.xn--p1ai
Популяционная модель ограниченного роста
Documents войти Загрузить ×- No category
Related documents

Задания части С.

Тестовые задания по дисциплине «Экология» (необходимо выбрать один правильный ответ)
Популяционная и эволюционная генетика

Экология - Мозырский государственный педагогический

Модель эволюции популяции высокотехнологичных фирм

ВОПРОСЫ К ЗАЧЕТУ.

Контрольная работа № 2 по "Экологии". Задание №1 Исходя из
Тема: Структуры популяции

Календарно тематический план лаб. занятий и семинаров 2015-16

ДОКЛАД Взгляд в будущее планеты
Скачать advertisement StudyDoc © 2018 DMCA / GDPR Пожаловатьсяstudydoc.ru
Создание компьютерной модели: «Биологические модели развития популяции»
Тема: Создание компьютерной модели
«Биологические модели развития популяции»
Тип урока: самостоятельная лабораторная работа
Цели:
Сформировать у учащихся понятия моделирования как метода познания и «компьютерная информационная модель»;
Познакомить детей с основными этапами моделирования;
Сформировать понимание обязательного соблюдения этапов моделирования;
Определение уровня практических навыков создания компьютерных моделей в среде MS Excel;
Формирование общих представлений современной научной картины мира;
Формирование коммуникативных качеств развивающейся личности.
Оборудование:
ПК;
Интерактивная доска;
MS PowerPoint
MS Excel
Ход урока:
I.Организационный момент (5 мин.)
Приветствие. Сообщение новой темы.
Проведение краткого инструктажа перед работой за компьютером
II. Актуализация знаний (5 мин.)
Проверка домашнего задания - стр. 69 №7
III. Самостоятельная работа (30 мин.)
На экране демонстрируется пример выполненной лабораторной работы
Лабораторная работа №3
Самостоятельная работа
Задача. Биологические модели развития популяции. Модель типа «хищник – жертва».
Описание задачи.
В модели «хищник – жертва» количество жертв Xn и количество хищников yn связаны между собой.Xn+1=(a-b*xn)*xn-c-f*xn*yn, где f- возможность гибели жертвы при встрече с хищниками.Yn+1=d*yn+e*xn*yn, где d- скорость уменьшения популяции хищников, е- характеризует величину роста численности хищников за счет жертв.
Компьютерная модель
В ячейки В1 и В6 внести начальные значения численности популяций жертв и хищников.В ячейки В2:В5 внести значения коэффициентов a,b,c,f, влияющие на изменение численности жертв. В ячейки В7 и В8 внести значения коэффициентов d,e, влияющих на изменение численности хищников.В столбце D будем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбце Е – ограниченного роста, в столбце F- ограниченного роста с отловом, в столбцах G,H- «хищник – жертва».
В ячейки D1,E1,F1,G1 внести значения начальной численности популяций жертв, в ячейку Н1-хищников. В ячейку D2 внести рекуррентную формулу ограниченного роста =$B$2*D1В ячейку E2 внести рекуррентную формулу ограниченного роста =($B$2-$B$3*E1)*E1В ячейку F2 внести рекуррентную формулу ограниченного роста с отловом =($B$2-$B$3*F1)*F1-$B$4В ячейку G2 внести рекуррентную формулу изменения количества жертв =($B$2-$B$3*G1)*G1-$B$4-$B$5*G1*h2В ячейку Н2 внести рекуррентную формулу изменения количества хищников =$B$7*h2+$B$8*G1*h2
Скопировать внесенные формулы в ячейки столбцов.Ознакомиться с динамикой изменения численности популяций.Построить график изменения популяций с течением времени (построить диаграмму типа График).Изменяя значения начальных численностей популяций, а также коэффициенты, получить различные варианты изменения численности популяций в зависимости от времени.
Начальные данные
IV. Итог урока (2 мин.)
V. Домашнее задание (3 мин.) §13, повторить
xn--j1ahfl.xn--p1ai
Изучение темы Компьютерные модели |
1. Исходные положения или отправные точки.
“
Если человеку каждый раз, столкнувшись с очередной жизненной задачей,приходилось бы с нуля решать ее, то едва ли прогресс человечества достиг бысегодняшних высот. Разумеется, каждый человек и общество в целом опирается наопыт предшествующих поколений”.
Эта цитата из учебника “Информатика 10–11” авторов А. Г. Гейн, А. И.Сенокосов, Н. А. Юнерман является главной отправной точкой представляемой здесьработы.
Моя цель – рассказать о том, как выстраивается единая линия в изучении темы“Компьютерные модели” в 6 классе МБОУ – Лицей № 4 г. Краснодар.
На тему отводится 8 часов в течение третьей учебной четверти. Заметим, что впервой четверти учащиеся знакомятся с электронными таблицами. Во второй четвертиизучается теоретический материал по теме “ Моделирование”. Учащиеся понимаютзначения терминов, знают этапы решения задачи с применением компьютера. Знакомыс понятием “адекватность модели”.
В процессе изучения темы “Компьютерные модели” ученики выполняют практическиеработы в среде электронных таблиц, логическим завершением которых являются задача о разумном подходе к потреблению природных ресурсов. Решая задачу“Прирост массы растений”, дети постепенно уточняют и совершенствуют модели,последовательно применяя “Модель неограниченного роста”, “Модель ограниченногороста”, “Модель потребления возобновляемых ресурсов”. Причем переход к моделидругого вида логически обоснован.
В результате завершения работ по всему циклу и опираясь на результатыкомпьютерного моделирования, дети с большим удовольствием отвечают на вопрос: “Сколько можно брать у живой природы, чтобы ее запасы не истощались?”, чтосамо по себе имеет большое воспитательное значение, акцентирует внимание на бережном отношении к окружающей среде и находит отклик в душах детейсреднего школьного возраста.
2. Рост числа фазанов. Модель неограниченного роста.
Сформулируем задачу.
В 1937 г. на остров Протекшн завезли 8 фазанов.Никто на этих фазанов не охотился (ни люди, ни звери), корма и воды быловдоволь, и через год фазанов стало 26, а еще через год их было 83. Сколько будетфазанов через заданное число лет?
I. Постановка задачи.
Для решения нашей задачи мы намерены использовать компьютер, значит, надостроить компьютерную модель. Выделим существенные факторы.
Окружающая среда выступает как регулятор прироста количества фазанов.Факторов, влияющих на жизнь фазанов много и все их учесть в принципе невозможно.Поэтому условимся рассматривать воздействие окружающей среды на численностьпопуляции фазанов как черный ящик
Черный ящик имеет один вход – численность фазанов на начало года и один выход– число фазанов по прошествии года. Естественно также предположить, что приростчисла фазанов через год пропорционален уже имеющемуся количеству особей, чтовполне согласуется с обычными представлениями о размножении.
Таким образом, мы выделяем два существенных фактора:
Начальное количество – М0 и коэффициент прироста за 1 год – К.
II. Создание математической модели.
Число фазанов по истечению n лет обозначим Mn , тогда прирост за один годсоставит Mn+1 – Mn или К* Mn
Установим связь между параметрами модели: Mn+1 = Mn *(К+1)
Построенную модель называют моделью неограниченного роста.
Сформулируем выводы. Мы построили модель неограниченного роста.Легко заметить, что численность особей растет в геометрической прогрессии, сучетом исходного предположения о том, что действие окружающей среды сказываетсятолько на скорости прироста фазанов. Нетрудно предположить, что применитьэту модель можно и для любых других живых организмов. (Смотри Приложение 1, Приложение 2)
3. Прирост массы растений Модель неограниченного роста.
Решая предыдущую задачу, мы построили модель неограниченного роста – модельнекоторого природного процесса, пригодную для любых живых организмов,участвующих в этом процессе. Применим эту модель для решения другой задачи.“Прирост массы растений”.
Сформулируем задачу.
Используя модель неограниченного роста,проследить за изменением массы растений двух климатических зонах: тундре итайге.
I. Постановка задачи.
Очевидно, что масса растений на различных территориях будет увеличиваться сразной скоростью. Будем использовать значения коэффициента размножения,экспериментально полученные учеными – биологами для растений в различныхприродных зонах.
Пусть первоначальная масса растений на некотором участке в каждой изклиматических зон равнялась 1 тонне. Напомним два существенных фактора длярешения нашей задачи: Начальная масса растений – М0 и коэффициент приростаза 1 год – К
II. Математическая модель.
Будем использовать уже знакомую нам модель неограниченного роста Mn+1=Mn *(К+1)
IV. Компьютерный эксперимент.
Подготовим таблицу для записи результатов четырех опытов.
| Опыт | Природнаязона | Тундра | Тайга | |||
| Коэффициентприроста | 0,6 | 1,8 | ||||
| Начальнаямасса растений (т) | 1 | 1 | ||||
| 1 | Опыт 1: Черезсколько лет масса растений превысит 100 т? | 10 лет | 5 лет | |||
| 2 | Опыт 2: Черезсколько лет масса растений превысит 1000 т? | 15 лет | 7 лет | |||
| 3 | Опыт 3: Черезсколько лет масса растений превысит 10 000 т? | 20 лет | 9 лет | |||
| 4 | Опыт 4: Черезсколько лет масса растений превысит массу Земли 5 976 000 000 000 000000 000 т? | 107 лет | 49 лет | |||
Построим диаграммы для наглядного представления процесса ростарастений в тундре для опытов 1, 2 и 3. (Смотри Приложение 3,Приложение 4)
Сформулируем выводы.
В течение жизни одного поколения вся планетапревратится в “зеленое море” растений! Есть над чем призадуматься… Видно невсе удачно в построенной нами модели. Напомним, что первоначально мы условилисьо том, что окружающая среда оказывает влияние только на скорость прироста числаособей или массы растений.
Принцип адекватности модели говорит еще и о том, что никакая модель неэквивалентна реальному объекту (процессу или явлению). Проблема адекватности –одна из самых трудных.
Модель неограниченного роста хорошо согласуется с практикой, пока масса живыхорганизмов остается достаточно малой.
В некоторых случаях, когда коэффициент прироста невелик и мала начальнаямасса, это условие может выполняться годами, так, что экспериментальноопровергнуть такую модель бывает довольно трудно. Но в нашем случае налицонарушение фундаментального закона природы – закона сохранения массы. Продолжимработу над совершенствованием модели.
4. Прирост массы растений. Модель ограниченного роста.
Почему же, однажды родившись, модели не живут вечно? Некоторые из нихисчезают, едва появившись на свет. Другие живут столетиями. Но даже модели,построенные лучшими умами человечества, вся равно сменяются другими. Чтоуправляет этой сложной жизнью моделей?
Прежде всего: растут знания человека об окружающем мире, вот именяются модели. И второе: смена модели может происходить и в силу того, что онане согласуется с более общими законами, открытыми человеком приисследовании природы и общества.
Именно так и случилось, когда мы исследовали рост растений, опираясь намодель неограниченного роста. Выявилось нарушение фундаментального законаприроды – закона сохранения массы. Быстрый рост массы растений можно былозаранее предвидеть, исходя из математических свойств геометрической прогрессии.Модель оставалась адекватной только при малой начальной массе и малой величинекоэффициента прироста.
Продолжим уточнение модели. Конечно, ни при каких, даже самых благоприятных,условиях масса растений не может превысить массу планеты. Выдвинемпредположение, что имеется некоторое предельное значение массы растений,“проживающих” на той или иной территории. Так, ученые показали, что запас массырастений не может превосходить 20 т на гектар в полярной зоне и 350 т на гектарв лесной зоне. Это означает, что рост растений ограничен.
И еще одно предположение: чем ближе масса растений к предельно допустимой,тем меньшим становится коэффициент прироста К, т.к. Сначала растениябыстро набирают массу, а затем их рост замедляется. Совершенствуя модель, ученые– биологи предложили использовать новую величину – коэффициентпропорциональности А.
Сформулируем задачу. Используя модель ограниченного роста,проследить за изменением массы растений двух климатических зонах: тундре и тайге.
I. Постановка задачи.
Существенные факторы:
Начальная масса растений – М0
Коэффициент прироста за 1 год – Кn
Предельное значение массы живых организмов – L
Коэффициент пропорциональности – А
II. Математическая модель.
Зададим связи между параметрами модели:
Коэффициент прироста будет меняться по формуле Кn=А*(L – Mn),
где коэффициент пропорциональности находится из соотношения А= К/(L – M0).
Поэтому формула примет вид Mn+1 =Mn + Mn*А*(L – Mn )
Эту модель принято называть моделью ограниченного роста.
IV. Компьютерный эксперимент.
Подготовим таблицу для записи результатов трех компьютерных экспериментов.Сравним новые результаты, полученные при испытании модели ограниченного ростас результатами аналогичных опытов, полученных при работе с модельюнеограниченного роста Проанализируем результаты и сделаем выводы.
| № | Природнаязона | Неограниченный рост | Ограниченный рост | ||
| Тундра | Тайга | Тундра | Тайга | ||
| 1 | Опыт 1: Через скольколет масса растений превысит 100 т? | 10 лет | 5 лет | 10 лет | 5 лет |
| 2 | Опыт 2: Через скольколет масса растений превысит 1 000 т? | 15 лет | 7 лет | 15 лет | 7 лет |
| 3 | Опыт 3: Через скольколет масса растений превысит 10 000 т? | 20 лет | 9 лет | 23 года | 10 лет |
Построим диаграммы для наглядного представления процесса ростарастений в тундре для опытов 1, 2 и 3. Сравним с ранее построенными диаграммами.(Смотри Приложение 5, Приложение 6).
Сформулируем выводы.
Так как для решения задачи применяется модельограниченного роста, то наблюдается ежегодное уменьшение коэффициентаприроста, что не может не сказаться на величине массы растений. Результаты первых двух опытов при относительно малых массах растений совпадают. Результаты третьего эксперимента говорят о том, что наряду с увеличением массы растений стало наблюдаться замедление их роста.
5. Сколько можно брать у природы? Модель потребления возобновляемых ресурсов.Управление процессами.
Человек, познавая природу и общество, все активнее и шире вмешивается вдействие факторов, влияющих на функционирование этих систем. Влияние это, чащесознательное, преследует цель – заставить систему функционировать нужнымчеловеку образом, то есть управлять системой. Компьютерное моделированиеможет применяться и для решения задач управления.
Рассмотрим проблему добычи леса. Лес относится к так называемым возобновляемым ресурсам. Возникает задача управления: сколько лесаможно рубить ежегодно, чтобы обеспечить его нормальное воспроизводство?
За основу для решения задачи возьмем уже знакомую нам модель ограниченногороста. Отметим, что появился еще один существенный фактор – воздействиечеловека. Будем считать, что объем вырубаемого леса в течение года не меняется,поэтому формула изменится незначительно:
Mn+1 =Mn + Mn *А*(L – Mn) – R,
где R – это объем вырубки.
Такую модель называют моделью потребления возобновляемых ресурсов.
Сформулируем задачу. Используя модель потребления возобновляемыхресурсов, найти оптимальный объем вырубки, при котором будет обеспечено егонормальное воспроизводство.
I. Постановка задачи.
Решать задачу будем только для одной климатической зоны – тайги.
Существенных факторы:
Начальная масса растений – М0
Коэффициент прироста за 1 год – Кn
Предельное значение массы живых организмов – L
Коэффициент пропорциональности – А
Объем вырубки – R
II. Математическая модель.
Удобно рассмотреть еще одну величину: ежегодный прирост – Р
Зададим связи между параметрами модели:
Mn+1 =Mn + Mn *А*(L – Mn) – R,
Коэффициент прироста будет меняться по формуле Кn=А*(L – Mn),
где коэффициент пропорциональности находится из соотношения
А= К/(L – M0)
Ежегодный прирост рассчитывается по формуле Р= Mn *А*(L – Mn)
IV. Компьютерный эксперимент.
| Опыт | Природная зона | Тайга |
| 1 | Опыт 1: Объем ежегоднойвырубки древесины 1 000 т | Через определенныйпромежуток времени наступает равновесие: величина прироста в точностисовпадает с забираемой массой и равна 1 000 т. Масса древесины равна 10413 т, что превышает начальный уровень 10 000 т |
| 2 | Опыт 2: Объем ежегоднойвырубки древесины 3 000 т | Через несколько летнаступает равновесие: величина прироста в точности совпадает сзабираемой массой и равна 3 000 т. Масса древесины равна 8 952 т, чтоменьше начального уровня 10 000 т |
| 3 | Опыт 3: Объем ежегоднойвырубки древесины 5 000 т | Равновесие в природе ненаступает. Уровень прироста меньше объема вырубки древесины.Через 30 лет лес погибнет. |
| 4 | Опыт 4: Найти оптимальныйобъем ежегодной вырубки леса, при котором будет сохраняться егонормальное воспроизводство | Оптимальный объемсоставляет 1637 т ежегодно. При этом в природе наступает равновесие. Масса древесины равна начальной массе 10 000 т. |
Построим диаграммы. (Смотри Приложение 7,Приложение 8).
Мы нашли ответ на вопрос: “Сколько можно брать у живой природы, чтобы еезапасы не истощались?” Для того чтобы, ресурсы возобновлялись, можнопроизводить вырубку леса в объемах, не превышающих 1 637 т ежегодно приначальной массе 10 000 т.
(См. Презентацию)
Внимание, только СЕГОДНЯ!goxi.ru
Министерство образования и науки рф
________________________________________________________________________________________
Государственное образовательное учреждение высшего профессионального образования
«Санкт-Петербургская государственная лесотехническая академия имени С.М.Кирова»
Кафедра математических методов и моделирования в экономике и управлении
Лабораторная работа№2
По дисциплине : «Математическое моделирование лесных экосистем».
Выполнила: студентка
ЛХФ 5курса 1 маг
Зачетная книжка№507043
Болдышевич А.А
Проверил: доктор технических наук, профессор
Гуров С.В
Санкт-Петербург
2012год
Лабораторная работа 2
МОДЕЛИ СВОБОДНОГО И ОГРАНИЧЕННОГО РОСТА ПОПУЛЯЦИЙ
1. Постановка задачи
В начальный момент времени 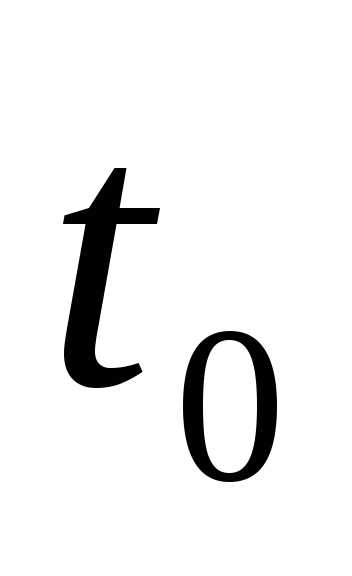 количественный состав некоторого биологического вида равен
количественный состав некоторого биологического вида равен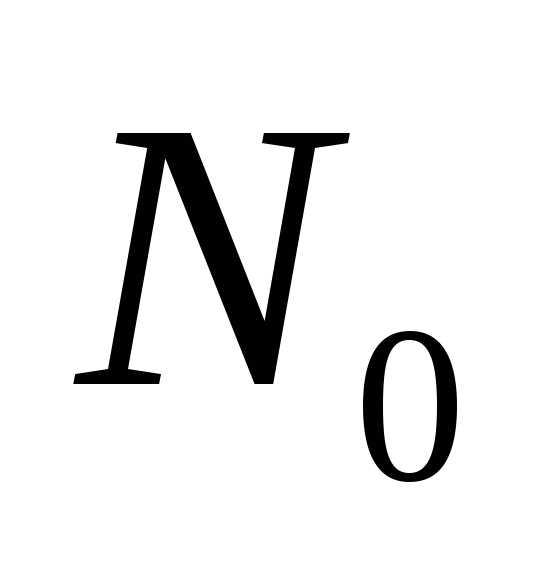 единиц. Требуется сделать прогноз численности
единиц. Требуется сделать прогноз численности 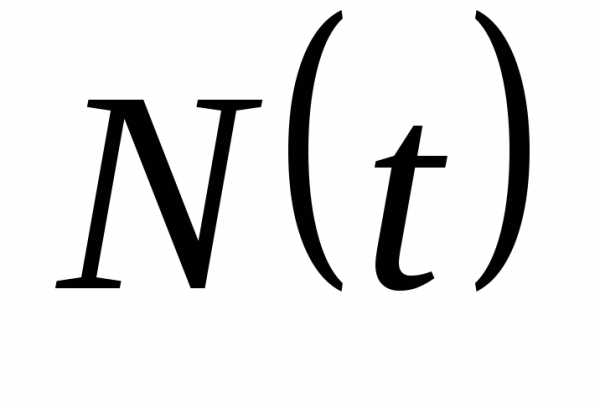 данной популяции при
данной популяции при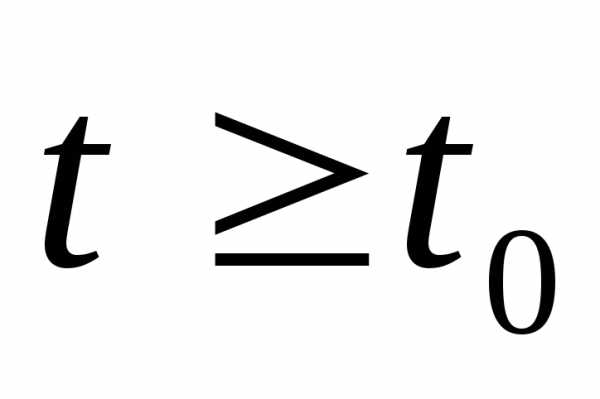 для двух случаев:
для двух случаев:
относительный темп прироста популяции не зависит от ее численности и равен постоянной величине
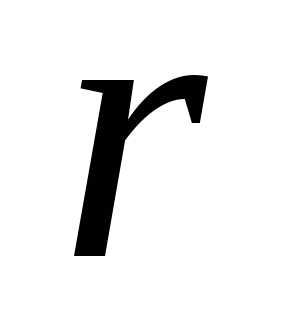 (свободный рост популяции),
(свободный рост популяции),относительный темп прироста популяции уменьшается линейно с увеличением ее численности и равен величине
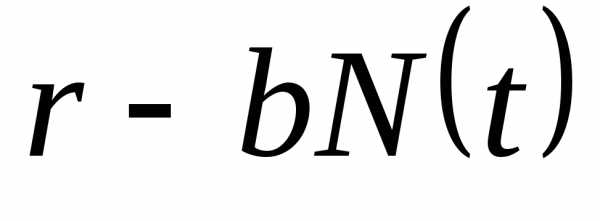 (ограниченный рост популяции).
(ограниченный рост популяции).
С этой целью необходимо
составить математическую модель свободного роста популяции в виде линейного дифференциального уравнения, найти аналитическое решение уравнения;
составить математическую модель ограниченного роста популяции в виде дифференциального уравнения Бернулли, определить аналитическое и численное решение уравнения при заданных начальных условиях, показать графически приближенное совпадение полученных решений;
привести графическую иллюстрацию изменения численности для моделей свободного и ограниченного роста популяции;
сделать выводы по работе.
2. Сведения из теории
2.1. Модель Мальтуса
В огромном числе случаев при попытке построить модель какого либо объекта либо невозможно прямо указать физические законы, которым он подчиняется, либо с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями. Что, казалось бы общего между радиоактивным распадом и динамикой популяций, в частности изменением численности населения нашей планеты? Однако на простейшем уровне такая аналогия вполне просматривается, о чем свидетельствует одна из простейших моделей популяций, называемая моделью Мальтуса. В ее основу положено простое утверждение — скорость изменения населения со временем 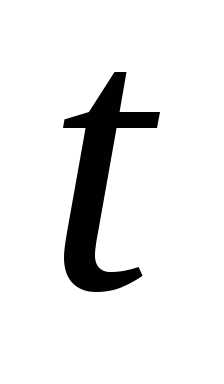 пропорциональна его текущей численности
пропорциональна его текущей численности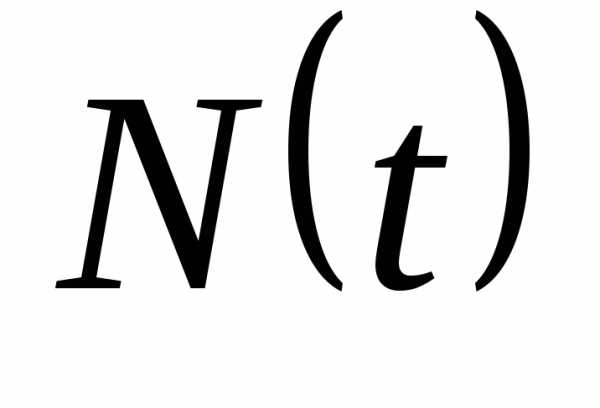 , умноженной на сумму коэффициентов рождаемости
, умноженной на сумму коэффициентов рождаемости 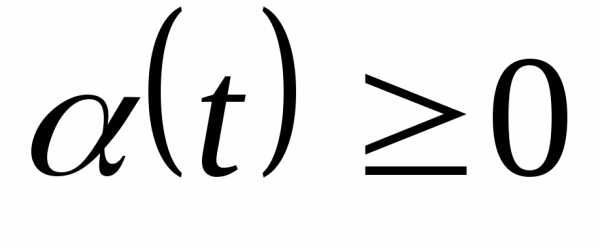 и смертности
и смертности 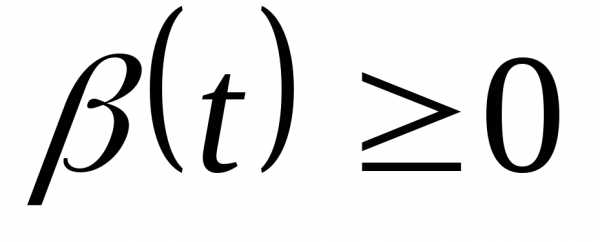 . В результате приходим к уравнению
. В результате приходим к уравнению
, (1)
которое похоже на уравнение радиоактивного распада и совпадающего с ним при 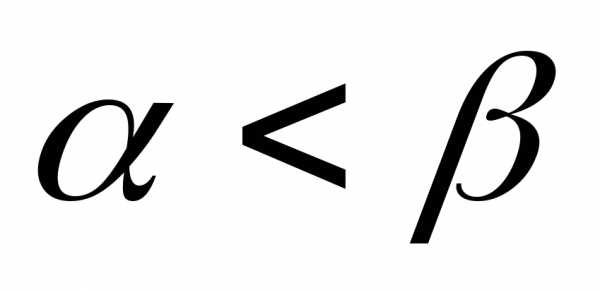 (если
(если и
и – постоянные). Это не удивительно, так как при их выводе использовались одинаковые соображения. Интегрирование выше приведенного уравнения дает
– постоянные). Это не удивительно, так как при их выводе использовались одинаковые соображения. Интегрирование выше приведенного уравнения дает
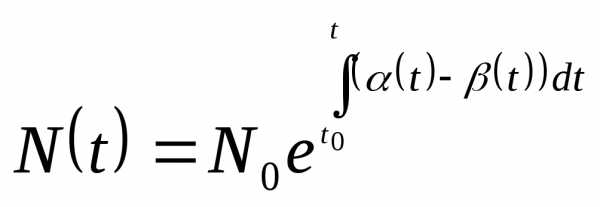 , при
, при 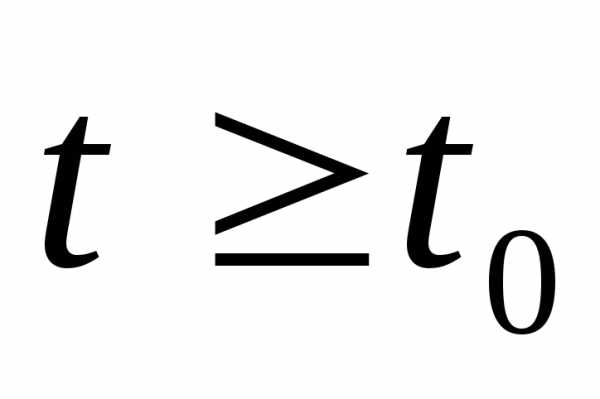 ,
,
где – численность населения в момент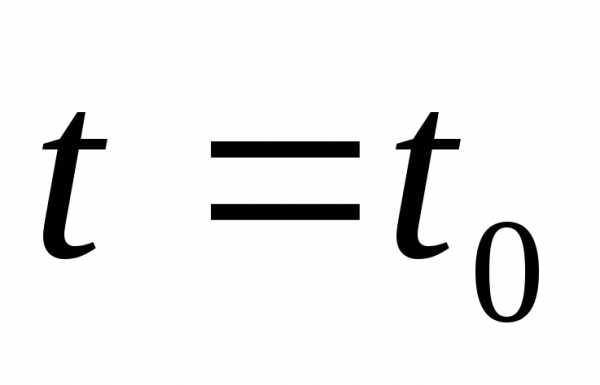 (начальная численность).
(начальная численность).
На рис. 1 приведены графики функции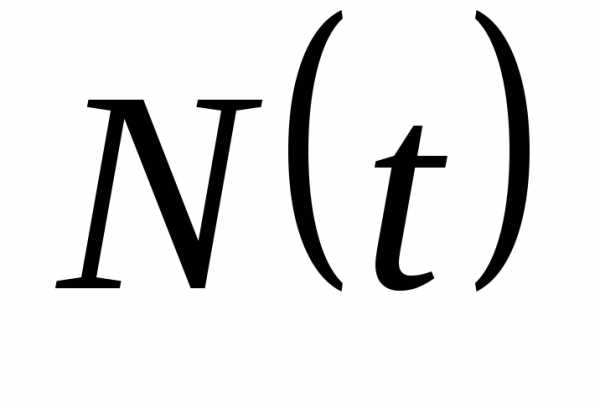 при постоянных
при постоянных  и
и (разным подобным друг другу кривыми соответствуют разные
(разным подобным друг другу кривыми соответствуют разные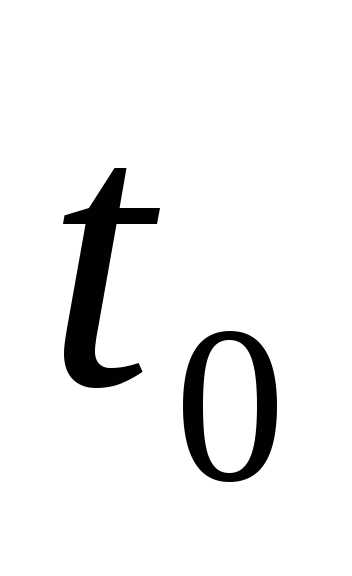 - значения времени начала процесса). При
- значения времени начала процесса). При численность остается постоянной, т.е. в этом случае решением уравнения является равновесная величина
численность остается постоянной, т.е. в этом случае решением уравнения является равновесная величина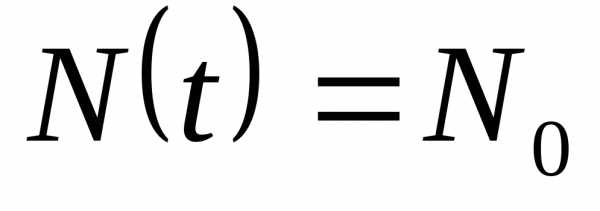 . Равновесие между рождаемостью и смертностью неустойчиво в том смысле, что даже небольшое нарушение равенства
. Равновесие между рождаемостью и смертностью неустойчиво в том смысле, что даже небольшое нарушение равенства  приводит с течением времени ко все большему отклонению функции
приводит с течением времени ко все большему отклонению функции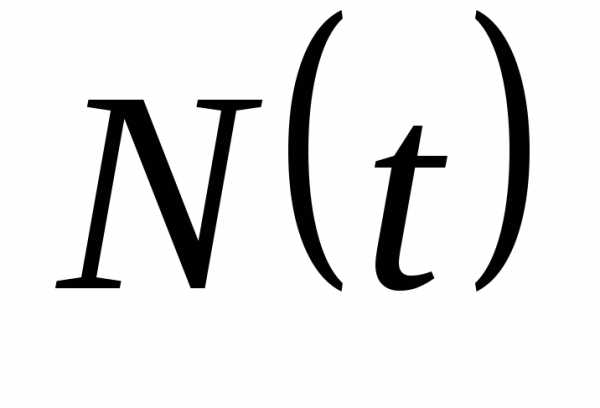 от равновесного значения
от равновесного значения 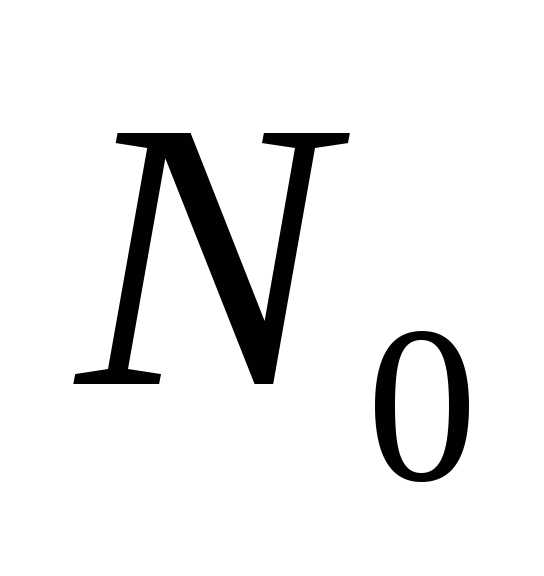 . При
. При 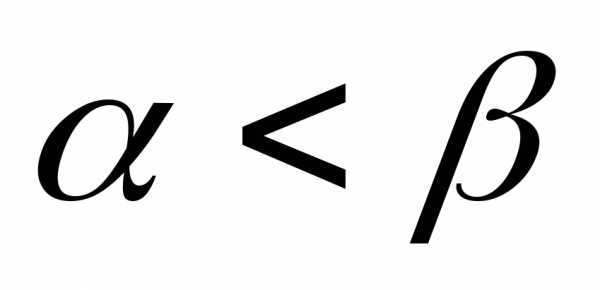 численность населения убывает и стремится к нулю при
численность населения убывает и стремится к нулю при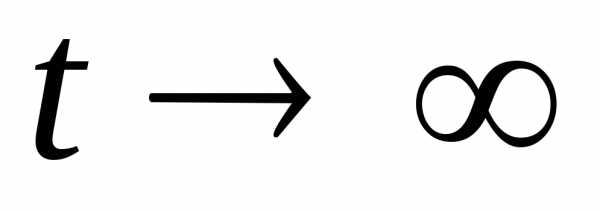 , а при
, а при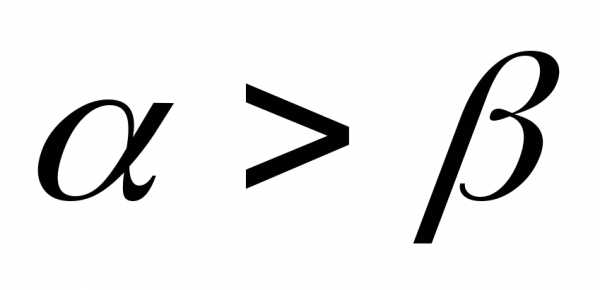 растет по экспоненциальному закону, обращаясь в бесконечность при
растет по экспоненциальному закону, обращаясь в бесконечность при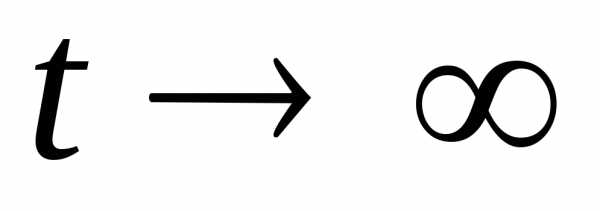 . Последнее обстоятельство и послужило основанием для опасений Мальтуса о грядущем перенаселении Земли со всеми вытекающими отсюда последствиями.
. Последнее обстоятельство и послужило основанием для опасений Мальтуса о грядущем перенаселении Земли со всеми вытекающими отсюда последствиями.
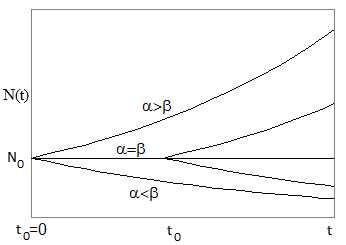
Рис.1.Изменение численности популяции со временем в модели Мальтуса
В данном примере можно указать немало очевидных ограничений применимости построенной модели. Конечно же, сложнейший процесс изменения численности населения, зависящий к тому же от сознательного вмешательства самих людей, не может описываться какими-либо простыми закономерностями. Даже в идеальном случае изолированной биологической популяции предложенная модель не отвечает реальности в полной мере хотя бы из-за ограниченности ресурсов, необходимых для ее существования.
Сделанное замечание тем не менее нисколько не умаляет роли аналогий в построении математических моделей очень сложных явлений. Применение аналогий основано на одном из важнейших свойств моделей - их универсальности, т.е. их приложимости к объектам принципиально различной природы. Так, предположения типа "скорость изменения величины (или некоторой функции от нее)" широко используется в далеких друг от друга областях знаний.
studfiles.net
лабор09_форм_угринович
Задание 1.
Построение и исследование физических моделей
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мяча в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на определенном расстоянии.
Качественная описательная модель.
Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
Мячик мал по сравнению с Землей, поэтому его можно считать материальной точкой;
Изменение высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g=9,8 м/с2и движение по оси ОУ можно считать равноускоренным;
Скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси ОХ можно считать равномерным.
Формальная модель. Для формализации модели обозначим величины:
начальную скорость мячика- V0
угол бросания мячика- α
высоту стенки- h
расстояние до стенки- s
Изобразим график движения мячика:
Используем известные из курса физики формулы равномерного и равноускоренного движения. При заданной начальной скоростиV0и угле бросания α значения координат дальности полета Х и высоты У от времени можно описать следующими формулами:
Чтобы определить, попадет ли мячик в стену, необходимо вычислить его координату Yв момент времени, когда он будет находиться на расстоянииs. Из первой формулы выражаем время, которое понадобится мячику, чтобы преодолеть расстояниеs:
Подставляем это значение времени tв формулу для вычисления координатыY. Получаемl- высоту мячика над землей на расстоянииs:
Формализуем условие попадания мячика в мишень. Попадание произойдет, если значение высоты lмячика будет удовлетворять условию неравенства:
Если l<0, то это означает «недолет», еслиl>h, то это означает «перелет».
Преобразуйте теперь формальную модель в компьютерную с использованием электронных таблиц Excel.
Модель «Движение тела, брошенного под углом к горизонту» в электронных таблицах
1. Для ввода начальной скорости будем использовать ячейку В1, а для ввода угла – ячейку В2.
2. Введем в ячейки А5:А18 значения времени с интервалом в 0,2 с.
3. В ячейки В5 и С5 введем формулы:
=$B$1*COS(РАДИАНЫ($B$2))*A5
=$B$1*SIN(РАДИАНЫ($B$2))*A5-4,9*A5*A5
4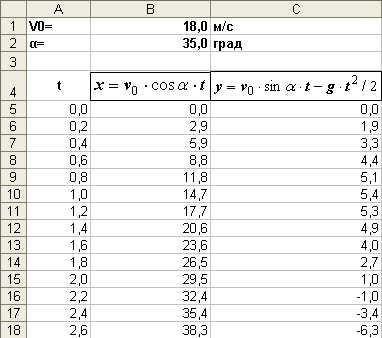 . Скопируем формулы в ячейки В6:B18 и С6:С18 соответственно.
. Скопируем формулы в ячейки В6:B18 и С6:С18 соответственно.
Визуализируем модель, построив график зависимости координаты у от координаты х (траекторию движения тела).
5. Построим диаграмму типа Точечная, в которой используется в качестве категории диапазон ячеек В5:В18, а в качестве значений – диапазон ячеек С5:С18.
Исследование модели. Исследуем модель и определим с заданной точностью 0,10диапазон изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии 30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/С. Воспользуемся для этого методомПодбор параметра.
1. Установить для ячеек точность один знак после запятой.
2. Ввести в ячейки В21, В22 и В23 значения расстояния до мишени S=30 м, начальной скоростиV0 = 18 м/с и угла α=350, а в ячейку В25 – формулудля вычисления высоты мячика над поверхностью для заданных начальных условий:
=В21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(В23))^2).
Для заданных начальных условий определим углы, которые обеспечивают попадание в мишень на высотах 0 и 1 м.
3. Выделим ячейку В25 и введем команду [Сервис-Подбор параметра…]. На появившейся диалоговой панели введем в поле Значение: наименьшую высоту попадания в мишень (то есть 0). В полеИзменяя значение ячейки: введем адрес ячейки, содержащей значение угла (в данном случай $B$23).
4. В ячейке В23 появится значение 32,6. Повторить процедуру подбора параметра для максимальной высоты попадания в мишень – в ячейке В23 получим значение 36,1.
Таким образом, исследование модели показало, что существует диапазон значений угла бросания мячика от 32,60 до 36,10, при котором обеспечивается попадание в стенку высотой 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.
Задание для самостоятельного выполнения:
определить диапазон предельных углов при начальном значении угла в ячейке B23, равном 550.
Вывести на одном графике траектории мячика для двух диапазонов углов бросания.
Задание 2.
Приближенное решение уравнений в электронных таблицах
Постановка задачи
Найти корень уравнения приближенными методами (графическим и с помощью методаПодбор параметра).
Компьютерная модель
Представить заданное уравнении в табличной форме:
Для грубо приближенного определения корня построить диаграмму типа Точечная.
По графику грубо приближенно можно определить, что 
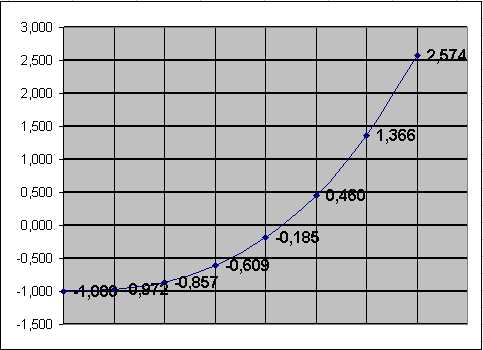
Для поиска решения с заданной точностью используем метод Подбор параметра. Точность подбора зависит от заданной точности представления чисел в ячейках таблицы (например, до трех знаков после запятой).
Методом подбора параметра необходимо определить значение аргумента  (ячейкаF1), при котором значение функции
(ячейкаF1), при котором значение функции  (ячейкаF2) будет равно нулю.
(ячейкаF2) будет равно нулю.
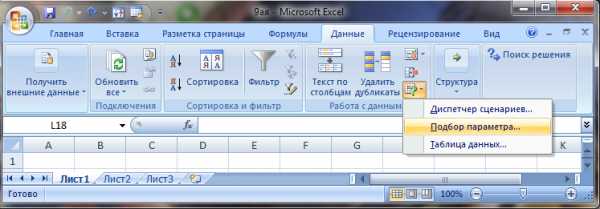
Выделить ячейку со значением функции F2 и ввести команду [На вкладке Данные в группе Средства обработки данных выберите команду Анализ условия, а затем выберите в списке пункт Подбор параметра.]
В диалоговом окне Подбор параметра:
в поле Установить в ячейке ввести адрес ячейки $F$2
в поле Значение ввести требуемое значение функции ( в данном случае 0)
в поле Изменяя значение ячейки ввести адрес ячейки $F$1, в которой будет производиться подбор значения аргумента
щелкнуть по кнопке ОК
На панели Результат подбора параметра будет выведена информация о величине значения в ячейке F2.
В ячейке аргумента F1 появится подобранное значение 0,855. Таким образом, корень уравнения найден с заданной точностью.
Задание для самостоятельного выполнения:
аналогичным способом решить уравнение
Задание 3.
Компьютерные модели развития популяций в электронных таблицах
Формальная модель
Начнём с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определённый процент. Математическую модель можно записать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента ростаa:
Например, если ежегодный прирост численности популяции составляет 5%, то a=1,05
В модели ограниченного ростаучитывается эффект перенаселённости, связанный с нехваткой питания, болезнями и так далее, который замедляет рост популяции с увеличением её численности.
Введём коэффициент перенаселённости b, значение которого обычно существенно меньшеa. Тогда коэффициент ежегодного увеличения численности равен
В модели ограниченного роста с отловом, учитывается, что на численность промысловых видов животных и рыб оказывает влияние величина ежегодного отлова. Формула принимает вид:
Популяции обычно взаимодействуют с другими популяциями, наиболее важным является взаимодействие между хищниками и жертвами. В модели «хищник- жертва»количество жертв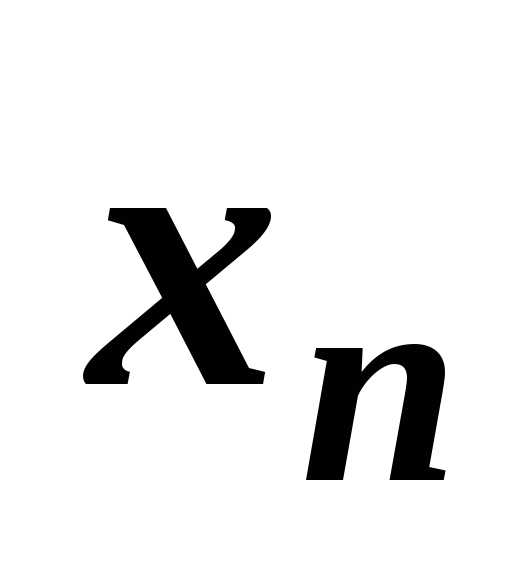 и количество хищников
и количество хищников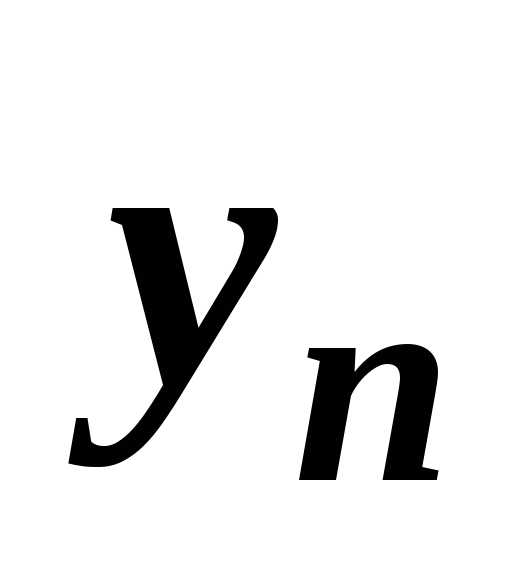 связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициентfхарактеризует возможность гибели жертвы при встрече с хищником. В этом случае численность популяции жертв уменьшается на величину
связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициентfхарактеризует возможность гибели жертвы при встрече с хищником. В этом случае численность популяции жертв уменьшается на величину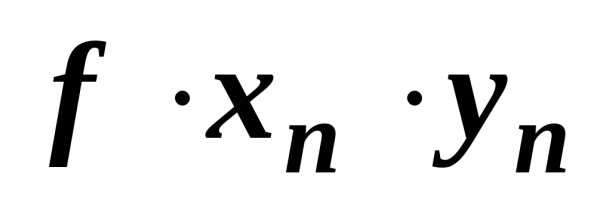 и формула для расчета численности жертв принимает вид:
и формула для расчета численности жертв принимает вид:
Численность популяции хищников в отсутствие жертв ( в связи с отсутствием пищи) уменьшается, что можно описать рекуррентной формулой
,
где значение коэффициента d<1 характеризует скорость уменьшения численности популяции хищников.
Увеличение популяции хищников можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент gхарактеризует величину роста численности хищников за счет жертв. Тогда для численности хищников можно использовать формулу:
Компьютерная модель
В столбцы AиBвнести начальные данные:
В столбце Dбудем вычислять численность популяции в соответствии с моделью неограниченного роста, в столбцеE– ограниченного роста, в столбцеF- ограниченного роста с отловом, в столбцахG,Hчисленность популяций жертв и хищников.
В ячейки D2,E2,F2,G2,h3 внести начальные значения численности популяций(для простоты - 1).
В D3 ввести формулу неограниченного роста:
=$B$2*D2
В E3 ввести формулу ограниченного роста:
=($b$2-$b$3*e2)*e2)
По этому принципу ввести формулы и в ячейки F3,G3,h4.
Заполнить ячейки на 25 позиций вниз.
Построить диаграмму типа График, отражающую все модели на одном графике.
Задание для самостоятельного выполнения:
1) исследовать модель и определить, через сколько лет произойдёт удвоение численности популяции в модели неограниченного роста.
2) в модели ограниченного роста с отловом установить предельное значение величины отлова при заданных значениях коэффициентов aиb (использовать методПодбор параметра). То есть определить при каком значенииc(полеИзменяя ячейку) численность популяции через 24 обратится в 0 (полеЗначение)
Задание 4.
Построение и исследование оптимизационной модели в электронных таблицах
Постановка задачи.
В ходе производственного процесса из листов материала получают заготовки деталей двух типов А и Б тремя различными способами, при этом количество получающихся заготовок при каждом методе различается.
| Тип заготовки | Количество заготовок | ||
| Способ раскроя 1 | Способ раскроя 2 | Способ раскроя 3 | |
| А | 10 | 3 | 8 |
| Б | 3 | 6 | 4 |
Необходимо выбрать оптимальное сочетание способов раскроя, для того чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.
Формальная модель
Параметрами, значения которых требуется определить, это количества листов материала, которые будут раскроены различными способами:
Х1-количество листов, раскроенное способом 1, Х2-количество листов, раскроенное способом 2, Х3-количество листов, раскроенное способом 3
Тогда целевая функция, значением которой является количество листов материала, равна F=X1+X2+X3
Ограничения определяются значениями требуемых количеств заготовок типа А и Б. То есть должны выполняться два равенства:
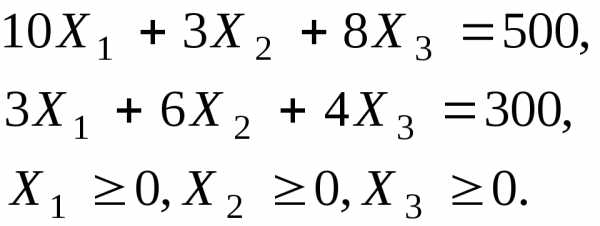
Компьютерная модель.
ЯчейкиB2,C2,D2 выделить для хранения значений параметровX1,X2 иX3.X1
X2
X3
Параметры
Целевая функция
Ограничения
Кол-во заготовок А
Кол-во заготовок Б
В ячейку B4 ввести формулу для вычисления целевой функции: =B2+C2+D2
В ячейку B7 ввести формулу вычисления количества заготовок типа А: =10*B2+3*C2+8*D2
В ячейку B8 ввести формулу вычисления количества заготовок типа Б: =3*B2+6*C2+4*D2
Выполнить команду Сервис- надстройки.Установить галочку напротив Поиск решения.
Выполнить команду Сервис- Поиск решения.
Установить:
Адрес целевой ячейки
Вариант оптимизации значения целевой ячейки (максимизация, минимизация или подбор значения)
Адреса ячеек, значения которых изменятся в процессе поиска решения
Ограничения (типа «=» для ячеек, хранящих количество деталей и типа «» для параметров,а также что искомые параметры- целые числа)
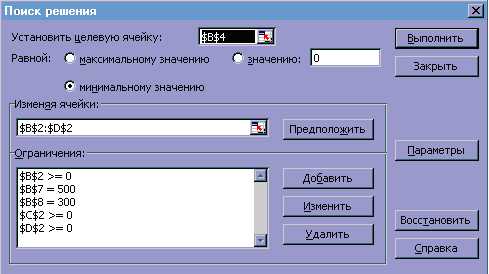
Должно получиться следующее: в ячейке целевой функции 70, а в ячейках параметров 20, 20, 30.
Задание для самостоятельного выполнения.
Решить аналогичным способом следующую задачу:
При получении школой нового компьютерного класса необходимо оптимально спланировать использование единственного легкового автомобиля для перевозки 15 компьютеров. Каждый компьютер упакован в две коробки (монитор и системный блок) и существуют три варианта погрузки коробок в автомобиль.
Способы погрузки
| Тип коробки | Варианты погрузки | ||
| 1 | 2 | 3 | |
| Мониторы | 3 | 2 | 1 |
| Системный блок | 1 | 2 | 4 |
Необходимо выбрать оптимальное сочетание вариантов погрузки для того, чтобы перевезти 15 коробок с мониторами и 15 коробок с системными блоками за минимальное количество рейсов автомобиля.
Формальная модель.
Параметрами, значения которых требуется определить, являются количества рейсов автомобиля, загруженного различными способами:
Х1- количество рейсов автомобиля, загруженного по варианту 1.
Х2-количество рейсов автомобиля, загруженного по варианту 2.
Х3- количество рейсов автомобиля, загруженного по варианту 3.
Тогда целевая функция, равная количеству рейсов автомобиля, примет вид:
F=X1+X2+X3.
Ограничения накладываются количествами коробок с мониторами и системными блоками, которые необходимо перевезти. Должны выполняться два равенства:
3*Х1+2*X2+1*X3=15
1*X1+2*X2+4*X3=15.
Кроме того, количества рейсов не могут быть отрицательными, поэтому должны выполняться неравенства:
X1≥0;X2≥0;X3≥0.
Таким образом, необходимо найти удовлетворяющие ограничениям значения параметров, при которых целевая функция принимает минимальное значение.
studfiles.net











