Научно-исследовательская работа по теме "Симметрия в природе". Центральная симметрия в растениях
Симметрия в мире растений - стр.2
СИММЕТРИЯ В МИРЕ РАСТЕНИЙ
Законы симметрии открывают пути к пониманию обобщающих геометрических законов морфологии растений.
Специфика строения растений и животных определяется особенностями среды обитания, к которой они приспосабливаются, особенностями их образа жизни. У любого дерева есть основание и вершина, "верх" и "низ", выполняющие разные функции. Значимость различия верхней и нижней частей, а также направление силы тяжести определяют вертикальную ориентацию поворотной оси "древесного конуса" и плоскостей симметрии. Для листьев характерна зеркальная симметрия. Эта же симметрия встречается и у цветов, однако у них зеркальная симметрия чаще выступает в сочетании с поворотной симметрией. Нередки случаи и переносной симметрии (веточки акации, рябины). Интересно, что в цветочном мире наиболее распространена поворотная симметрия 5-го порядка, которая принципиально невозможна в периодических структурах неживой природы. Этот факт академик Н. Белов объясняет тем, что ось 5-го порядка - своеобразный инструмент борьбы за существование, "страховка против окаменения, кристаллизации, первым шагом которой была бы их поимка решеткой". Действительно, живой организм не имеет кристаллического строения в том смысле, что даже отдельные его органы не обладают пространственной решеткой.
На рис. 11,а совокупность листьев при так называемом мутовчатом листорасположении не нарушает общей радиальной симметрии. Такие кольца из листьев совместно со стеблем подчиняются симметрии Ln nР. Совсем иная картина при очередном листорасположении. Здесь присутствуют винтовые оси2. Угол поворота винтовой оси называется «углом расхождения листьев». Вертикальная прямая, Рис.11 соединяющая два листа, расположенные друг над другом на стебле, именуется «ортостихой».
В ботанике принято характеризовать винтовое листорасположение с помощью дроби, числителем которой является число оборотов в листовом цикле, а знаменателем – число листьев в этом цикле. На рис. 11, б показана пятерная винтовая ось 1/5. ботаники утверждают, что дроби, характеризующие винтовые оси, образуют ряд, называемый в математике рядом Фибоначчи:
1/2, 1/3, 2/5, 3/8, 5/13, 8/21,…
Дроби, входящие в ряд Фибоначчи, замечательны тем, что сумма числителей двух соседних дробей дает числитель следующей дроби, так же как и сумма знаменателей пары смежных дробей равна знаменателю дроби, стоящей вслед за ними. Дроби листорасположения некоторых растений: ½ свойственна злакам, березе, винограду; 1/3 – осоке, тюльпану, ольхе; 2/5 – груше, смородине, сливе; 3/8 – капусте, редьке, льну; 5/13 – ели, жасмину.
Винтовые оси на стеблях нагляднее всего демонстрируют существование правых и левых растений.
СИММЕТРИЯ В МИРЕ ЖИВОТНЫХ
Ось симметрии. Ось симметрии - это ось вращения. В этом случае у животных, как правило, отсутствует центр симметрии. Тогда вращение может происходить только вокруг оси. При этом ось чаще всего имеет разнокачественные полюса. Например, у кишечнополостных, гидры или актинии, на одном полюсе расположен рот, на другом - подошва, которой эти неподвижные животные прикреплены к субстрату (рис.12(1,2,3)). Ось симметрии может совпадать морфологически с переднезадней осью тела.
Плоскость симметрии. Плоскость симметрии - это плоскость, проходящая через ось симметрии, совпадающая с ней и рассекающая тело на две зеркальные половины. Эти половины, расположенные друг против друга, называют антимерами (anti – против; mer – часть). Например, у гидры плоскость симметрии должна пройти через ротовое отверстие и через подошву. Антимеры противоположных половин должны иметь равное число щупалец, расположенных вокруг рта гидры. У гидры можно провести несколько плоскостей симметрии, число которых будет кратно числу щупалец. У актиний с очень большим числом щупалец можно провести много плоскостей симметрии. У медузы с четырьмя щупальцами на колоколе число плоскостей симметрии будет ограничено числом, кратным четырём. У гребневиков только две плоскости симметрии - глоточная и щупальцевая (рис.12,5). Наконец, у двусторонне-симметричных организмов только одна плоскость и только две зеркальные антимеры – соответственно правая и левая стороны животного (рис.12(4,6,7)).
Типы симметрии у животных
| 1-центральная | 2-осевая | 3-радиальная | 4-билатеральная |
|
| |||
| 5-двулучевая | 6-поступательная (метамерия) | 7-поступательно-вращательная | |
Рис. 12
Типы симметрии. Известны всего два основных типа симметрии – вращательная и поступательная. Кроме того, встречается модификация из совмещения этих двух основных типов симметрии – вращательно-поступательная симметрия.
Вращательная симметрия. Любой организм обладает вращательной симметрией. Для вращательной симметрии существенным характерным элементом являются антимеры. Важно знать, при повороте на какой градус контуры тела совпадут с исходным положением. Минимальный градус совпадения контура имеет шар, вращающийся около центра симметрии. Максимальный градус поворота - 360º, когда при повороте на эту величину контуры тела совпадут. Если тело вращается вокруг центра симметрии, то через центр симметрии можно провести множество осей и плоскостей симметрии. Если тело вращается вокруг одной гетерополярной оси, то через эту ось можно провести столько плоскостей, сколько антимер имеет данное тело. В зависимости от этого условия говорят о вращательной симметрии определённого порядка. Например, у шестилучевых кораллов будет вращательная симметрия шестого порядка. У гребневиков две плоскости симметрии, и они имеют симметрию второго порядка. Симметрию гребневиков также называют двулучевой (рис.12,5). Наконец, если организм имеет только одну плоскость симметрии и соответственно две антимеры, то такую симметрию называют двусторонней или билатеральной (рис.12,4). Лучеобразно отходят тонкие иглы. Это помогает простейшим «парить» в толще воды. Шарообразны и другие представители простейших – лучевики (радиолярии) и солнечники с лучевидными отростками-псевдоподиями. «Глядя на них, так и кажется, что эти кружевные сплетения – не часть живых существ, а тончайшие ювелирные изделия, предназначенные украшать наряды морских.
Поступательная симметрия. Для поступательной симметрии характерным элементом являются метамеры (meta – один за другим; mer – часть). В этом случае части тела расположены не зеркально друг против друга, а последовательно друг за другом вдоль главной оси тела.
Метамерия – одна из форм поступательной симметрии. Она особенно ярко выражена у кольчатых червей, длинное тело которых состоит из большого числа почти одинаковых сегментов. Этот случай сегментации называют гомономной (рис.12, 6 ). У членистоногих животных число сегментов может быть относительно небольшим, но каждый сегмент несколько отличается от соседних или формой, или придатками ( грудные сегменты с ногами или крыльями, брюшные сегменты). Такую сегментацию называют гетерономной.
Вращательно-поступательная симметрия. Этот тип симметрии имеет ограниченное распространение в животном мире. Эта симметрия характерна тем, что при повороте на определённый угол часть тела немного проступает вперед и её размеры каждый следующий логарифмически увеличивает на определённую величину. Таким образом, происходит совмещение актов вращения и поступательного движения. Примером могут служить спиральные камерные раковины фораминифер, а также спиральные камерные раковины некоторых головоногих моллюсков (современный наутилус или ископаемые раковины аммонитов, рис. 12, 7). С некоторым условием к этой группе можно отнести также и некамерные спиральные раковины брюхоногих моллюсков.
Тип симметрии непременно входит в характеристику животных наряду с другими морфоэкологическими и физиологическими признаками, благодаря которым мы отличаем одни группы животных от других.
Всех животных делят на одноклеточных и многоклеточных. Наличие форм симметрии прослеживается уже у простейших – одноклеточных (инфузории, амёбы). Многоклеточные подразделяются на Лучистых и Двусторонне-симметричных или Билатеральных.
Значение формы симметрии для животного легко понять, если поставить её в связь с образом жизни, экологическими условиями3. Рассмотрим ещё один тип симметрии, который встречается в животном мире. Это винтовая или спиральная симметрия. Винтовая симметрия есть симметрия относительно комбинации двух преобразований - поворота и переноса вдоль оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта. Встречаются левые и правые винты. Примерами природных винтов являются: бивень нарвала (небольшого китообразного, обитающего в северных морях) – левый винт; раковина улитки – правый винт; рога памирского барана – энантиоморфы (один рог закручен по левой, а другой по правой спирали). Спиральная симметрия не бывает идеальной, например, раковина у моллюсков сужается или расширяется на конце.
Хотя внешняя спиральная симметрия у многоклеточных животных встречается редко, зато спиральную структуру имеют многие важные молекулы, из которых построены живые организмы – белки, дезоксирибонуклеиновые кислоты – ДНК4.
Отметим, наконец, билатеральную симметрию человеческого тела (речь идёт о внешнем облике и строении скелета). Эта симметрия всегда являлась и является основным источником нашего эстетического восхищения хорошо сложенным человеческим телом. Наша собственная зеркальная симметрия очень удобна для нас, она позволяет нам двигаться прямолинейно и с одинаковой лёгкостью поворачиваться вправо и влево. Столь же удобна зеркальная симметрия для птиц, рыб и других активно движущихся существ.
ПРИШЕЛЬЦЫ ИЗ ДРУГИХ МИРОВ
Во многих фантастических произведениях обсуждается возможный облик пришельцев из других миров. Одни писатели считают, что пришельцы могут сильно отличаться по своему облику от людей; другие, напротив, полагают, что разумные существа во всей Вселенной должны походить друг на друга. Не останавливаясь подробно на обсуждении этого вопроса, приведу лишь некоторые соображения, связанные с симметрией. Каким бы не был пришелец, его внешний облик должен характеризоваться билатеральной симметрией: ведь на любой планете живое существо должно иметь выделенное направление движения и на любой планете действует сила тяжести. Пришелец может походить на сказочного дракона, но он не может походить на Тянитолкая. Он не может быть левоглазым или правоухим. Число конечностей слева и справа должно быть одинаковым. Требования симметрии позволяют существенным образом сократить число возможных вариантов облика пришельцев. И хотя мы не можем определенно указать, каким должен быть этот облик, мы в состоянии заключить, каким он не может быть.
ЗНАЧЕНИЕ СИММЕТРИИ В ПОЗНАНИИ ПРИРОДЫ
Идея симметрии часто являлась отправным пунктом в гипотезах и теориях ученых прошлого. Вносимая симметрией упорядоченность проявляется, прежде всего, в ограничении многообразия возможных структур, в сокращении числа возможных вариантов. В качестве важного физического примера можно привести факт существования определяемых симметрией ограничений разнообразия структур молекул и кристаллов. Поясним эту мысль на следующем примере. Допустим, что в некоторой отдаленной галактике обитают высокоразвитые существа, увлекающиеся среди прочих занятий также играми. Мы можем ничего не знать о вкусах этих существ, о строении их тела и особенностях психики. Однако достоверно, что их игральные кости имеют одну из пяти форм - тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Всякая иная форма игральной кости в принципе исключена, поскольку требование равновероятности выпадения при игре любой грани предопределяет использование формы правильного многогранника, а таких форм только пять.
Идея симметрии часто служила ученым путеводной нитью при рассмотрении проблем мироздания. Наблюдая хаотическую россыпь звезд на ночном небе, мы понимаем, что за внешним хаосом скрываются вполне симметричные спиральные структуры галактик, а в них – симметричные структуры планетных систем. Симметрия внешней формы кристалла является следствием ее внутренней симметрии – упорядоченного взаимного расположения в пространстве атомов (молекул). Иначе говоря, симметрия кристалла связана с существованием пространственной решетки из атомов, так называемой кристаллической решетки.
Согласно современной точке зрения, наиболее фундаментальные законы природы носят характер запретов. Они определяют, что может, а что не может происходить в природе. Так, законы сохранения в физике элементарных частиц запрещают любое явление, при котором изменялась бы "сохраняющаяся величина", являющаяся собственной «абсолютной» константой (собственным значением) соответствующего объекта и характеризующая его «вес» в системе других объектов. И эти значения являются абсолютными до тех пор, пока такой объект существует.
Всеобщность симметрии не только в том, что она обнаруживается в разнообразных объектах и явлениях. Всеобщим является сам принцип симметрии, без которого по сути дела нельзя рассмотреть ни одной фундаментальной проблемы, будь то проблема жизни или проблема контактов с внеземными цивилизациями.
Принципы симметрии лежат в основе теории относительности, квантовой механики, физики твердого тела, атомной и ядерной физики, физики элементарных частиц. Эти принципы наиболее ярко выражаются в свойствах инвариантности законов природы. Речь при этом идет не только о физических законах, но и других, например, биологических.
Примером биологического закона сохранения может служить закон наследования. В основе его лежат инвариантность биологических свойств по отношению к переходу от одного поколения к другому. Вполне очевидно, что без законов сохранения (физических, биологических и прочих) наш мир попросту не смог бы существовать.
ЗАКЛЮЧЕНИЕ
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. В своем реферате я показала, что законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии как в растительном, так и в животном мире, но я считаю, что при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира. Еще одним интересным проявлением симметрии жизненных процессов являются биологические ритмы (биоритмы), циклические колебания биологических процессов и их характеристик (сокращения сердца, дыхание, колебания интенсивности деления клеток, обмена веществ, двигательной активности, численности растений и животных), зачастую связанные с приспособлением организмов к геофизическим циклам. Исследованием биоритмов занимается особая наука - хронобиология.
В моей работе отмечено так же, что помимо симметрии существует понятие асимметрии. Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.
Работая над рефератом, я поняла слова видного ученого академика В. И. Вернадского, который писал в 1927 году: "Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности". Действительно, всеобщность симметрии поразительна. Симметрия устанавливает внутренние связи между объектами и явлениями, которые внешне никак не связаны.
ЛИТЕРАТУРА:
1. Гильде В. Зеркальный мир. — М.: Мир, 1982.
2. Современный словарь иностранных слов. — М.: Русский язык, 1993.
3. Советский энциклопедический словарь — М.: Советская энциклопедия, 1980.
4. Урманцев Ю.А. Симметрия природы и природа симметрии — М.: Мысль, 1974
5. Шафрановский И.И. Симметрия в природе. –Л.: Недра, 1985.
Приложение 1
| Соты- настоящий конструкторский шедевр. Они состоят из ряда симметричных шестигранных ячеек. | |
| Это самая плотная упаковка, позволяющая наивыгоднейшим образом разместить в ячейке личинку и при максимально возможном объеме наиболее экономно использовать строительный материал-воск. | |
Приложение 2
| Листья на стебле расположены не по прямой, а окружают ветку по спирали. Сумма всех предыдущих шагов спирали, начиная с вершины, равна величине последующего шага А+В=С, В+С=Д и т.д. | |
| Расположение семянок в головке подсолнуха или листьев в побегах вьющихся растений соответствует логарифмической спирали | |
Приложение 3
Значение формы симметрии для животного легко понять, если поставить её в связь с образом жизни, экологическими условиями.
Если окружающая животное среда со всех сторон более или менее однородна и животное равномерно соприкасается с нею всеми частями своей поверхности, то форма тела обычно шарообразна , а повторяющиеся части располагаются по радиальным направлениям. Шарообразны многие радиолярии, входящие в состав так называемого планктона, т.е. совокупности организмов, взвешенных в толще воды и неспособных к активному плаванию; шарообразные камеры имеют немногочисленные планктонные представители фораминифер. Лучевики - исключительно морские животные, ведущие планктонный образ жизни. Они «парят» в толще морской воды и идеально к этому приспособлены. Именно для этого «парения» служат иглы их скелета, увеличивающие площадь тела. Лучевики обладают минеральным сложно устроенным внутренним скелетом, который, с одной стороны, защищает тело простейшего, а с другой, способствует «парению» в воде в результате увеличения поверхности путём образования многочисленных игл. От тела во все стороны отходят многочисленные нитевидные отростки-псевдоподии. Солнечники, в общем, походят на лучевиков, но встречаются преимущественно в пресных водах. Шаровидное тело солнечников посылает во все стороны многочисленные тонкие, нитевидные радиально расположенные псевдоподии, тело лишено минерального скелета. Такой тип симметрии называют равноосным, так как он характеризуется наличием многих одинаковых осей симметрии. Равноосная симметрия должна превратиться в одноосную вместе с переходом к сидячему или мало подвижному донному образу жизни; если, например, шарообразное тело приобретает стебелёк для прикрепления к субстрату, то ось симметрии должна будет проходить через стебелёк и сделается, таким образом, единственной. Примерами такой симметрии могут служить сидячие солнечники, жгутиковые, сосущие инфузории, бокалообразные губки. Тот же результат может получиться и при отсутствии стебелька, если животное постоянно обращено одним полюсом к субстрату а другим кверху. При активном плавании одной стороною тела вперёд эта сторона также может дифференцироваться в передний конец тела, и симметрия сложится одноосная (например, овальные или веретенообразные жгутиковые и инфузории). Во всех этих случаях соединяемые осью полюса тела находятся в неодинаковых экологических условиях и функционируют по-разному. Присутствие одной только оси симметрии не столь ещё характерно для данного типа (так как и в других типах симметрии, кроме равноосного, ось также одна), но весьма характерно, то что через эту ось можно провести много плоскостей симметрии, из которых каждая разделит тело на две одинаковые половины; поэтому данный тип симметрии называют полисимметрическим. Равноосный и полисимметрический типы встречаются преимущественно среди низкоорганизованных и малодифференцированных животных. Сидячие одноосные полисимметрические животные, усложняя свою организацию и приобретая различные органы, приобретают лучевую или радиальную симметрию тела, выражающуюся в том, что органы располагаются в радиальных (лучистых) направлениях вокруг одной главной продольной оси. От числа повторяющихся органов зависит порядок радиальной симметрии. Так, если вокруг продольной оси располагается 4 одинаковых органа, то радиальная симметрия в этом случае называется четырёхлучевой. Если таких органов шесть, то и порядок симметрии будет шестилучевым, и т.д. Так как количество таких органов ограничено (часто 2,4,8 или кратное от 6), то и плоскостей симметрии можно провести всегда несколько, соответствующее количеству этих органов. Плоскости делят тело животного на одинаковые участки с повторяющимися органами. В этом заключается отличие радиальной симметрии от полисимметрического типа. Радиальная симметрия характерна для малоподвижных и прикрепленных форм (двух-, четырёх-, восьми – и шести -лучевые кораллы, гидра, медузы, актинии). Экологическое значение лучевой симметрии легко понятно: сидячее животное окружено со всех боковых сторон одинаковой средою и должно вступать во взаимоотношения с этой средой при помощи одинаковых, повторяющихся в радиальных направлениях органов. Именно сидячий образ жизни способствует развитию лучистой симметрии.
Переход от лучевой или радиальной к двусторонней или билатеральной симметрии связан с переходом от сидячего образа жизни к активному передвижению в среде (от сидячести к ползанию по субстрату постоянно одним и тем же концом тела вперёд). Для сидячих форм отношения со средой равноценны во всех направлениях: радиальная симметрия точно соответствует такому образу жизни. У активно перемещающихся животных передний конец тела становится биологически не равноценным остальной части туловища, происходит формирование головы, становятся различимы правая и левая сторона тела. Благодаря этому теряется радиальная симметрия , и через тело животного можно провести лишь одну плоскость симметрии, делящую тело на правую и левую стороны. Двусторонняя симметрия означает, что одна сторона тела животного представляет собой зеркальное отражение другой стороны. Такой тип организации характерен для большинства беспозвоночных, в особенности для кольчатых червей и для членистоногих – ракообразных, паукообразных, насекомых, бабочек; для позвоночных – рыб, птиц, млекопитающих. Впервые двусторонняя симметрия появляется у плоских червей, у которых передний и задний концы тела различаются между собой. У кольчатых червей и членистоногих наблюдается ещё и метамерия – одна из форм поступательной симметрии, когда части тела располагаются последовательно друг за другом вдоль главной оси тела. Особенно ярко она выражена у кольчатых червей (дождевой червь). Кольчатые черви обязаны своим названием тому, что их тело состоит из ряда колец или сегментов (члеников). Сегментированы как внутренние органы, так и стенки тела. Так что животное состоит примерно из сотни более или менее сходных единиц – метамеров, каждая из которых содержит по одному или по паре органов каждой системы. Членики отделены друг от друга поперечными перегородками. У дождевого червя почти все членики сходны между собой. К кольчатым червям относятся полихеты – морские формы, которые свободно плавают в воде, роются в песке. На каждом сегменте их тела имеется пара боковых выступов, несущих по плотному пучку щетинок. Членистоногие получили своё название за характерные для них членистые парные придатки (как органы плавания, ходильные конечности, ротовые части). Для всех них характерно сегментированное тело. Каждое членистоногое имеет строго определённое число сегментов, которое остаётся неизменным в течение всей жизни. Зеркальная симметрия хорошо видна у бабочки; симметрия левого и правого проявляется здесь с почти математической строгостью. Можно сказать, что каждое животное, насекомое, рыба, птица состоит из двух энантиоморфов – правой и левой половин. Так, энантиоморфами являются правое и левое ухо, правый и левый глаз, правый и левый рог и т.д.
Упрощение условий жизни может привести к нарушению двусторонней симметрии, и животные из двусторонне-симметричных становятся радиально-симметричными. Это относится к иглокожим (морские звёзды, морские ежи, морские лилии, офиуры). Все морские животные имеют радиальную симметрию, при которой части тела отходят по радиусам от центральной оси, подобно спицам колеса. Степень активности животных коррелирует с их типом симметрии. Радиально-симметричные иглокожие обычно мало подвижны, перемещаются медленно или же прикреплены к морскому дну. Тело морской звезды состоит из центрального диска и 5-20 или большего числа радиально отходящих от него лучей. На математическом языке эту симметрию называют поворотной симметрией. У морской звезды и панциря морского ежа – поворотная симметрия 5-го порядка (рис.1). Это симметрия, при которой объект совмещается сам с собой при повороте вокруг поворотной оси 5 раз. Вся кожа морских звёзд как бы инкрустирована мелкими пластинками из углекислого кальция, от некоторых пластинок отходят иглы, часть которых подвижна. У офиур лучи длинные и тонкие. Морские ежи похожи на живые подушечки для булавок; шаровидное тело их несёт длинные и подвижные иголки. У этих животных известковые пластинки кожи Рис. 1 слились и образовали сферическую раковину панцирь. В центре нижней поверхности имеется рот. Амбулакральные ножки (воднососудистая система) собраны в 5 полос на поверхности раковины.
Приложение 4
Подлинным царством природных винтов является мир «живых молекул» - молекул, играющих принципиально важную роль в жизненных процессах. К таким молекулам относятся прежде всего молекулы белков. В человеческом теле насчитывают до 10 типов белков. Все части тела, включая кости, кровь, мышцы, сухожилия, волосы, содержат белки. Молекула белка представляет собой цепочку, составленную из отдельных блоков, и закрученную по правой спирали. Её называют альфа-спиралью. За открытие альфа-спирали американский учёный Лайнус Полинг получил Нобелевскую премию, самую высшую награду в научном мире. Молекулы волокон сухожилий представляют собой тройные альфа-спирали. Скрученные многократно друг с другом альфа-спирали образуют молекулярные винты, которые обнаруживаются в волосах, рогах, копытах.
Исключительно важную роль в мире живой природы играют молекулы дезоксирибонуклеиновой кислоты – ДНК, являющейся носителем наследственной информации в живом организме. Молекула ДНК имеет структуру двойной правой спирали, открытой американскими учёными Уотсоном и Криком. За её открытие они были удостоены Нобелевской премии. Двойная спираль молекулы ДНК есть главный природный винт.
1 См. Приложение 1
2 См. Приложение 2
3 См. Приложение 3
4 См. Приложение 4
refdb.ru
Проект Цветочная геометрия / Понятие симметрии — Letopisi.ru
Материал из Letopisi.Ru — «Время вернуться домой»
Понятие симметрии проходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого организма, а именно человека. И употреблялось скульпторами ещё в 5 веке до н. э.
Слово "симметрия" греческое, оно означает "соразмерность, пропорциональность, одинаковость в расположении частей". Его широко используют все без исключения направления современной науки. Об этой закономерности задумывались многие великие люди. Например, Л. Н. Толстой говорил: "Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?". Действительно симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, - всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии. Герман Вейль сказал: "Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство". Герман Вейль - это немецкий математик. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким образом, математически строгое представление сформировалось сравнительно недавно - в начале ХХ века. Оно достаточно сложное. Мы же обратимся и еще раз вспомним те определения, которые даны нам в учебнике.
Ботаника - наука о растениях. Она охватывает огромный круг проблем: их систематику; развитие в течение геологического времени; возможности хозяйственного использования растений; закономерности внешнего и внутреннего строения растений.
Поиск закономерностей внешнего строения растений вопрос возник ещё в 5 веке до н. э. На явление симметрии в живой природе обратили внимание в Древней Греции пифагорейцы в связи с развитием ими учения о гармонии. В 19 веке появлялись отдельные работы, касающиеся этой темы. А в 1961 году как результат многовековых исследований, посвященных поиску красоты и гармонии окружающей нас природы, появилась наука биосимметрика.
Центральная симметрия наиболее характерна для цветов и плодов растений. Центральная симметрия характерна для различных плодов, в том числе для ягод: голубика, черника, вишня, клюква. Рассмотрим разрез любой из этих ягод. В разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии. Центральную можно наблюдать на изображении следующих цветов: цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки, а в некоторых центральной симметрией обладает и изображение всего цветка ромашки. На данном рисунке представлена ромашка .Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. Весь же цветок обладает центральной симметрией только в случае четного количества лепестков. В случае же нечетного количества лепестков, вспомните анютины глазки , он обладает только осевой.
В любом растении можно найти какую-то его часть, обладающую осевой или центральной симметрией. Это могут быть листья, цветы, стебли, стволы деревьев, плоды, и более мелкие части, такие как сердцевина цветка, пестик, тычинки и другие.
Осевая симметрия присуща различным видам растений и грибам, и их частям. Центральная симметрия наиболее характерна для плодов растений и некоторых цветов. Симметрию живого существа определяет направление его движения. Для живых существ, для которых ведущим направлением является направление движения "вперед", наиболее характерна осевая симметрия. Так как в этом направлении животные устремляются за пищей и в этом же спасаются от преследователей. А нарушение симметрии привело бы к торможению одной из сторон и превращению поступательного движения в круговое.
симметрия присутствует и в прошлом и в будущем. Симметрия - это не только математическое понятие. Его заимствовали из природы. А так как человек - это часть природы, то человеческое творчество во всех его проявлениях тяготеет к симметрии. Симметрия в живой природе: в животном и растительном мире, - передается генетически из поколения в поколение.
Использованные интернет – ресурсы:
[[Категория:?
letopisi.org
Центральная симметрия – источник жизни :: SYL.ru
Если б не было симметрии, как бы выглядел наш мир? Что считалось бы эталоном красоты и совершенства? Что значит для нас центральная симметрия и какую роль она играет? Между прочим, одну из самых значительных. Чтобы это понять, познакомимся с естественным законом природы ближе.
Центральная симметрия
Для начала определимся в понятии. Что мы подразумеваем под словосочетанием «центральная симметрия»? Это соразмерность, соотношение, пропорциональность, точная аналогичность сторон или частей чего-либо относительно условной или вполне определенной стержневой оси.
Центральная симметрия в природе
Симметрию можно найти всюду, если пристально присмотреться к окружающей нас действительности. Она присутствует в снежинках, листьях деревьев и трав, насекомых, цветах, животных. Центральная симметрия растений и живых организмов полностью определена влиянием внешней среды, которая до сих пор формирует обличье обитателей планеты Земля.
Флора
Вы любите собирать грибы? Тогда вы знаете, что гриб, разрезанный по вертикали, имеет ось симметрии, вдоль которой он формируется. То же явление вы можете наблюдать и у круглых центрально-симметричных ягод. А как красиво яблоко в разрезе! Причем абсолютно в каждом растении есть какая-либо часть, развившаяся по законам симметрии.
Фауна
Чтобы заметить симметрию насекомых, их, к счастью, анатомировать не надо. Бабочки, стрекозы – словно ожившие и порхающие цветы. Грациозные хищники и домашние кошечки… Можно бесконечно восхищаться творениями природы.
Водный мир
Сколь безгранично видовое разнообразие обитателей водной среды, столь часто там встречается центральная симметрия. Наверняка каждый сможет привести несколько простых примеров.
Центральная симметрия в жизни
На протяжении своей многовековой истории от древних храмов, средневековых замков и до современности человек познавал красоту, гармонию и учился созиданию, наблюдая за природой. Урбанистический мир, в котором живет большинство населения земли, полон симметрии. Это дома, техника, предметы быта, науки и искусства. Аналогия – залог успеха любого инженерного сооружения.
Симметрия в искусстве
Центральная симметрия – понятие не только математическое. Она присутствует во всех сферах жизни человека. Гармония ритмичной композиции никогда не оставляла человека равнодушным. Отражение этих принципов можно обнаружить в декоративно-прикладном искусстве: вышивке аутентичных мастериц совершенно разных народов, узорной резьбе по дереву, самотканых коврах. Равномерное построение повторов есть даже в устном песенном творчестве и искусстве стихосложения! И, конечно, украшения умельцы делали по тем же законам центральной симметрии. Именно тогда убранство принимает индивидуальность, неповторимую красоту и становится настоящим произведением искусства. Так симметрия воспитывает человечество, открывая волшебный принцип порядка, гармонии и совершенства.
www.syl.ru
Научно-исследовательская работа по теме "Симметрия в природе"
Муниципальное казенное общеобразовательное учреждение
Большевистская средняя общеобразовательная школа
НАУЧНО - ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
по теме:
«Симметрия в природе»
Выполнила: Берсенева Виктория Владимировна - ученица 9 класса Большевистской СОШ
Руководитель: Фаляхова Людмила Леонидовна – учитель математики
с. Сарапулка, 2015
Содержание
Введение…………………………………………………………………………..3
Раздел I. Симметрия в математике………………………………………………4
Глава 1. Центральная симметрия………………………………………………..5
Глава 2. Осевая симметрия………………………………………………………7
Глава 4. Зеркальная симметрия…………………………………………………8
Раздел II. Симметрия в живой природе……………………………………… 11
Глава 1. Симметрия в живой природе. Асимметрия и симметрия……… 11
Глава 2. Симметрия растений…………………………………………………14
Глава 3. Симметрия животных………………………………………………….16
Глава 4. Человек – существо симметричное…………………………………...18
Заключение……………………………………………………………………….21
Литература……………………………………………………………………….22
2
«Природа формулирует свои законы
языком математики…»
Галилео Галилей
Введение
Я люблю свое село Сарапулку, протекающую реку Иня. С удовольствием фотографирую растения , животных, всю природу в окрестностях села. После изучения темы в геометрии «Осевая и центральная симметрия» я обратила внимание, что на фотографиях цветы растения животные симметричны и решила исследовать и узнать принципы симметрии, её виды, разнообразие её в живой и неживой природе.
Под симметрией (от греч. symmetria — соразмерность) в широком смысле понимают правильность в строении тела и фигуры. Учение о симметрии представляет собой большую и важную ветвь тесно связанную с науками разных отраслей. С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Так, фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях. Симметричны многие детали механизмов, например, зубчатые колеса.
Было интересно, потому что данная тема затрагивает не только математику, хотя она и лежит в её основе, но и другие области науки, техники, природы. Симметрия, как мне кажется, является фундаментом природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений людей. Я обратила внимание на то, что во многих вещах, в основе красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды — от простейших, до самых сложных. Можно говорить о симметрии, как о гармонии пропорций, как о «соразмерности», регулярности и упорядоченности.
3
Нам это важно, потому что для многих людей математика – скучная и сложная наука, но для меня математика – не только цифры, уравнения и решения, но и красота в строении геометрических тел, живых организмов и даже является фундаментом для многих наук.
Цели исследовательской работы:
раскрыть особенности видов симметрии в природе;
показать всю привлекательность математики, как науки и её взаимосвязь с природой в целом.
Задачи:
подбор материала по симметрии, исследование и его обработка данных;
Систематизация и обобщение собранного материала;
выводы о проделанной работе;
оформление обобщенного материала.
4.
Раздел I. Симметрия в математике
Глава 1. Центральная симметрия
Понятие центральной симметрии следующее: «Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О, называется центром симметрии фигуры». Поэтому говорят, что фигура обладает центральной симметрией.
Понятия центра симметрии в «Началах» Евклида нет, однако в 38-ом предложении XI книги содержится понятие пространственной оси симметрии. Впервые понятие центра симметрии встречается в XVI в. В одной из теорем Клавиуса, гласящей: «если параллелепипед рассекается плоскостью, проходящей через центр, то он разбивается пополам и, наоборот, если параллелепипед рассекается пополам, то плоскость проходит через центр». Лежандр, который впервые ввёл в элементарную геометрию элементы учения о симметрии, показывает, что у прямого параллелепипеда имеются 3 плоскости симметрии, перпендикулярные к ребрам, а у куба 9 плоскостей симметрии, из которых 3 перпендикулярны к рёбрам, а другие 6 проходят через диагонали граней.



Евклид Симметрия в архитектуре Лежандр
5
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией. Однако, в отличие от окружности и параллелограмма, которые имеют только один центр симметрии, у прямой их бесконечно много – любая точка прямой является её центром симметрии. Примером фигуры, не имеющей центра симметрии, является произвольный треугольник.
В алгебре при изучении чётных и нечётных функций рассматриваются их графики. График чётной функции при построении симметричен относительно оси ординат, а график нечётной функции – относительно начала координат, т.е. точки О. Значит, нечётная функция обладает центральной симметрией, а чётная функция – осевой.
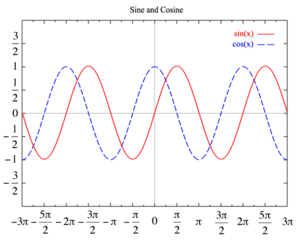
Таким образом, две центрально симметричные плоские фигуры всегда можно наложить друг на друга, не выводя их из общей плоскости. Для этого достаточно одну из них повернуть на угол 180° около центра симметрии. Как в случае зеркальной, так и в случае центральной симметрии плоская фигура непременно имеет ось симметрии второго порядка, но в первом случае эта ось лежит в плоскости фигуры, а во втором – перпендикулярна к этой плоскости. 6.
Глава 2. Осевая симметрия
Понятие осевой симметрии представлено следующим образом: «Фигура называется симметричной относительно прямой m, если для каждой точки фигуры симметричная ей точка относительно прямой, m также принадлежит этой фигуре. Прямая m, называется осью симметрии фигуры». Тогда говорят, что фигура обладает осевой симметрией
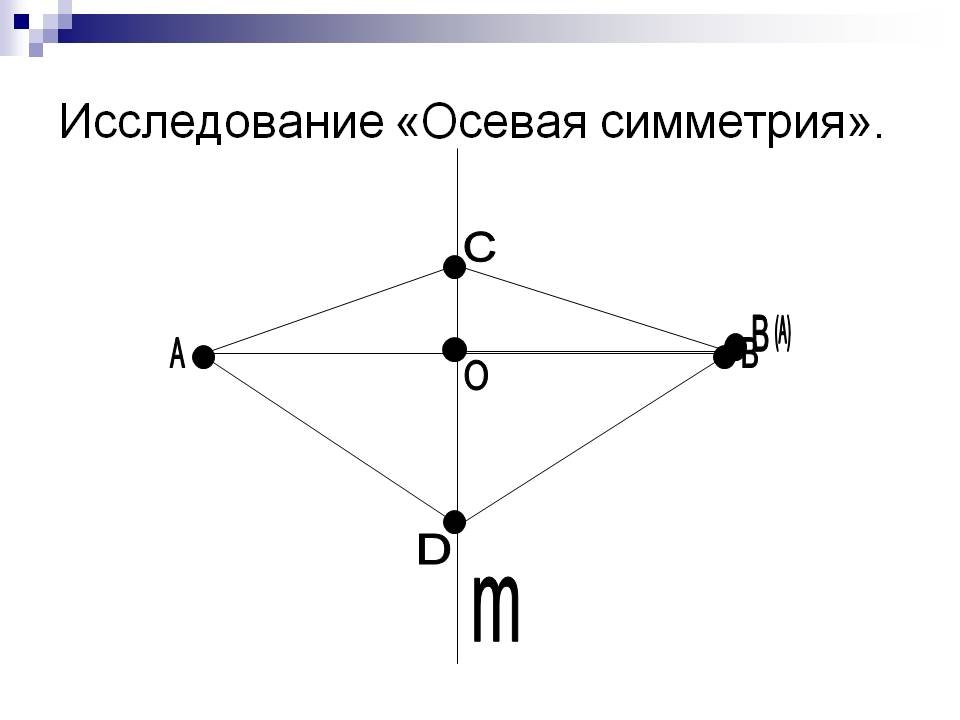
В более узком смысле осью симметрии называют ось симметрии второго порядка и говорят об «осевой симметрии», которую можно определить так: фигура (или тело) обладает осевой симметрией относительно некоторой оси, если каждой её точке С, соответствует такая принадлежащая этой же фигуре точка Д, что отрезок АВ перпендикулярен к оси, пересекает её и в точке пересечения делится пополам. Рассмотренная выше пара треугольников обладает (кроме центральной) еще осевой симметрией. Её ось симметрии проходит через точку О перпендикулярно к плоскости чертежа.
Приведём примеры фигур, обладающих осевой симметрией. У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла.
7.
Равнобедренный (но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по
две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконечно много — любая прямая, проходящая через её центр, является осью симметрии.

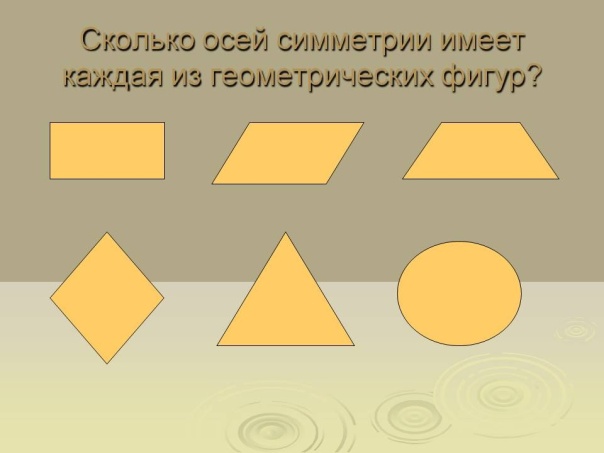
Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.
Глава 3. Зеркальная симметрия
Зеркальная симметрия хорошо знакома каждому человеку из повседневного наблюдения. Как показывает само название, зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело).
Я очень люблю фотографировать природу. Наше село расположено вдоль реки Иня. И когда весной разливается река, то на дальних лугах можно увидеть красивую картину, когда в воде отражаются: облака, лес, трава.
8

О нашей природе пишут стихи, рассказы. Одним из воспевателей был Анатолий Перович Бондарев. Он родился в Сарапулке, жил, рос. Много стихов написал, некоторые впоследствии стали песнями.


Дальние луга залитые водой Отражение заката в пруду


Река Иня Сельский пруд вблизи с. Сарапулка
Песня о родном селе
Сарапулка моя- Солнце пламенем жжет
Дорогое село, А река холодит,
Радость, горе, нужда- И пчела на цветок
Все быльем поросло. За пыльцою летит.
Я пою о селе, Окунусь с головой
Где родился и рос, В рябь лазури –реки,
Где мужал и взрослел, Полетят над волною
Где ходил на покос. Брызги , как мотельки
Запах свежей травы И на дальних лугах
На покосе полей, Как в перине посплю,
Звонкий смех детворы И в лесных родниках
У седых тополей Жажду я утолю.
Игрокам в бильярд издавна знакомо действие отражения. Их «зеркала» — это борта игрового поля, а роль луча света исполняют траектории шаров. Ударившись о борт возле угла, шар катится к стороне, расположенной под прямым углом, и, отразившись от неё, движется обратно параллельно направлению первого удара.
Важно отметить, что два симметричных друг другу тела не могут быть вложены или наложены друг на друга. Так перчатку правой руки нельзя надеть на левую руку. Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Чтобы убедиться в этом, достаточно поднести лист бумаги к зеркалу и попытаться прочесть несколько слов, напечатанных на ней, буквы и слова просто-напросто будут перевёрнуты справа налево. По этой причине симметричные предметы нельзя называть равными, поэтому их называют зеркально равными.
Две зеркально симметричные плоские фигуры всегда можно наложитьдруг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости. Вообще зеркально равными телами (или фигурами) называются тела (или фигуры) в том случае, если при надлежащем их смещении они могут образовать две половины зеркально симметричного тела (или фигуры).
Раздел II. Симметрия в живой природе
Глава 1. Симметрия в живой природе. Асимметрия и симметрия
Симметрией обладают объекты и явления живой природы. Она не только радует глаз и вдохновляет поэтов всех времен и народов, а позволяет живым организмам лучше приспособиться к среде обитания и просто выжить.
В живой природе огромное большинство живых организмов обнаруживает различные виды симметрии (формы, подобия, относительного расположения). Причем организмы разного анатомического строения могут иметь один и тот же тип внешней симметрии.
Внешняя симметрия может выступить в качестве основания классификации организмов (сферическая, радиальная, осевая и т.д.) Микроорганизмы, живущие в условиях слабого воздействия гравитации, имеют ярко выраженную симметрию формы.
Асимметрия присутствует уже на уровне элементарных частиц и проявляется в абсолютном преобладании в нашей Вселенной частиц над античастицами. Известный физик Ф. Дайсон писал: "Открытия последних десятилетий в области физики элементарных частиц заставляют нас обратить особое внимание на концепцию нарушения симметрии. Развитие Вселенной с момента ее зарождения выглядит как непрерывная последовательность нарушений симметрии. В момент своего возникновения при грандиозном взрыве Вселенная была симметрична и однородна. По мере остывания в ней нарушается одна симметрия за другой, что создает возможности для существования все большего и большего разнообразия структур. Феномен жизни естественно вписывается в эту картину. Жизнь - это тоже нарушение симметрии"
Молекулярная асимметрия открыта Л. Пастером, который первым выделил "правые" и "левые" молекулы винной кислоты: правые молекулы похожи на правый винт, а левые - на левый. Такие молекулы химики называют стереоизомерами.
Молекулы стереоизомеры имеют одинаковый атомный состав, одинаковые размеры, одинаковую структуру - в то же время они различимы, поскольку являются зеркально асимметричными, т.е. объект оказывается нетождественным со своим зеркальным двойником. Поэтому здесь понятия "правый-левый" - условны.
В настоящее время хорошо известно, что молекулы органических веществ, составляющие основу живой материи, имеют асимметричный характер, т.е. в состав живого вещества они входят только либо как правые, либо как левые молекулы. Таким образом, каждое вещество может входить в состав живой материи только в том случае, если оно обладает вполне определенным типом симметрии. Например, молекулы всех аминокислот в любом .живом организме могут быть только левыми, сахара ~ только правыми. Это свойство живого вещества и его продуктов жизнедеятельности называют дисимметрией. Оно имеет совершенно фундаментальный характер. Хотя правые и левые молекулы неразличимы по химическим свойствам, живая материя их не только различает, но и делает выбор. Она отбраковывает и не использует молекулы, не обладающие нужной ей структурой. Как это происходит, пока не ясно. Молекулы противоположной симметрии для нее яд.
Если бы живое существо оказалось в условиях, когда вся пища была бы составлена из молекул противоположной симметрии, не отвечающей дисимметрии этого организма, то оно погибло бы от голода. В неживом веществе правых и левых молекул поровну. Дисимметрия - единственное свойство, благодаря которому мы можем отличить вещество биогенного происхождения от неживого вещества. Мы не можем ответить на вопрос, что такое жизнь, но имеем способ отличить живое от неживого. Таким образом, асимметрию можно рассматривать как разграничительную линию между живой и неживой природой. Для неживой материи характерно преобладание симметрии, при переходе от неживой к живой материи уже на микроуровне преобладает асимметрия. В живой природе асимметрию можно увидеть всюду. Очень удачно это подметил в романе "Жизнь и судьба" В. Гроссман: "В большом миллионе русских деревенских изб, нет и не может быть двух неразличимо схожих. Все живое - неповторимо.
Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте. На принципе симметрии основан метод аналогий, предполагающий отыскание общих свойств в различных объектах. На основе аналогий создаются физические модели различных объектов и явлений. Аналогии между процессами позволяют описывать их общими уравнениями.
Глава 2. Симметрия растений
Изображения на плоскости многих предметов окружающего нас мира имеют ось симметрии или центр симметрии. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.


Среди цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают характерным свойством: цветок можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Минимальный угол, на который нужно повернуть цветок вокруг оси симметрии, чтобы он совместился с самим собой, называется элементарным углом поворота оси. Этот угол для различных цветов не одинаков. Для ириса он равен 120є, для колокольчика – 72є, для нарцисса – 60є . Поворотную ось можно характеризовать и с помощью другой величины, называемой порядком оси и показывающей, сколько раз произойдет совмещение при 

повороте на 360є. Те же цветы ириса, колокольчика и нарцисса обладают осями третьего, пятого и шестого порядков соответственно.
Особенно часто среди цветов встречается симметрия пятого порядка. Это такие полевые цветы как колокольчик, незабудка, зверобой, лапчатка гусиная и др.; цветы плодовых деревьев – вишня, яблоня, груша, мандарин и др., цветы плодово-ягодных растений – земляника, ежевика, малина, шиповник; садовые цветы – настурция, флокс и др.


В пространстве существуют тела, обладающие винтовой симметрией, т. е. совмещающиеся со своим первоначальным положением после поворота на угол вокруг оси, дополненного сдвигом вдоль той же оси.
Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Это интересное ботаническое явление носит название филлотаксиса, что буквально означает строение листа. Другим проявлением филлотаксиса оказывается устройство соцветия подсолнечника или чешуи еловой шишки, в которой чешуйки располагаются в виде спиралей и винтовых линий. Такое расположение особенно четко видно у ананаса, имеющего более или менее шестиугольные ячейки, которые образуют ряды, идущие в различных направлениях.


Глава 3. Симметрия животных
Внимательное наблюдение обнаруживает, что основу красоты многих форм, созданных природой, составляет симметрия, точнее, все её виды – от простейших до самых сложных. Симметрия в строение животных – почти общее явление, хотя почти всегда встречаются исключения из общего правила.
Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Строение тела многих многоклеточных организмов отражает определённые формы симметрии, такие как радиальную (лучевая) или билатеральную (двусторонняя), которые являются основными типами симметрии. Кстати, склонность к регенерации (восстановление) зависит от типа симметрии животного.


В биологии о радиальной симметрии идёт речь, когда через трёхмерное существо проходят две или более плоскости симметрии. Эти плоскости пересекаются в прямой. Если животное будет вращаться вокруг этой оси на определённый градус, то оно будет отображаться само на себе. В двухмерной проекции радиальная симметрия может сохраняться, если ось симметрии направлена перпендикулярно к проекционной плоскости. Иными словами, сохранение радиальной симметрии зависит от угла наблюдения.
При радиальной или лучистой симметрии тело имеет форму короткого или длинного цилиндра либо сосуда с центральной осью, от которого отходят в радиальном порядке части тела. Среди них встречается так называемая пентасимметрия, базирующаяся на пяти плоскостях симметрии.
Радиальная симметрия характерна для многих стрекающих, а также для большинства иглокожих, кишечнополостных. Взрослые формы иглокожих приближаются к радиальной симметрии, в то время как их личинки билатерально симметричны.
Лучевую симметрию мы также видим у медуз, кораллов, актиний, морских звёзд. Если вращать их вокруг собственной оси, они несколько раз «совместятся сами с собой». Если отрезать у морской звезды любое из пяти щупалец, оно сумеет восстановить всю звезду. От радиальной симметрии различаются двулучевая радиальная симметрия (две плоскости симметрии, к примеру, гребневики), а также билатеральная симметрия (одна плоскость симметрии, к примеру, двусторонне-симметричные).
При билатеральной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны – брюшная и спинная – друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих. Например, черви, членистоногие, позвоночные. У большинства многоклеточных (у человека в том числе) другой тип симметрии – двусторонняя. Левая половина их тела — это как бы «отражённая в зеркале правая». Этот принцип, однако, не относится к отдельным внутренним органам, что демонстрирует, например, расположение печени или сердца у человека. Плоский червь планария имеет двустороннюю симметрию. Если разрезать его вдоль оси тела или поперёк, из обеих половинок вырастут новые черви. Если же измельчить планарию как-нибудь иначе — скорее всего ничего не выйдет.
Можно сказать также, что каждое животное (будь то насекомое, рыба или птица) состоит из двух энантиоморфов – правой и левой половин. Энантиоморфы – пара зеркально асимметричных объектов (фигур), являющихся зеркальным изображением один другого (например, пара перчаток). Иными словами – это объект и его зазеркальный двойник при условии, что сам объект зеркально асимметричен.
Сферическая симметрия имеет место у радиолярий и солнечников, тело которых сферической формы, а его части распределены вокруг центра сферы и отходят от неё. У таких организмов нет ни передней, ни задней, ни боковых частей тела, любая плоскость, проведённая через центр, делит животное на одинаковые половинки.
Губки и пластинчатые не проявляют симметрию.
Глава 4. Человек - существо симметричное
Не станем пока разбираться, существует ли на самом деле абсолютно симметричный человек. У каждого, разумеется, обнаружится родинка, прядь волос или какая-нибудь другая деталь, нарушающая внешнюю симметрию. Левый глаз никогда не бывает в точности таким, как правый, да и уголки рта находятся на разной высоте, во всяком случае, у большинства людей. И всё же это лишь мелкие несоответствия. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы! НО! Здесь стоит остановиться. Если бы наши руки и в самом деле были совершенно одинаковы, мы могли бы в любой момент поменять их. Было бы возможно, скажем, путем трансплантации пересадить левую ладонь на правую руку, или, проще, левая перчатка подходила бы тогда к правой руке, но на самом деле это не так. Каждому известно, что сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Многие художники обращали пристальное внимание на симметрию и пропорции человеческого тела, во всяком случае, до тех пор, пока ими руководило желание в своих произведениях как можно точнее следовать природе.
Известны каноны пропорций, составленные Альбрехтом Дюрером и Леонардо да Винчи. Согласно этим канонам, человеческое тело не только симметрично, но и пропорционально. Леонардо открыл, что тело вписывается в круг и в квадрат. Дюрер занимался поисками единой меры, которая находилась бы в определенном соотношении с длиной туловища или ноги (такой мерой он считал длину руки до локтя). В современных школах живописи в качестве единой меры чаще всего принимается размер головы по вертикали. С известным допущением можно считать, что длина туловища превосходит размер головы в восемь раз. На первый взгляд это кажется странным. Но нельзя забывать, что большинство высоких людей отличаются удлинённым черепом и, наоборот, редко можно встретить низкорослого толстяка с головой удлинённой формы. Размеру головы пропорциональна не только длина туловища, но и размеры других частей тела. По этому принципу построены все люди, оттого-то мы, в общем, похожи друг на друга. Однако наши пропорции согласуются лишь приблизительно, а потому люди лишь похожи, но не одинаковы. Во всяком случае, все мы симметричны! К тому же некоторые художники в своих произведениях особенно подчёркивают эту симметрию. И в одежде человек тоже, как правило, старается поддерживать впечатление симметричности: правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например, расчесывая волосы на косой пробор — слева или справа или делая асимметричную стрижку. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или, надев кольцо на безымянный палец только одной руки. Лишь на одной стороне груди носятся ордена и значки (чаще на левой). Полная безукоризненная симметрия выглядела бы нестерпимо скучно. Именно небольшие отклонения от неё и придают характерные, индивидуальные черты.И вместе с тем порой человек старается подчеркнуть, усилить различие между левым и правым. В средние века мужчины одно время щеголяли в панталонах со штанинами разных цветов (например, одной красной, а другой черной или белой). В не столь отдалённые дни были популярны джинсы с яркими заплатами или цветными разводами. Но подобная мода всегда недолговечна. Лишь тактичные, скромные отклонения от симметрии остаются на долгие времена.
Заключение
С симметрией мы встречаемся везде ~ в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.
Еще одним интересным проявлением симметрии являются биологические ритмы (биоритмы), циклические колебания биологических процессов и их характеристик (сокращения сердца, дыхание, колебания интенсивности деления клеток, обмена веществ, двигательной активности, численности растений и животных), зачастую связанные с приспособлением организмов к геофизическим циклам. Исследованием биоритмов занимается особая наука - хронобиология. Помимо симметрии, существует также понятие ассиметрии. Симметрия лежит в основе вещей и явлений, выражая нечто общее, свойственное разным объектам, тогда как асимметрия связана с индивидуальным воплощением этого общего в конкретном объекте.
Литература
1.Урманцев Ю. А. “Симметрия природы и природа симметрии”.
Москва, Мысль, 1974г..
2. А.П. Бондырев « Под небом Сарапулки»
2. http://www.worldnatures.ru
3. http://otherreferats
4. http://ru.wikipedia.org
infourok.ru
Симметрия вокруг нас - HintFox
Трудно найти человека, который не имел бы какого-либо представления о симметрии. В обычной «нематематической» жизни нам уже не раз приходилось говорить о симметрии. Только при этом, наверное, мы чаще использовали слова «симметричный», «симметрично расположенный». С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придает гармоничность, законченность.
В настоящее время учёные расширяют свои учения о симметрии. Добавляются новые обширные разделы, такие как цветная симметрия, симметрия многомерных пространств и др. Свои новые результаты они излагают в монографиях. Значит, выбранная нами тема актуальна.
Слово «симметрия» греческое, оно означает «соразмерность, пропорциональность, одинаковость в расположении частей». Его широко используют все без исключения направления современной науки. Об этой закономерности задумывались многие великие люди. Например, Л. Н. Толстой говорил: “Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия понятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?”. Действительно симметричность приятна глазу. Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, – всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии.
§1. Симметрия в буквах и словах.
Буквы А, М, Т, Ш, П имеют вертикальную ось симметрии, В, З, К, С, Э, В, Е – горизонтальную. А буквы Ж, Н, О, Ф, Х имеют по две оси симметрии. Рассмотрим примеры со всеми известными буквами «И» и «Ф». Что касается буквы «И», то у нее есть так называемая поворотная симметрия. Если повернуть букву «И» на 180( вокруг оси, перпендикулярной к плоскости буквы и проходящей через ее центр, то буква совместится сама с собой. Иными словами, буква «И» симметрична относительно поворота на 180(. Заметим, что поворотной симметрией обладает также буква «Ф». Данные буквы обладают осью симметрии 2-го порядка. Симметрию можно увидеть и в словах: казак, шалаш. Есть и целые фразы с таким свойством (если не учитывать пробелы между словами): “Искать такси”, “Аргентина манит негра”, “Ценит негра аргентинец”, “Леша на палке клапана шел”. Такие слова называются палиндромами. Оказывается, симметрия используется не только в математике, но и в русском языке.
§2. Симметрия в Природе.
«Нам нравится смотреть на проявление симметрии в природе, на идеально симметричные сферы планет и солнца, на симметричные кристаллы, на снежинки, цветы, которые почти симметричны».
Р. Фейнман
«Симметрия» - такая тема, о которой можно говорить и высоким слогом поэзии, и лаконичным языком математики. Приведём слова поэта Валерия Брюсова из произведения «Сонет к форме», которые как нельзя лучше характеризуют всеобщность симметрии: «Есть тонкие властительные связи» Можно сказать, что симметрия властвует и в природе, и в искусстве, и в науке, и в других областях человеческой деятельности.
Можно любоваться листьями и цветами, понаблюдать за бабочками на лугу, присмотреться к снежинкам на окнах, узорам на коврах, причудливой резьбе на храмах и соборах; вглядеться в изумительную красоту памятников архитектуры прошедших эпох или просто обратить внимание на современные здания, машины, привычные предметы нашего быта и увидеть во всём этом проявление законов симметрии.
О симметрии написаны интересные книги, во многих из которых подчёркивается, что симметрия не просто встречается в окружающем нас мире, она «буквально пронизывает» его, соединяя по-своему живое и неживое в этом мире.
Представляем результаты нашего исследования.
2. 1. Рассмотрим симметрию в природе и начнём с науки Ботаники.
Ботаника – наука о растениях. Наше исследование было направлено на выявление примеров симметрии в растениях, то есть мы занимались проблемой поиска закономерностей внешнего строения растений.
Посмотрим на изящное создание Природы – кленовый лист. Кленовый лист симметричен. Если перегнуть его по среднему вертикальному стебельку-прожилке, то получившиеся части листа совпадут друг с другом. И перед нами две половинки – правая и левая! Можно провести опыт и с зеркалом; отражение в зеркале дополнит половину кленового листа до целого. Кленовый лист обладает зеркальной симметрией, и, если его нарисовать на листке бумаги, то полученная плоская фигура будет иметь ось симметрии.
Если присмотреться повнимательнее к прожилкам на левой и правой половинках кленового листа, то можно заметить некоторую разницу между ними. Поэтому говорят, что симметрия кленового листа не является математически точной, или математически безукоризненной. Но эти отклонения столь малы, что не вносят беспорядка в расположение частей и воспринимаются нами как симметричные объекты живой природы.
Дальнейшие наши поиски были сосредоточены на центральной симметрии. Она наиболее характерна для цветов и плодов растений. Центральная симметрия характерна для различных плодов, но мы остановились на ягодах: голубика, черника, вишня, клюква. Рассмотрим разрез любой из этих ягод. В разрезе она представляет собой окружность, а окружность, как нам известно, имеет центр симметрии.
Центральную симметрию можно наблюдать на изображении следующих цветов: цветок одуванчика, цветок мать-и-мачехи, цветок кувшинки, сердцевина ромашки, а в некоторых случаях центральной симметрией обладает и изображение всего цветка ромашки. Весь цветок ромашки обладает центральной симметрией только в случае четного количества лепестков. В случае же нечетного количества лепестков, вспомните анютины глазки, он обладает только осевой. Для цветов характерна и поворотная симметрия, например: цветок шиповника. Этот цветок можно повернуть вокруг некоторой прямой на угол, равный 360( /5 (или кратный ему), и он совместится сам с собой. Эту прямую называют поворотной осью 5-го порядка. Цветок анютины глазки совместится сам с собой только при повороте на 360(. Это значит, что цветок обладает лишь осью первого порядка.
Если внимательно приглядеться к стеблю растения, то окажется, что и здесь действует закон симметрии. Стебель обладает винтовой осью симметрии. У подсолнечника каждый листок появляется после поворота на 72(. Листья на стебле располагаются по спирали так, чтобы, не мешая друг другу, воспринимать солнечный свет. Сумма двух предыдущих шагов спирали, начиная с вершины, равна величине последующего шага.
Выводы:
1. По нашим наблюдениям, в любом растении можно найти какую-то его часть, обладающую осевой, центральной или винтовой симметрией. Это могут быть листья, цветы, стебли, стволы деревьев, плоды, и более мелкие части, такие как сердцевина цветка, пестик, тычинки и другие.
2. Центральная симметрия наиболее характерна для плодов растений и некоторых цветов.
3. Стебли растений обладают осевой симметрией.
4. Симметрия форм, окраски цветков придаёт им красоту.
2. 2. Животный мир и симметрия.
Рассмотрим, как связаны животный мир и симметрия. Как мы знаем, на плоскости существует два вида симметрии: осевая и центральная. Наше исследование заключалось в поиске примеров этих двух видов симметрии в животном мире. Начнём с осевой симметрии.
Все – и дети, и взрослые – удивляются, разглядывая бабочек. Какие лаборатории есть у Природы, что она творит такие чудеса?! Если бабочка сложит свои крылья, то они совпадут, так как крылышки у неё одинаковые. Но одинаковость эта не простая! Если на тельце бабочки провести вертикальную среднюю линию и поставить вдоль этой прямой линии зеркало. То одна половинка бабочки спрячется за зеркало. Но зато другая - отразится в зеркале и перед нами опять появится такая же бабочка. Половинка бабочки и её отражение в зеркале составили целую бабочку. Поэтому говорят, что бабочка зеркально симметрична.
Если мы нарисуем бабочку на листе бумаги, то особую роль для этой плоской фигуры будет играть вертикальная прямая, проходящая посередине туловища бабочки. По обе стороны от этой прямой на одинаковом расстоянии от неё находятся одинаковые элементы рисунка. В этом случае говорят, что данная плоская фигура симметрична относительно прямой, а прямую, которая разделяет фигуру на правую и левую половины, называют осью симметрии. В раскраске бабочки можно обнаружить небольшие отклонения. Поэтому говорят, что симметрия бабочки не является математически точной. Зеркальная симметрия характерна для всех представителей животного мира
Теперь рассмотрим центральную симметрию. По нашим наблюдениям, центральная симметрия наиболее характерна для животных, ведущих подводный образ жизни. Для этих животных характерна и поворотная симметрия, она служит не только для красоты; она прежде всего связана с приспособлением их к окружающему миру, с их жизнестойкостью.
Рассмотрим винтовую, или спиральную симметрию. Винтовая симметрия есть симметрия относительно комбинации двух преобразований – поворота и переноса вдоль оси поворота, т. е. перемещение вдоль оси винта и вокруг оси винта. Встречаются левые и правые винты. Примерами природных винтов являются: бивень нарвала – левый винт; раковина улитки – правый винт; рога памирского барана – один рог закручен по левой, а другой по правой спирали.
Спиральная симметрия не бывает идеальной, например, раковина моллюсков сужается и расширяется на конце.
2. 3. Горизонтальная зеркальная симметрия в природе.
Зеркальная симметрия насекомых, животных и растений является вертикальной симметрией. Можно ещё много назвать объектов природы, для которых характерна вертикальная зеркальная симметрия. А вот с горизонтальной зеркальной симметрией в природе мы встречаемся редко. Лишь тогда, когда рассматриваем отражение в воде.
Отражение в воде - единственный пример горизонтальной симметрии в природе. Быть может, в этом и состоит тайна его очарования?.
Поверхность озера играет роль зеркала и воспроизводит отражение с геометрической точностью. Поверхность воды есть плоскость симметрии.
2. 4. Симметрия кристаллов.
Посмотрим на другие создания Природы – посмотрим на снежинки. Пожалуй, они являются самым ярким примером красоты форм осевой симметрии. Любая снежинка имеет поворотную ось симметрии и кроме того, каждая снежинка зеркально симметрична. Природные снежинки бывают только шестиугольными или любыми другими плоскими или пространственными образованиями с количеством лучей, кратным трём.
Снежинка – это кристалл замёршей воды. Все твёрдые тела в природе состоят из кристаллов. Каждый кристалл имеет форму многогранника, поэтому говорят, что Природа реализовала многогранники – геометрические фигуры, идеальные объекты – в виде кристаллов. Кристалл каменной соли, например, имеет форму куба.
Мир кристаллов - это особый мир симметрии, с которым связаны великие открытия и в области математики, и в области кристаллографии. В этих высоких научных теориях без специальной подготовки, конечно, не разобраться. Но один удивительный факт можно выразить понятными словами. В большинстве растений характерна ось симметрии 5-го порядка, то, оказывается, в кристаллах возможны только оси симметрии 1,2,3,4, и 6-го порядков!
Выводы:
1)Симметрию живого существа определяет направление его движения. Для живых существ, для которых ведущим направлением является направление движения “вперед”, наиболее характерна осевая симметрия. Так как в этом направлении животные устремляются за пищей и в этом же спасаются от преследователей. А нарушение симметрии привело бы к торможению одной из сторон и превращению поступательного движения в круговое.
2)Центральная симметрия чаще встречается в форме животных, обитающих под водой.
3)В природе встречается горизонтальная и винтовая симметрия.
4)Симметрия форм, окраски насекомых, животных придаёт красоту.
5)Мир кристаллов – это особый вид симметрии.
§3. Симметрия в архитектуре.
Архитектура – удивительная область человеческой деятельности. В ней тесно переплетены и строго уравновешены наука, техника, искусство. Только соразмерное, гармоничное сочетание этих начал делает возводимое человеком сооружение памятником архитектуры. Архитектурный облик здания архитектор создает с помощью строительного материала, образ же его созидается творческим мышлением. Одним из художественных средств, которые он использует, является композиция здания. От неё в первую очередь зависит впечатление, которое оставляет архитектурное сооружение Элементы симметрии можно увидеть в общих планах зданий, архитектуры фасадов, в оформлении внутренних помещений, колоннах, потолках и т. д. В большинстве случаев они обладают осевой симметрией.
Мы провели небольшое исследование в своём селе. Прогуливаясь по нему, рассмотрели 10 административных зданий, определили количество фасадов зданий обладающих осевой симметрией. По результатам построили диаграмму и сделали вывод о том, что большинство фасадов зданий нашего села обладают осевой симметрией, но если фасад здания не обладает осевой симметрией, то, разбив строение на маленькие пристройки, мы обнаружим, что они обладают осевой симметрией.
Выводы:
1. Симметрия широко используется в архитектуре.
2. Использование симметрии в конструкции зданий, симметричных элементов в отделке, а также симметрично расположенные строения создают красоту и гармонию.
3. Прогулявшись по своему селу, мы убедились, что удачных решений может быть очень много, но неизменным остается одно – стремление архитектора к гармонии, а это в той или иной степени связано с симметрией.
§4. Симметрия орнаментов и бордюров.
Искусство создания орнамента и строгие законы математики связаны тонкими, но прочными нитями. Узоры, полученные с помощью переноса, поворота и отражения фигур, являются прекрасными образцами влияния законов симметрии на соединение частей в единое целое. Для названия этих узоров, основанных на построении в определённом порядке составляющих их элементов, используют специальное слово – «орнамент».
В разные времена люди создавали орнаменты для украшения предметов быта, одежды; для декорирования зданий, мостов, улиц и т. д. Орнаменты можно обнаружить и в наскальных рисунках, и в росписях дворцов, и на обоях современных квартир. Различают орнаменты линейные (бордюры) и сетчатые (или плоские). Периодически повторяющийся рисунок на длинной ленте называют бордюром. Любой бордюр обладает переносной симметрией вдоль оси переноса. В простейшем случае симметрия бордюров исчерпывается переносной симметрией. Более сложные бордюры наряду с переносной симметрией обладают зеркальной симметрией или имеют поперечные оси симметрии.
Для построения орнаментов на плоскости используют сетки, поэтому эти орнаменты называют ещё и сетчатыми. В основе любого орнамента на плоскости лежит одна из сеток, состоящих из одинаковых параллелограммов, прямоугольников, ромбов, квадратов, правильных треугольников. Элементарная ячейка орнамента определяется ячейкой сетки: косой, прямоугольной, ромбической, квадратной или гексагональной. При этом внутри одной ячейки основной элемент – мотив орнамента – может встретиться только один раз, несколько раз или не повторится ни разу. Но чем сложнее устроена элементарная ячейка, тем оригинальнее и красивее выглядит орнамент. В таком орнаменте можно найти и поворотную, и переносную, и зеркальную симметрии. Орнамент "Летящие птицы", созданный современным голландским художником Эшером основан на косой решетке. Характерный египетский орнамент основан на квадратной решётке. В принципе любой орнамент можно построить посредством параллельных переносов заполненной определенным рисунком элементарной ячейки. Всего существует 17 типов симметрии орнаментов на плоскости. Орнаментальную симметрию считают наиболее сложной симметрией. «Искусство орнамента содержит в неявном виде наиболее древнюю часть известной нам высшей математики, » - говорил Герман Вейль. Ну, а какая она – это часть, нам предстоит узнать в будущем!
Симметрия позволяет совершенствовать и ускорять процесс создания нового (узоры, орнаменты).
Работа в рамках третьего направления дала возможность применить полученные знания на практике. Мы создали макет «Дачный участок», в котором отразили тему «Симметрия вокруг нас». Дачные домики построены симметрично относительно фонтана, на фонтане и крышах домов мы расположили орнаменты, которые обладают симметрией. На участках растут цветы: анютины глазки, обладающие осевой симметрией и ромашки, обладающие центральной симметрией, т. к. имеют чётное количество лепестков. Здесь же Вы можете увидеть и бабочку, и божью коровку, которые обладают центральной симметрией.
6) Интерпретация (объяснение) результатов. Возможные выводы.
“Принцип симметрии охватывает все новые и новые области”
В. И. Вернадский
Изучая симметрию, мы провели исследование по нескольким направлениям:
• симметрия в буквах;
• симметрия в природе;
• симметрия архитектуре;
• симметрия в орнаментах.
С симметрией мы встречаемся везде – в природе, архитектуре, искусстве. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в математике, биологии, архитектуре, живописи и скульптуре. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии. Существует множество видов симметрии, как в растительном, так и в животном мире, но при всем многообразии живых организмов, принцип симметрии действует всегда, и этот факт еще раз подчеркивает гармоничность нашего мира.
Действительно, симметричные объекты окружают нас буквально со всех сторон, мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Симметрия противостоит хаосу, беспорядку. Получается, что симметрия –
• гармония и красота,
• равновесие,
• устойчивость.
7) Подготовка к презентации исследовательского материала. Написание отчёта.
Для написания отчёта были использованы возможности текстового редактора WORD и табличного редактора EXCEL (подсчёт результатов исследования).
Итоговый материал представлен в виде презентации, выполненной в редакторе POWER POINT. Иллюстративный материал для презентации и буклета был собран в течение 2004-2005 г. в режиме индивидуальной работы в сети ИНТЕРНЕТ на различных сайтах.
Для определения предмета исследования было необходимо «создать» информационное поле изучаемой проблемы: поиск, изучение информации, выделение существенной и несущественной информации, анализ информации.
www.hintfox.com
Осевая симметрия в живой и неживой природе :: SYL.ru
Осевая симметрия и понятие совершенства
Осевая симметрия присуща всем формам в природе и является одним из основополагающих принципов красоты. С древнейших времен человек пытался постигнуть смысл совершенства. Впервые обосновали это понятие художники, философы и математики Древней Греции. Да и само слово "симметрия" было придумано ими. Обозначает оно пропорциональность, гармоничность и тождественность частей целого. Древнегреческий мыслитель Платон утверждал, что прекрасным может быть только тот объект, который симметричен и соразмерен. И действительно, «радуют глаз» те явления и формы, которые имеют пропорциональность и завершенность. Их мы называем правильными.
Осевая симметрия как понятие
Симметрия в мире живых существ проявляется в закономерном расположении одинаковых частей тела относительно центра или оси. Чаще в природе встречается осевая симметрия. Она обуславливает не только общее строение организма, но и возможности его последующего развития. Геометрические формы и пропорции живых существ формирует «осевая симметрия». Определение ее формулируется следующим образом: это свойство объектов совмещаться при различных преобразованиях. Древние считали, что принципом симметричности в наиболее полном объеме обладает сфера. Эту форму они полагали гармоничной и совершенной.
Осевая симметрия в живой природе
Если взглянуть на любое живое существо, сразу бросается в глаза симметричность устройства организма. Человек: две руки, две ноги, два глаза, два уха и так далее. Каждому виду животных присущ характерный окрас. Если в расцветке фигурирует рисунок, то, как правило, он зеркально дублируется с обеих сторон. Это означает, что существует некая линия, по которой животные и люди могут быть визуально поделены на две идентичные половинки, то есть в основе их геометрического устройства лежит осевая симметрия. Любой живой организм природа создает не хаотично и бессмысленно, а согласно общим законам мироустройства, ведь во Вселенной ничто не имеет чисто эстетического, декоративного назначения. Наличие различных форм также обусловлено закономерной необходимостью.
Осевая симметрия в неживой природе
В мире нас повсюду окружают такие явления и предметы, как: тайфун, радуга, капля, листья, цветы и т.д. Их зеркальная, радиальная, центральная, осевая симметрия – очевидны. В значительной степени она обусловлена явлением гравитации. Часто под понятием симметрия понимается регулярность смены каких-либо явлений: день и ночь, зима, весна, лето и осень и так далее. Практически, это свойство существует везде, где наблюдается упорядоченность. Да и сами законы природы – биологические, химические, генетические, астрономические, подчинены общим для нас всех принципам симметрии, поскольку имеют завидную системность. Таким образом, сбалансированность, тождественность как принцип имеет всеобщий масштаб. Осевая симметрия в природе – это один из «краеугольных» законов, на котором базируется мироздание в целом.
www.syl.ru
Симметрия вокруг нас - Литература
Муниципальное образовательное учреждение
СОШ №2
Симметрия вокруг нас
Выполнили: ученики 11 «А» класса
Трофимов Андрей
Накаряков Вячеслав
Проверила: учитель математики
Красильникова Евдокия Васильевна
Пермский край. Г.Оса, 2008 г.
Содержание
Введение 3
Симметрия 4
Виды симметрии 4
Осевая симметрия 4
Центральная симметрия. 5
Трансляционная симметрия 6
Поворот 6
Параллельный перенос. 7
Скользящая симметрия 8
Симметрия относительно плоскости 8
Зеркальная симметрия 9
Симметрия фигур. Распределение по классам симметрий 10
Симметрия неограниченных фигур. 13
Симметрия в природе 13
Симметрии в мире насекомых, рыб, птиц, животных 16
Симметрия в неживой природе 17
Симметрия в искусстве, архитектуре, музыке, литературе. 19
Симметрия в Физике 26
Непрерывные преобразования 26
Дискретные преобразования 28
Симметрия и законы сохранения 30
Симметрия в геометрических преобразованиях графиков функций. 31
Симметрия в геометрических преобразовании графиков функций. 34
Заключение 37
Литература 38
Введение
Симметрия…как таинственна эта вещь, а задумывались ли вы когда-нибудь: «а почему так?» Интересно!
В нашей повседневной жизни мы зачастую сталкиваемся с таким прекрасным природным явлением как «симметрия».
В школьном курсе такой раздел математики как «Симметрия» представлен односторонне.
В нем представлена лишь математическая составляющая свойств симметрии, а об их общекультурном аспекте упоминается вскользь.
Данная робота «Симметрия вокруг нас» направлена на интеграцию знаний, формирование общекультурной компетентности, создание представлений о математика как науке, возникшей из потребностей человеческой практики и развивающейся из неё, а также и собственных внутренних закономерностей. Ведущий подход, который был использован в работе – показать на обширном материале от античных времен до наших дней пути взаимодействия и взаимообогащения двух великих сфер человеческой культуры – науки и искусства, расширить представления о сферах применения математики, показать, что фундаментальные закономерности математики являются формообразующими в архитектуре, в музыке, живописи и т. Д.
Надеемся, что работа окажется полезной для учеников, которые будут поступать в вузы, и учителей, работающих в классах – как общеобразовательных, так и математических..
Симметрия
Термин «cимме́три́я» — (др.-греч. συμμετρία) по гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей».


Математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX веке. В наиболее простой трактовке известного немецкого математика Германа Вейля (1855-1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали.
Мы будем называть симметрией фигуры любое преобразование, переводящее фигуру в себя, т.е. обеспечивающее ее самосовмещение.
Перечислим виды симметрии.
Виды симметрии
Осевая симметрия
Преобразование, при котором каждая точка A фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точу А, при этом отрезок AA´  l , называется осевой симметрией.
l , называется осевой симметрией.

Если точка А лежит на оси l, то она симметрична самой себе, т.е. A совпадает с A´.
В частности, если при преобразовании симметрии относительно оси l,
фигура F переходит сама в себя, то она называется симметричной относительно оси l, а ось l называется ее осью симметрии. 
Центральная симметрия.
Преобразования, переводящее каждую точку A фигуры или тела в точку A´, симметричную ей относительно центра O, называется преобразованием центральной симметрии или просто центральной симметрией.

Точка O называется центром симметрии и является неподвижной. Других неподвижных точек это преобразование не имеет. Если при преобразовании центральной симметрии относительно центра О фигура F преобразуется в себя, то она называется симметричной относительно центра O.при этом центр O называется центром симметрии фигуры F. Примерами фигур, обладающих центром симметрии, являются параллелограмм, окружность и т.д.

Знакомые понятия поворота и параллельного переноса используются при определении так называемой трансляционной симметрии.
Рассмотрим трансляционную симметрию более подробно.
Трансляционная симметрия
Поворот
Преобразование, при котором каждая точка A фигуры или тела поворачивается на один и тот же угол α вокруг заданного центра O, называется вращением или поворотом плоскости. Точка О называется центром вращения, а угол α – углом вращения. Точка O является неподвижной точкой этого преобразования.

Центральная симметрия есть поворот фигуры или тела на 180˚.
Параллельный перенос.
Преобразование при котором каждая точка фигуры или тела перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.
Чтобы задать преобразование параллельного переноса, достаточно задать вектор  .
.

Скользящая симметрия
Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

Все перечисленные преобразования будем называть преобразованиями симметрии. Для преобразований симметрии имеют место следующие свойства:
отрезок переходит в равный ему отрезок;
угол переходит в равный ему угол;
окружность переходит в равную ей окружность;
любой многоугольник переходит в равный ему многоугольник и т.д.
параллельные прямые переходят в параллельные, перпендикулярные в перпендикулярные.
* В стереометрии вводится еще один вид симметрии –
Симметрия относительно плоскости
Рассмотрим произвольную плоскость α в пространстве и такое отображение пространства на себя, при котором каждая точка этой плоскости остается на месте, а точка M, не принадлежащая α переходит в такую точку M´, что плоскость α перпендикулярна отрезку MM´ и проходит через его середину. Это отображение называется симметрией пространства относительно плоскости α.
Математически верное определение
Пусть α - произвольная фиксированная плоскость. Из точки X фигуры опускаем перпендикуляр XA на плоскость α и на его продолжении за точку A откладываем отрезок AX´, равный XA. Точка X´ называется симметричной точке X относительно плоскости α, а преобразование, которое переводит точку X в симметричную ей точку X´, называется преобразованием симметрии относительно плоскости α.
Если точка X лежит в плоскости α, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется симметричной относительно плоскости, а данная плоскость называется плоскостью симметрии этой фигуры.
Зеркальная симметрия
«Что может быть больше похоже на мою руку или моё ухо, чем их собственное отражение в зеркале? И всё же руку, которую я вижу в зеркале «нельзя поставить на место настоящей руки…» (Иммануил Кант)
Все знают, что увидеть зеркальный двойник объекта совсем нетрудно. Достаточно поместить объект перед зеркалом и заглянуть в это зеркало. Обычно считают, что наблюдаемый в зеркале двойник является точной копией самого объекта. В действительности же это совсем не так! Зеркало не просто копирует объект, а меняет местами передние и задние по отношению к зеркалу части объекта. Например, если у вас родинка находится на правой щеке, то у зеркального отображения она будет на левой. Представим вам интересный пример:

Если конус неподвижен, то его легко можно совместить со своим двойником.
Если же конус вращать относительно оси, проходящей через вершину, то направление вращения изменяется при отражении на противоположное. Теперь уже никакими перемещениями и поворотами нельзя совместить объект с зазеркальным двойником.
Симметрия фигур. Распределение по классам симметрий
Фигура обладает симметрией, если существует движение (преобразование не тождественное), переводящее ее в себя.
Например, фигура обладает поворотной симметрией, если она переводится в себя некоторым поворотом.
Одна из самых симметричных фигур конечных размеров - это круг. Каждая прямая, проходящая через его центр, является его осью симметрии, а центр круга является центром поворотной симметрии, причем поворот может быть совершен на любой угол.
Рассмотрим симметрию простейших фигур.
1) Отрезок имеет две оси симметрии и центр симметрии.
2) Треугольник общего вида не имеет никакой симметрии. У равнобедренного (но не равностороннего) треугольника одна ось симметрии - серединный перпендикуляр, проведенный к его основанию.

3) У равностороннего треугольника три оси симметрии, и он имеет поворотную симметрию с углом поворота 120˚.

4) У каждого правильного n-угольника есть n осей симметрии, все они проходят через его центр. Он имеет также поворотную симметрию с углом поворота  .
.
При четном n одни оси симметрии проходят через противоположные вершины, другие - через середины противоположных сторон (и тех и других осей по  ).
).

При нечетном n каждая ось проходит через вершину и середину противоположной стороны.
Центр правильного многоугольника с четным числом сторон является его центром симметрии. У правильного многоугольника с нечетным числом сторон центра симметрии нет.
Давайте рассмотрим более подробно поворотную симметрию.
Предположим, что объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный  (или кратной этой величине, где n = 3;3;4;… ) В этом случае говорят о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.
(или кратной этой величине, где n = 3;3;4;… ) В этом случае говорят о поворотной симметрии, а указанную ось называют поворотной осью n-го порядка.
На рисунке ниже даны примеры простых объектов с поворотными осями разного порядка – от 2-го до 5-го.

Для описания симметрии конкретного конкретного объекта (фигуры, тела) надо указать все поворотные оси и их порядок, а также все плоскости симметрии.
По тому, сколько симметрий имеют фигуры, можно проводить их классификацию.
Распределение по классам симметрии даёт нам новый взгляд на фигуры.
Раньше мы видели только их хаотичное множество, теперь же можно навести в этом множестве порядок.
В математике доказано, что множество симметрий правильного n-угольника состоит из 2n преобразований: n-поворотов и n-осевых симметрий. Класс симметрий обозначаются Dn. Вообще, порядком оси называется число самосовмещений фигуры при повороте вокруг данной оси на 360 градусов. Легко видеть, что порядок оси симметрии правильного шестиугольника равен 6, а о нем самом говорят, что он имеет класс симметрии D6.
Симметрия неограниченных фигур.
Фигура называется ограниченной, если она вся содержится в круге некоторого радиуса с центром в какой-либо своей точке. Если же фигура не лежит ни в каком круге, то она называется неограниченной. Примеры неограниченных фигур: прямая, угол, полоса и т.д.
До сих пор мы рассматривали симметрию ограниченных фигур. При этом переносы не рассматривались. Оказывается, если фигура переходит в себя в результате какого-либо переноса (на ненулевой вектор), то она неограниченна.
О фигуре, которая совмещается с собой при некотором переносе, говорят, что она обладает переносной симметрией. Например, прямая имеет такую симметрию, так как допускает перенос вдоль себя.
Интересны неограниченные фигуры, состоящие из правильно повторяющихся конечных фигур, такие, как квадратная сетка, сетка из прямоугольников, или треугольников, или шестиугольников и других фигур
Реально строить неограниченные фигуры невозможно, но можно мысленно продолжить ограниченную фигуру, "перенося" ее части, как, например, мы легко продолжаем мысленно квадратную сетку. Поэтому мы говорим о симметричности "по переносу" стены, выложенной кафелем, паркета и т.п. Так же понимаем симметричность "по переносу" разнообразных орнаментов.
Симметрия в природе
Совершенно иной характер носит связь математики с красотой в природе, где с помощью математики красота не создается, как в технике и в искусстве, а лишь фиксируется, выражается.
Материал на любом уровне своей организации, будь то минералы, растительный или животный мир, подчиняется строгим законам развития. Сегодня человек с помощью им же созданных точнейших приборов способен проникать в царство бесконечно малых величин, где перед ним раскрываются прекрасные формы.
В основе строения любой живой формы лежит принцип симметрии. Из прямого наблюдения мы можем вывести законы геометрии и почувствовать их несравненное совершенство. Этот порядок, являющийся закономерной необходимостью, поскольку ничто в природе не служит чисто декоративным целям, помогает нам найти общую гармонию, на которой зиждется все мировоздание.
Когда мы хотим нарисовать лист растения или бабочку, то нам приходится учитывать их осевую симметрию. Средняя жилка для листа и туловище для бабочки служит осью симметрии. Центральная симметрия характерна для кристаллов, низших животных и цветов.
Мы видим, что природа проектирует любой живой организм согласно определенной геометрической схеме, причем законы мироздания имеют четкое обоснование.
В своей книге «Этот правый, левый мир» М. Гарднер пишет: «На Земле жизнь зародилась в сферических симметричных формах, а потом стала развиваться по двум главным линиям: образовался мир растений, обладающих симметрией конуса, и мир животных с билатеральной симметрией».
Термин «билатеральная симметрия» часто применяется в биологии. При этом имеется в виду зеркальная симметрия.
Характерная для растений симметрия конуса хорошо видна на примере фактически любого дерева.

Дерево при помощи корневой системы поглощает влагу и пита-тельные вещества из почвы, то есть снизу, а остальные жизненно важные функции выполняются кроной, т. е. наверху. В то же время направления в плоскости, перпендикулярной к вертикали, для де-рева фактически неразличимы; по всем этим направлениям к дере-ву в равной мере поступает воздух, свет, влага.
Дерево имеет вертикальную поворотную ось (ось конуса) и вертикальные плоскости симметрии.
Отметим, что вертикальная ориентация оси конуса, характеризующего симметрию дерева, определяется направлением силы тяжести.
Ярко выраженной симметрией обладают листья, ветви, цветы, плоды.
Зеркальная симметрия характерна для листьев, но встречается и у цветов. Для цветов характерна поворотная симметрия..

Часто поворотная симметрия сочетается с зеркальной или переносной.

В многообразном мире цветов встречаются поворотные оси разных порядков. Однако наиболее распространена поворотная симметрия 5-го порядка. Эта симметрия встречается у многих по-левых цветов.(колокольчик, незабудка, герань, гвоздика, зверобой и лапчатка), у цветов плодовых деревьев (вишня, яблоня, груша, мандарин и др.), у цветов плодово-ягодных растений (земляника, малина, калина, черемуха, рябина, шиповник, боярышник) и др.
В природе существуют тела, обладающие винтовой симметрией, т. е совмещением сосвоим первоначальным положением после поворота на угол φ вокруг оси, дополнительным сдвигом вдоль той же оси.
Если  - рациональное число , то поворотная ось оказывается также осью переноса.
- рациональное число , то поворотная ось оказывается также осью переноса.
Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Это интересное ботаническое явление носит название филлотаксиса (буквально «устроение листа»).
Другим проявлением филлотаксиса оказывается устройство со-цветия подсолнечника или чешуи еловой шишки, в которой че-шуйки располагаются в виде спиралей и винтовых линий. Такое расположение особенно четко видно у ананаса, имеющего более или менее шестиугольные ячейки, которые образуют ряды, идущие в различных направлениях.
Симметрии в мире насекомых, рыб, птиц, животных
Поворотная симметрия 5-го порядка встречается и в животном мире. Примерами могут служить морская звезда и панцирь морского ежа.

Однако в отличие от мира растений поворотная симметрия в животном мире наблюдается редко.
Для насекомых, рыб, птиц, животных характерно несовместимое с поворотной симметрией различие между направлениями «вперед» и «назад».
Направление движения является принципиально выделенным направлением, относительно которого нет симметрии у любого на-секомого, любой птицы или рыбы, любого животного. В этом на-правлении животное устремляется за пищей, в этом же направлении оно спасается от преследователей.
Кроме направления движения симметрию живых существ определяет еще одно направление — направление силы тяжести. Оба направления существенны, они задают плоскость симметрии животного существа.
Билатеральная (зеркальная) симметрия — характерная симметрия всех представителей животного мира.
Эта симметрия хорошо видна у бабочки. Симметрия левого и правого крыла проявляются здесь с почти математической строгостью.

Можно сказать, что каждое животное (а также насекомое, рыба, птица) состоит из двух энантиоморфов — правой и левой половин. Энантиоморфами являются также парные детали, одна из которых попадает в правую, а другая в левую половину тела животного. Так, энантиоморфами являются правое и левое ухо, правый и ле-вый глаз, правый и левый рог и т. д. Отметим, наконец билатеральную симметрию человеческого тела (речь идет о внешнем облике и строении скелета). Эта сим-метрия всегда являлась и является основным источником нашего эстетического восхищения хорошо сложенным человеческим телом.
Симметрия в неживой природе
Еще более ярко и систематически симметричность структуры
материи обнаруживается в неживой природе, именно в кристаллах.
«Кристаллы блещут симметрией», — писал Е. С. Федоров в своем «Курсе кристаллографии».
При слове «кристалл» в воображении рисуется среди драгоценных камней — алмаз: кристальная чистота и прозрачность, чудес-ная, непередаваемая игра света, идеальная правильная форма. Но теперь алмазы уже не только красивый предмет роскоши. Сегодня они служат для обработки наиболее твердых металлов и сплавов. Без них не мыслится современная металлообрабатывающая промышленность.
Оказывается, кристаллы не только алмазы. Обычный сахар и поваренная соль, лед и песок состоят из множества кристалликов. Больше того, основная масса горных пород, образующих земную кору, состоит из кристаллов. Даже обыкновенная глина представляет собой нагромождение мельчайших кристалликов.
Словом, большинство строительных материалов — металлы, камень, песок, глина — кристаллические вещества. Можно сказать, что мы живем в домах, построенных из кристаллов. Не удивительно, что кристаллы являются предметом тщательного изучения.
Кристаллы — это твердые тела, имеющие естественную форму многогранников.
Характерная особенность того или иного вещества состоит в постоянстве углов между соответственными гранями и ребрами для всех образцов кристаллов одного и того же вещества. Что же касается формы граней, то для одного и того же вещества они мо-гут значительно отличаться друг от друга.
Для каждого данного вещества существует своя, присущая только ему одному, идеальная форма его кристалла.
Эта форма обладает свойством симметрии, т. е. свойством кристаллов совмещаться с собой в различных положениях путем поворотов, отражений, параллельных переносов.

Кристалл каждого вещества характеризуется определенным комплексом элементов симметрии — видом (классом) симметрии.

Внутреннее устройство кристалла представляется в виде так называемой пространственной решетки, в одинаковых ячейках ко-торой, имеющих форму параллелепипедов, размещены по законам симметрии одинаковые мельчайшие материальные частицы — мо-лекулы, атомы, ионы или их группы.
Опираясь на эти представления, А В Гадолин в 1867 г. доказал, что всего существует 32 вида симметрии идеальных форм кристалла. Любое кристаллическое вещество, каждый кристалл должны при-надлежать к одному из этих видов симметрии. Эти утверждения представляет закон симметрии, один из законов кристаллографии.
Следующий фундаментальный результат был получен в 1890 г. русским кристаллографом Е. С. Федоровым и одновременно немецким математиком А. Шенфлисом, доказавшими чисто геометрически, что существует 230 типов пространственных решеток. В 1912 г. исследованиями кристаллов при помощи рентгеновских лучей была установлена реальность кристаллической решетки.
Многие, если не все, кристаллы более или менее легко раскалываются по некоторым строго определенным плоскостям. Это явление, называемое спайностью, свидетельствует о том, что механические свойства кристаллов анизотропны, т. е не одинаковы по разным направлениям. Но кристаллы анизотропны и в отношении многих других физических свойств. Свет, например, в определенных кристаллах распространяется по различным направлениям с различной скоростью. При нагревании кристалл расширяется по различным направлениям различно. Это же можно сказать о теплопроводности, электропроводности и т.д.
Анизотропность физических свойств так же, как и сама правильность формы кристаллов, тесно связана с их решетчатым строением, т. е. в конечном счете, определяется симметрией их структуры.
Каждая снежинка — это маленький кристалл замерзшей воды Форма снежинок может быть очень разнообразной, но все они обладают симметрией — поворотной симметрией 6-го порядка, и зеркальной симметрией.

Кроме симметрии в природе часто встречается зеркальная асимметрия (ее также называют лево-правой асимметрией). Она играет принципиально важную роль в живых организмах. Характерный пример зеркально-асимметричного объекта — винт или спираль.
М. Гарднер писал «В каждой живой клетке на Земле заложены правые спирали нуклеиновой кислоты. Асимметричная спиральная структура — несомненно, основа жизни».
Некоторые примеры природных винтов: бивень нарвала (левый винт), раковина улитки (правый винт), рога памирского барана энантиоморфы.
Присмотревшись к растениям, можно обнаружить многочисленные проявления винтовой симметрии в расположении листьев на стебле, веток на стволе, в строении шишек, некоторых цветов и т д.
Спирально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спирали расположены семечки в подсолнухах, спиральные движения наблюдаются при росте корней и побегов.
Изучая конструкции раковин, ученые обратили внимание на целесообразность форм и поверхностей раковин: внутренняя по-верхность гладкая, наружная — рифленая. Внутри покоится моллюск. Наружные ребра увеличивают жесткость раковины, и, таким образом, повышается ее прочность. Форма раковины поражает своим совершенством и экономичностью средств, затраченных на ее создание.
У некоторых моллюсков количество частей, формирующих конические раковины,отвечает числам Фибоначчи.
textarchive.ru






