Решение взаимно обратных задач в начальной школе (простые задачи). Какие задачи можно составить используя числовые данные растения
Комбинаторная задача. Простейшие комбинаторные задачи. Комбинаторные задачи: примеры
Преподаватели математики знакомят своих учеников с понятием «комбинаторная задача» еще в пятом классе. Это необходимо для того, чтобы они сумели в дальнейшем работать с более сложными заданиями. Под комбинаторностью задачи можно понимать возможность решить ее с помощью перебора элементов конечного множества.
Главным признаком задач такого порядка является вопрос к ним, который звучит как «Сколько вариантов?» или «Сколькими способами?» Решение комбинаторных задач напрямую зависит от того, понял ли решающий их смысл, сумел ли он правильно представить действие или процесс, которые были описаны в задании.
Как решить комбинаторную задачу?

Важно корректно определить тип всех имеющихся в рассматриваемой задаче соединений, но при этом необходимо произвести проверку относительно того, имеются ли в ней повторы элементов, изменяются ли сами элементы, играет ли большую роль их порядок, а также относительно некоторых других факторов.
Комбинаторная задача может иметь целый ряд ограничений, которые могут быть наложены на соединения. В этом случае понадобится просчитать полностью ее решение и проверить, оказывают ли эти ограничения какое-либо влияние на соединение всех элементов. Если влияние действительно имеется, необходимо проверить, какое именно.
С чего начать?
Для начала необходимо научиться решать простейшие комбинаторные задачи. Овладение простым материалом позволит научиться разбираться в более сложных заданиях. Рекомендуется сначала начать решать задачи с ограничениями, которые не учитываются при рассмотрении более простого варианта.
Также рекомендуется попытаться решать сначала те задачи, в которых нужно рассматривать меньшее количество общих элементов. Таким образом вы сможете понять принцип создания выборок и научиться в дальнейшем самостоятельно создавать их. Если задача, для которой необходимо использовать комбинаторику, состоит из комбинации нескольких более простых, рекомендуется решать ее по частям.
Решение комбинаторных задач
Такие задачи могут показаться простыми в решении, однако комбинаторика достаточно сложна для освоения, некоторые из них не имеют решения уже на протяжении последних сотен лет. Одной из самых известных задач является определение количества магических квадратов специального порядка, когда число n больше 4.

Комбинаторная задача тесно связана с теорией вероятности, которая появилась еще в средневековые времена. Вероятность происхождения того или иного события можно вычислить только с использованием комбинаторики, в данном случае понадобится чередовать все факторы местами, чтобы получить оптимальное решение.
Решение задач
Комбинаторные задачи с решением используются для обучения учеников и студентов работе с данным материалом. Если же говорить в целом, они должны вызвать у человека интерес и желание найти общее решение. Помимо математических расчетов, необходимо применять умственное напряжение и использовать догадку.
В процессе решения поставленных задач ребенок сможет развить у себя математическое воображение и комбинаторные способности, это может серьезно пригодиться ему в дальнейшем. Постепенно уровень сложности решаемых заданий необходимо повышать, чтобы не забывать имеющиеся знания и добавлять к ним новые.
Способ 1. Перебор
Методы решения комбинаторных задач очень сильно отличаются друг от друга, но все они могут быть использованы учеником для получения ответа. Одним из самых простых, но в то же время и самых долгих способов является перебор. При нем необходимо просто перебрать все возможные варианты решения, не составляя каких-либо схем и таблиц.
Как правило, вопрос в такой задаче связан с возможными вариантами происхождения того или иного события, например: какие числа можно составить с помощью цифр 2, 4, 8, 9? Путем перебора всех вариантов составляется ответ, состоящий из возможных комбинаций. Такой способ прекрасно подходит, если количество возможных вариантов сравнительно невелико.
Способ 2. Дерево из вариантов
Некоторые комбинаторные задачи можно решить, только составляя схемы, в которых будет подробно указана информация о каждом элементе. Составление дерева возможных вариантов – еще один способ нахождения ответа. Он подходит для решения не слишком-то сложных задач, в которых имеется дополнительное условие.
Пример такой задачи:
- Какие пятизначные числа можно составить из цифр 0, 1, 7, 8? Для решения понадобится построить дерево из всех возможных комбинаций, при этом имеется дополнительное условие – число не может начинаться с нуля. Таким образом, ответ будет состоять из всех чисел, которые будут начинаться с 1, 7 или 8.
Способ 3. Формирование таблиц
Решение комбинаторных задач можно выполнить и с помощью таблиц. Они схожи с деревом возможных вариантов, поскольку предлагают наглядное решение ситуации. Для нахождения правильного ответа нужно сформировать таблицу, причем она будет зеркальной: горизонтальные и вертикальные условия будут одинаковыми.
Возможные варианты ответов будут получаться на пересечении столбцов и строчек. При этом ответы на пересечении столбца и строки с одинаковыми данными получаться не будут, эти пересечения необходимо особо пометить, чтобы не запутаться при составлении итогового ответа. Этот способ не слишком-то часто выбирается учениками, многие отдают предпочтение дереву с вариантами.
Способ 4. Умножение
Есть еще один способ, с помощью которого можно решить комбинаторные задачи, – правило умножения. Он прекрасно подходит в том случае, когда по условию не нужно перечислять все возможные варианты решения, необходимо просто найти их максимальное количество. Этот метод единственный в своем роде, им пользуются очень часто, когда только начинают решать комбинаторные задачи.
Пример такой задачи может выглядеть следующим образом:
- 6 человек ожидают экзамена в коридоре. Сколько способов можно использовать, чтобы расположить их в общем списке? Для получения ответа необходимо уточнить, сколько их них может быть на первом месте, сколько на втором, на третьем и т. д. Ответом будет число 720.
Комбинаторика и ее виды

Комбинаторная задача не является только лишь школьным материалом, студенты вузов также изучают ее. В науке существует несколько видов комбинаторики, и у каждого из них имеется собственная миссия. Перечислительная комбинаторика должна рассматривать задачи на перечисление и подсчет возможных конфигураций с дополнительными условиями.
Структурная комбинаторика является компонентом вузовской программы, в ней изучаются теории матроидов и графов. Экстремальная комбинаторика также имеет отношение к вузовскому материалу, и здесь имеются свои индивидуальные ограничения. Еще один раздел – теория Рамсея, занимающаяся изучением структур в случайных вариациях элементов. Существует и лингвистическая комбинаторика, которая занимается рассмотрением вопроса о сочетаемости тех или иных элементов между собой.
Методика преподавания комбинаторных задач
Согласно учебным планам, возраст учеников, который рассчитан на первичное знакомство с данным материалом и на решение комбинаторных задач, – 5 класс. Именно там впервые данная тема предлагается на рассмотрение ученикам, они знакомятся с явлением комбинаторности и пытаются решать поставленные перед ними задачи. При этом очень важно, чтобы при постановке комбинаторной задачи использовался метод, когда дети сами занимаются поиском ответов на вопросы.
Кроме всего прочего, после изучения указанной темы будет намного легче вводить понятие факториала и использовать его при решении уравнений, задач и пр. Таким образом, комбинаторность играет важную роль при получении дальнейшего образования.
Комбинаторные задачи: зачем они нужны?
Если вы знаете, что такое комбинаторные задачи, то никаких сложностей с их решением вы испытывать не будете. Методика их решения может пригодиться при необходимости составления расписаний, графиков работы, а также сложных математических вычислений, для выполнения которых не подойдут электронные устройства.
В школах с углубленным изучением математики и информатики комбинаторные задачи изучаются дополнительно, для этого составляются спецкурсы, методические пособия и задачи. Как правило, несколько задач подобного типа могут входить в состав Единого Государственного Экзамена по математике, обычно их «прячут» в части С.
Как решить комбинаторную задачу быстро?
Очень важно суметь разглядеть комбинаторную задачу быстро, поскольку она может иметь завуалированную формулировку, это особенно важно при сдаче ЕГЭ, где каждая минута на счету. Выпишите отдельно информацию, которую вы видите в тексте задачи, на листок, а затем попытайтесь проанализировать ее с точки зрения четырех известных вам способов.
Если вы можете уложить информацию в таблицу или другое образование, пробуйте ее решать. Если классифицировать ее вы не можете, в этом случае лучше всего оставить ее ненадолго и перейти к решению другой задачи, чтобы не терять драгоценное время. Данной ситуации можно избежать, если заранее порешать некоторое количество задач этого типа.
Где найти примеры?
Единственное, что поможет вам научиться решать комбинаторные задачи, – примеры. Их вы можете найти в специальных математических сборниках, которые продаются в магазинах образовательной литературы. Однако там можно найти информацию лишь для студентов вуза, школьникам придется искать задачи дополнительно, как правило, для них задания придумываются остальными учителями.
Преподаватели вузов считают, что студентам необходимо тренироваться и постоянно предлагают им дополнительную учебную литературу. Одним из лучших сборников считается «Методы дискретного анализа в решении комбинаторных задач», написанный в 1977 году и выпускаемый неоднократно ведущими издательствами страны. Именно там можно найти задачи, которые были актуальны на тот момент и остаются актуальными сегодня.
Что делать, если нужно составить комбинаторную задачу?
Чаще всего комбинаторные задачи необходимо составлять преподавателям, которые обязаны научить студентов мыслить нешаблонно. Здесь все будет зависеть от творческого потенциала составителя. Рекомендуется обратить внимание на уже существующие сборники и попробовать составить задачу так, чтобы она сочетала в себе сразу несколько способов ее решения и имела отличные от книжных данные.
Преподаватели вузов в этом плане намного свободнее школьных, они зачастую дают своим студентам задание самим придумать комбинаторные задачи с подробными методами решения и объяснениями. Если вы не относитесь ни к тем, ни к другим, можно попросить помощи у тех, кто действительно разбирается в вопросе, а также нанять частного репетитора. Одного академического часа достаточно для того, чтобы составить несколько подобных задач.
Комбинаторика – наука будущего?
Многие специалисты в области математики и физики считают, что именно комбинаторная задача может стать толчком в развитии всех технических наук. Достаточно лишь нестандартно подойти к решению тех или иных проблем, и тогда можно будет ответить на вопросы, которые уже несколько веков не дают покоя ученым. Некоторые из них всерьез утверждают, что комбинаторика является подспорьем для всех современных наук, особенно космонавтики. Намного проще будет высчитывать траектории полета кораблей с помощью комбинаторных задач, также они позволят определить точное нахождение тех или иных небесных светил.

Реализация нестандартного подхода уже давно началась в азиатских странах, там ученики даже элементарные задачи по умножению, вычитанию, сложению и делению решают, используя комбинаторные методы. На удивление многих европейских ученых, методика действительно работает. Школы Европы пока что только начали перенимать опыт своих коллег. Когда именно комбинаторика станет одним из основных разделов математики, предположить сложно. Сейчас наука изучается ведущими учеными планеты, которые стремятся популяризировать ее.
Решение задач по экологии
 Здравствуйте, уважаемые читатели блога репетитора биологии по Скайпу biorepet-ufa.ru.
Здравствуйте, уважаемые читатели блога репетитора биологии по Скайпу biorepet-ufa.ru.
Почему экология, как раздел общей биологии, занимает особое место в школьном курсе общей биологии. Да сама жизнь, отношение человека к окружающему миру, экологические проблемы, встающие перед человечеством в связи с техническим прогрессом (нередко оборачивающимся путем в никуда) — заставляют относиться к дисциплине экологии с особенным пиететом.
Поэтому не случайно в любых тестах ЕГЭ и ОГЭ по биологии довольно большое место отводится заданиям по экологии.
Как репетитор по биологии много лет наблюдаю такую картину: часть учеников совершенно свободно могут изъясняться на языке экологических терминов, другая часть — наоборот, с трудом воспринимает их.
Самой хорошей базой для подготовки к сдаче экзаменов по биологии, кроме изучения учебников, является Открытый банк заданий ФИПИ, включающий тесты КИМов за все прошлые годы сдачи ЕГЭ и ОГЭ (ГИА) в нашей стране.
Возможно решение некоторых задач по экологии в какой-то степени поможет учащимся лучше разбираться в школьном предмете экологии в целом.
Задача 1. Одна устрица фильтрует до 10 л/ч воды, содержание водорослей в которой составляет 0, 5 г/л. Какое количество энергии в кДж этих водорослей будет усвоено банкой из 1000 устриц, если в 1 г биомассы водорослей содержится 2,5 кДж энергии корма. На процессы жизнедеятельности устрицы тратят до 60% энергии корма.
Если 1 устрица фильтрует 10 л воды в час с содержанием водорослей 0,5 г/л, значит она за час потребит 5 г водорослей. 1000 устриц потребят 5000 г водорослей. Поскольку 1 г биомассы водорослей содержит 2,5 кДж энергии, то в 5000 г будет содержаться 12500 кЖд энергии. Но, поскольку, усвоено устрицами из этого количества энергии будет 60%, а не все 100%, то ответом будет: 12500 х 60: 100 = 7500 кДж.
Задача 2. На территории площадью 100 км2 ежегодно производили частичную рубку леса. На момент организации на этой территории заповедника было отмечено 50 лосей. Через 5 лет численность лосей увеличилась до 650 голов. Еще через 10 количество лосей уменьшилось до 90 и стабилизировалось в последующие годы на уровне 80-110 голов. Определите плотность поголовья лосей: а) на момент времени создания заповедника? б) через 5 лет после создания заповедника? в) после 10 лет создания заповедника?
Что значит «плотность» поголовья? Это количество особей (в данном случае лосей) на 1 км2.а) поскольку на момент времени создания заповедника на 100 км2 обитало 50 штук лосей, то плотность популяции лосей составляла 50 : 100 = 0,5 особи на км2;б) через 5 лет после создания заповедника плотность популяции достигала 650 : 100 = 6,5 особей на км2;в) через 10 лет после стабилизации численности лосей, плотность популяции составила 90 : 100 = 0,9 особи на км2.То есть сначала численность лосей резко возросла, так как территория стала охраняемой и из-за происходящих до этого вырубок леса существовала для лосей обильная кормовая база в виде молодого подроста кустарников и деревьев на бывших вырубках леса. Затем, так как лес больше не вырубали, а не съеденные лосями молодые деревья выросли, произошло снижение кормовой базы для лосей (лоси, хотя и большие, но они не жирафы, чтобы дотягиваться до веток выросших деревьев) и численность их стабилизировалась на определенном уровне (около 1 особи на км2).
Задача 3. Какова плотность популяции сосны обыкновенной в сосняке зеленомошнике если на 4 площадках, площадью 10 на 10 метров каждая, было отмечено соответственно 14,17,12,13 деревьев?Ответ — деревья на гектары.
Для расчета плотности популяции (чего бы там ни было) в среднем на 1 га (площадь 100х100 м2) необходимо иметь репрезентативную (или достаточную для количественной обработки данных) выборку каких-либо площадок меньшего размера.В данной задаче такими площадками являются сотки (1 сотка = 10х10 м2). Если средняя плотность популяции сосны в пересчете на 1 сотку составляет (14+17+12+13):4 = 14 деревьев, а в 1 га находится 100 соток, то в пересчете на 1 га плотность популяции сосны обыкновенной в этом сосняке зеленомошнике составит 14х100 = 1400 деревьев.
Задача 4. Какова плотность популяции дятла пестрого большого, если на площадке размером 400 на 400 метров было зафиксировано 2 заселенных дупла? Ответ — пары на км2 .
Следует понимать так, что «2 заселенных дупла» имеется в виду заселенных парой особей (самцом и самкой). Хотя это не всегда бывает так: гнездо самец неимоверными усилиями выдолбит, а самки ему не достанется.
Определим, сколько искомых площадок площадью 400 м х 400 м (или 160000 м2) содержится в 1 км2. В 1 км2 (1000 м х 1000 м) находится 1000000 м2. 1000000 : 160000 = 6,3 площадки.
Так как на каждой площадке было обнаружено по два заселенных дупла (по две особи в каждом дупле), то всего плотность популяции дятла составит 2 дупла х 6,3 площадок = 12,6 пар особей на км2. (или 25,2 штук дятлов: что-то мне это напомнило задачу по арифметике про два с половиной велосипедиста в ответе).
Задача 5. Охотоведы установили, что на площади 20 км квадратных таежного леса обитало 8 соболей из них 4 самки. Взрослые особи пар не образуют. в среднем за 1 год самка приносит трех детенышей. Смертность детей и взрослых в конце года составляет 10%. Определить численность соболей в конце года, плотность до начала размножения и в конце года, смертность за год, рождаемость за год.
Что может «смущать» в этом задании? Может быть: откуда у самок будут детеныши появляться, если «взрослые особи у соболей пар не образуют»? Но, конечно же, имеется в виду, что не образуют УСТОЙЧИВЫХ пар, длительное время совместно ухаживающих за потомством.
Значит в данном случае просто речь идет о свободно-скрещиваемой популяции соболей.
Если каждая из 4 самок принесет по 3 щенка, то вся популяция соболей на данном участке леса составила бы 20 особей. Так как в среднем 2 особи (10%) в течение года погибнут, то останется к концу года 18 особей.
Итак, как надо оформить ответы: численность соболей в конце года достигнет 18 особей; плотность весной составляла 0,4 особи/км2, а плотность в конце года 0,9 особи/км2; показатель смертности за год – 2 особи; показатель рождаемости за год (несмотря на смертность) равен 12 особям.
Задача 6. Близкородственные виды часто обитают вместе, хотя принято считать, что между ними существует наиболее сильная конкуренция. Почему в этих случаях не происходит вытеснения одним видом другого?
К ответу на этот вопрос следует подойти комплексно, то есть попытаться обосновать все возможные экологические причины, лежащие вообще в основе взаимоотношений особей в сообществах:
1. Очень часто совместно обитающие близкие виды могут занимать разные экологические ниши, что выражается в различиях: а) состава предпочитаемой пищи; б) способах добывания корма; в) «микроместообитаний» в каждой конкретной экологической нише; г) могут быть активны в разное время суток.
2. Ресурс, за который виды соперничают, находится в избытке.
3. Вытеснения может не происходить, если численность конкурентно более сильного вида постоянно ограничивается хищником или третьим конкурентом.
4. Нестабильность внешних условий среды обитания, которые могут поочередно становиться благоприятными то для одного, то для другого вида.
Задача 7. Для каждой предложенной пары организмов подберите ресурс (из приведенных ниже), за который они могут конкурировать: ландыш – сосна, полевая мышь – обыкновенная полевка, волк – лисица, окунь – щука, канюк – сова-неясыть, барсук – лисица, рожь – василек синий, саксаул – верблюжья колючка, шмель – пчела. Ресурсы: нора, нектар, семена пшеницы, вода, зайцы, свет, мелкая плотва, ионы калия, мелкие грызуны.
Отвечая на этот вопрос, следует вообще вспомнить, что имеется в виду под словом «ресурс». Конечно, чаще всего подразумевается пищевой ресурс, но под «ресурсом» можно подразумевать и какую-либо конкретную нишу обитания.
Ландыш и сосна (оба растительные организмы, нуждающиеся с поглощении минеральных веществ из почвы), хотя и образуют в экосистеме различные ярусы, но могут конкурировать за такой пищевой ресурс как ионы калия.
Полевая мышь и обыкновенная полевка — два близкородственных вида отряда грызунов могут обитать на одной территории и конкурировать, например, за семена пшеницы.
Волк и лисица — оба относятся к отряду хищники, в рационе питания которых большую долю составляют бедные – зайцы.
Окунь и щука – хищные рыбы, объектом их конкурентной борьбы может являться мелкая плотва.
Канюк и сова-неясыть — хищные птицы одного ареала обитания — их пищевой ресурс – мелкие грызуны.
Барсук и лисица — эти оба организма нуждаются (в основном для разведения потомства) в таком нишевом экологическом ресурсе как – нора.
Рожь и василек — оба организма тоже растения, как и в первом ответе, но это светолюбивые растения (никогда не будут расти под густым пологом леса), поэтому их конкурентный ресурс — свет.
Саксаул и верблюжья колючка,- обитатели пустынь. Так как эти оба вида растений хотя и являются ксерофитами (приспособленными к жизни при недостатке влаги), все же лимитирующим фактором их развития в аридных зонах (пустыни) будет являться именно вода.
Шмель и пчела – эти два рода перепончатокрылых насекомых нуждаются в сходном источнике питания — нектаре.
Задача 8. В пруду обитает популяция из 15 щук.1 щука в среднем за месяц съедает около 20 карасей. На сколько особей увеличится численность популяции карасей к концу года если щуки съедают примерно 40% их годового прироста.
Поскольку 1 щука за месяц съедает 20 карасиков, то вся популяция щук 15 штук съест за месяц 300 карасиков. А за год щуки съедят 300 х 12 = 3600 штук карасей. По условию задания известно, что это количество карасей составляет 40% от их годового прироста, тогда весь годовой прирост популяции карасей составит 3600 х 100%: 40% = 9000 штук карасей.
Задача 9. В озере обитает популяция плотвы из 400 половозрелых особей. Удельная рождаемость плотвы составляет 50 потомков в год на одну половозрелую самку. Плотва является основным кормом для популяции из 20 щук, которые съедают примерно 60% годового прироста плотвы. Одна щука в среднем съедает около 20 особей плотвы в месяц. Какой половой состав (в %) имеет популяция плотвы?
Подобные задания удобно рассматривать с конца. Так как 1 щука съедает 20 особей плотвы в месяц, то вся популяция щук, состоящая из 20 особей, съест 400 особей плотвы в месяц. Значит за год будет съедено 400 х 12 = 4800 особей плотвы.Известно, что это количество плотвы составляет 60% ее годового прироста. Тогда прирост плотвы за год будет 4800 х 100% : 60%= 8000 особей. Поскольку 1 самка производит 50 потомков (на самом деле икры выметывается во много раз больше, а речь идет об удельной рождаемости или о количестве выживших особей), то 8000 особей плотвы могли появиться на свет от 8000 : 50 = 160 особей самок. Вся популяция плотвы в озере 400 особей или 100%, тогда 160 особей самок составляют 40% от всей популяции (соответственно, самцов тогда будет 60%).
Задача 10. В одном из районов саванн популяция львов состоит из 40 особей. Основной пищей им являются косули. Популяция косуль способна за год восстановить свою численность на 25%. Один лев в среднем в год убивает до 100 косуль, что составляет 4% годового прироста их популяции. Чему будет равна численность популяции косуль через год при условии, что на данную территорию вселится ещё 10 львов? Сможет ли данная популяция сохранить своё существование(нижний предел численности равен 1000 особей), если другие хищники за год будут съедать до 2000 косуль?
Нам известно, что 100 особей косуль составляют 4% годового прироста популяции, тогда весь прирост популяции за год будет в 25 раз больше или 2500 косуль. Дано также по условию задачи, что этот прирост равный 2500 косулям составляет 25% численности популяции.
Значит вся популяция косуль равна 2500 * 4 = 10000 особей. 50 львов (40 аборигенов и 10 пришлых) за год съедят 50 *100 = 5000 косуль, поэтому численность косуль через год (даже без учета восстановления популяции) составит 10000 — 5000 = 5000 косуль. Даже если другие хищники будут съедать еще 2000 косуль, останется 3000 косуль (что больше 1000 особей необходимых для существования популяции), поэтому данная популяция косуль сможет сохранить свое существование.
Задача 11.В XIX веке популяционные экологи разрабатывали множество математических моделей, описывающих динамику численности популяции различных живых существ. Одна из предложенных формул расчёта скорости роста популяции представлена ниже:δN=r⋅N⋅(K−N)/K,где δN — изменение численности популяции за фиксированный период времени;N — численность популяции в начальный момент данного периода;K — ёмкость среды, равная максимально возможной устойчивой численности популяции;r — репродуктивный потенциал, коэффициент, характеризующий скорость воспроизводства, зависит от величины выбранного отрезка времени и характеристик биологического вида;.Примечательно, что данная формула применима в некотором приближении к популяции любого биологического вида.Вам поручено управление заповедником.В рамках программы восстановления популяции редких видов млекопитающих в Ваш заповедник в 2016 году было интродуцировано 50 зубров. Известно, что на территории заповедника может теоретически жить 1000 особей зубра, а репродуктивный потенциал данного вида составляет 1.2 (отрезок времени в данном случае — 1 год). В каком году численность зубра впервые снизится по сравнению с предыдущим?В ответе укажите число в формате ГГГГ
Фактически нам надо определить через сколько лет численность зубров возрастет на 950 особей, то есть достигнет емкости среды в 1000 особей и на следующий год перестанет увеличиваться (и может даже снизиться, по сравнению с предыдущим годом). Сначала найдем какова будет численность популяции через 1 год: δN = 1,2 * 50 * (1000 — 50) : 1000 = 57 особей. Значит, прирост данной популяции зубров за год составляет 7 особей.Учитывая, что репродуктивным потенциалом называют, хотя и очень, очень усредненную, но величину постоянную (так как с увеличением численности популяции, хотя рождаемость будет увеличиваться, но и смертность тоже будет увеличиваться), мы можем определить через сколько лет численность популяции зубров увеличится на 950 экземпляров. 950 : 7 = 135,7 лет (приходится округлить до 136 лет). 2016 + 136 = 2152 год. Значит уже в 2153 году (на следующий год) численность популяции зубра может быть меньше, чем в 2152 году.
Задача 12. Рассчитайте численность и плотность (пар/100 га) популяции вьюрков на острове, при условии, что площадь острова составляет 20 га, и на каждый гектар площади гнездится 5 пар вьюрков. Какова будет плотность популяции при равномерном распределении на острове, площадью 5 га?
Если на 1 га гнездится 5 пар вьюрков, то на острове площадью 20 га будет обитать 5 х 20 = 100 пар вьюрков. Тогда плотность пар на 100 га составит 500 пар (или численность вьюрков будет равна 1000 особей). Плотность популяции вьюрков на острове площадью 5 га составит 25 пар.
Задача 13. Рассчитайте на усыхающем участке леса площадью 1 га плотность популяции короедов, при условии, что на каждом квадратном метре леса встречается 3 дерева, на каждом из которых отмечено в среднем по 5 жуков.
Поскольку на 1 дереве встречается в среднем по 5 жуков, то на 3 деревьях или на 1 м2 площади будет находиться 15 жуков. Значит, на участке леса 1 га (1 га = 100 м х 100 м = 10000 м2) будет находиться 150000 жуков.
Задача 15. При учете плотности популяции крапчатого суслика полигон исследования в 1 га был разбит на 100 квадратов 10×10 м, в каждом из которых подсчитывалось количество гнездовых нор. В итоге были получены следующие данные: 60 площадок не имели нор, 11 – по 1 норе, 18 – по 2 норы, 9 – по 3 норы, 3 – по 4 норы. Определите тип пространственного распределения популяции суслика по отношению дисперсии (S^2) к среднему числу особей на площадке.
Типов пространственного распределения может быть три: 1) когда S^2/m < 1 – распределение будет называться равномерное; 2) S^2/m = 1 – распределение случайное; 3) S^2/m > 1 – групповое распределение. Дисперсия определяется по формуле: S^2 = Сумма (x-m)^2 : n-1,где х — количество особей на конкретной площадке;m – среднее количество особей на площадке;n – число площадок.Таким образом, чтобы найти среднее квадратическое отклонение или дисперсию S^2 нужно расчертить таблицу из 100 строк номеров участков (с 1 по 100) и по каждой строчке вписать х, x-m, (x-m)^2. Затем просуммировать все (x-m)^2, то есть по 100 строкам и эту величину разделить на 100-1=99. А зная дисперсию и m (m в этой задаче равно 0,86) можно оценить тип пространственного распределения.
Задача 16. Численность одной популяции возросла за месяц от 100 до 200 особей, а второй — от 1000 до 1500 особей. У какой популяции коэффициент мгновенного роста больше?
У первой популяции коэффициент роста r за месяц равен 200 : 100 = 2, а у второй популяции r равен 1500 : 1000 = 1,5.
Задача 17. Объяснить различия терминов редуценты и детритофаги как компоненты экосистемы?
Редуце́нты, а также деструкторы или сапротрофы — это почвенные бактерии и грибы, разрушающие отмершие органические остатки живых существ до СО2, Н2О, NН3 и минеральных солей.Детритофаги — это многие почвенные беспозвоночные животные (в основном черви и личинки насекомых) и некоторые наземные животные, питающиеся падалью (грифы, гиены). Да, они тоже «разрушают» органические вещества до неорганических, но лишь частично, так как выделяют и органические экскременты. Поэтому детритофагов в экологии традиционно относят к консументам.Лишь редуценты в биосфере в целом возвращают основное количество минеральных солей в почву и воду, делая их доступными для продуцентов-автотрофов, и таким образом замыкают биотический круговорот. Поэтому экосистемы не могут обходиться без редуцентов (в отличие от консументов, которые, вероятно, отсутствовали в экосистемах в течение первых 2 млрд лет эволюции, когда экосистемы состояли из одних прокариот).
Задача 18. Прирост биомассы популяции щуки в озере за лето составил 10 кг. Сколько солнечной энергии поглощал фитопланктон за месяц, если известно, что пищевой рацион плотвы за лето составлял 1/5 его прироста, а прирост плотвы за этот же период был равен половине рациона щуки. В 1 кг фитопланктона содержится 6*10^2 ккал энергии. Правило 10 %.
Чтобы обеспечить прирост биомассы щуки на 10 кг за лето, щуки должны были съесть 100 кг плотвы (на этом уровне пищевой цепи мы применили правило 10%). Прирост плотвы за лето был равен 50 кг (так как сказано, что прирост плотвы был равен половине рациона щуки). Чтобы обеспечился прирост плотвы 50 кг, мы должны были бы, применив правило 10%, говорить о 500 кг фитопланктона. Но в данном задании нам дается конкретная величина для пересчета от биомассы плотвы к биомассе фитопланктона: сказано, что пищевой рацион плотвы за лето составлял 1/5 от прироста биомассы фитопланктона. Значит мы должны (вопреки правилу 10%) 50 кг х 5 = 250 кг фитопланктона. То есть именно 250 кг фитопланктона и обеспечат прирост плотвы на 50 кг за лето. В 250 кг фитопланктона содержится 600 ккал х 250 = 150000 ккал. Но столько ккал солнечной энергии нужно для фитопланктона на лето (3 месяца). Значит за месяц фитопланктоном будет поглощено 5*10^3 ккал.
Задача 19. Рост популяции тараканов происходил следующим образом: 1 неделя — 100 особей, 4 неделя — 400 особей, 8 неделя — 680 особей, 12 неделя — 900 особей, 16 неделя — 1120 особей, 20 неделя — 5000 особей. Рассчитать скорость роста популяции.
Скорость роста популяции (r) — это её прирост в единицу времени. Здесь единицей времени следует считать неделю. Очевидно, что в этом задании в разное время скорость роста популяции тараканов была разной. Мне не известна формула расчета, которая могла бы подойти в данной случае, но мои «тараканы» мне подсказывают, что следует подсчитать скорость роста популяции для каждой указанной в задании точки во времени и найти среднюю величину. Скорость роста r1 с 1-й по 4-ю неделю была равна 2 (400 — 100 = 300; 300 : 3 = 100; 100 + 100 = 200; 200 в 2 раза больше 100), с 4 недели по 8 r2 = 1.175, с 8 недели по 12-ю r3 = 1,08, с 12 недели по 16 r4 = 1,06 и с 16 недели по 20-ю r5 = 1,87. Средняя скорость роста популяции тараканов составит r = 1,275 особей в неделю.
Задача 20. Популяция растет с r = 0,5 в сутки. Во сколько раз ее численность увеличится за 0,5, 1 и 2 суток.
Скорость роста популяции (r) за сутки равная 0,5 показывает, что за это время численность популяции увеличится на 50% или будет в 1,5 раза больше, чем начальная численность. Например, если было 100 особей, то через сутки станет 100 + 100 * 0,5 = 150 особей. Тогда, за полсуток в нашем примере популяция увеличится на 25 особей и достигнет численности 125 особей. Значит увеличение её за полсуток составит 125:100 = 1,25 раз, за сутки в 1,5 раза и за 2 суток в 2 раза.
Задача 21. Рассчитайте численность и плотность популяции грызунов в лесном массиве, при условии, что площадь леса составляет 10 га, и на каждом участке 50х100 м встречается 20 особей мышей. Какова будет плотность популяции мышей на площади 1 га?
1 гектар (га) это площадь 100 м х 100 м. Если на полгектара (50х100) приходится 20 особей мышей, то плотность популяции их на 1 га составит 40 особей. Значит, на площади лесного массива в 10 га обитает 400 особей мышей.
Задача 22. При первичном учете доля самок в популяции составила 0,64. После изъятия из популяции 50 самок и 10 самцов доля самок составила 0,51. Найти численность популяции.
Обозначим долю самок буквой Х, долю самцов У (значит численность особей в первичной популяции была Х + У, а во вторичной численность популяции стала Х + У — 60). Теперь осталось составить и решить систему двух таких уравнений: 1) 0,64Х + 0,36У = Х + У; 2) 0,51(Х — 50) + 0,49(У — 10) = Х + У — 60. У меня получилось Х = 198, У = 132. Значит численность всей популяции была 330 зверушек.
Задача 23. В городе проживают 100, 150, 300, 500 тыс. человек. Какую площадь должны иметь леса вокруг этого города, чтобы их хватило для обеспечения населения кислородом и для поглощения выделяемого при дыхании углекислого газа, если в солнечный день 1 га леса поглощает 240 кг углекислого газа и выделяет 200 кг кислорода, а 1 человек в сутки при обычных условиях поглощает в среднем 600 г кислорода и выделяет 750 г углекислого газа.
1. Если расчет вести по кислороду, то нам дано, что на одного человека требуется в сутки 0,6 кг кислорода, значит 1 га леса (да и то, если считать, что все дни в году солнечные, а такого не бывает!) обеспечит кислородом 200 кг : 0,6 кг = 333 человека. Значит на 100 тыс. человек потребуется 100 : 333 х 1000 = 300 га леса, на 150 тыс. человек — 450 га леса, на 300 тыс. человек 900 га леса, на 500 тыс. человек 1500 га леса.2. Если расчет вести по углекислому газу, то нам дано, что один человек в сутки выделяет 0,75 кг углекислоты, значит 1 га леса поглотит углекислоты, выделяемой 240 кг : 0,75 кг = 320 людьми. Значит для поглощения углекислоты, выделяемой 100 тыс. людьми требуется примерно 300 га леса, для поглощения углекислоты, выделяемой 150 тыс. людьми потребуется 450 га леса и т.д. Значит, мы получаем, хотя и очень примерные (на самом деле результаты должны быть больше в 3-5 раз, так как не все дни в году солнечные и имеют температуру, оптимальную для фотосинтеза), но одинаковые результаты расчетов и по кислороду, и по углекислоте.
Задача 24. За сутки человек потребляет 500 л кислорода. На каждого человека в настоящее время приходится одно домашнее животное, которое потребляет кислорода в 5 раз больше. На скольких людей и домашних животных хватит воздуха в атмосфере, если не принимать во внимание другие живые организмы?
Для решения такой задачи нужны точные данные по содержанию кислорода в атмосфере Земли. Да и сам вопрос задачи непонятен. «На скольких людей и домашних животных хватит воздуха в атмосфере»? Что имеется в виду? Чтобы прожить этим «несчастным» людям и животным одни сутки? В общем чушь полнейшая!!! Неужели это не ясно составителям такого задания? Я всё же покажу возможный путь рассуждений.Лишь примерно можно рассчитать количество кислорода в атмосфере. Масса атмосферного воздуха 5 х 10 в степени 18 кг. Так как плотность воздуха 1,2 кг на кубический м, то объем атмосферы примерно 4,2 х 10 в степени 18 кубических метров или 4,2 х 10^21 л. Кислорода в воздухе примерно 20%, значит во всей атмосфере его 8,4 х 10^20 л (эта величина очень и очень не точная, так как не во всём объеме атмосферы такая концентрация кислорода). Из условия задачи 1 человек и 5 его животных за сутки потребляют 3000 л кислорода. Значит кислорода атмосферы хватит, чтобы жить одни сутки 8,4 х 10^20 л : 3000 л = 2,8 х 10^17 количеству человек с их животными.Валентин, составители явно хотели спросить что-то другое. Например, если население планеты не будет больше увеличиваться, то на долго ли нам и нашим пятерым домашним животным хватит кислорода (при невероятном условии, что растения вдруг перестанут его выделять при фотосинтезе).
Задача 25. 3.Уровень содержания кислорода в воде является одним из важнейших факторов в жизни рыб. Назовите дополнительные приспособления, которые имеют некоторые виды рыб, позволяющие им обитать в воде при недостатке кислорода.
Есть так называемые лабиринтовые рыбы (хорошо известные любителям аквариумов): петушки, гурами, макроподы, лялиусы. Эти рыбы способны заглатывать воздух, кислород которого постепенно расходуется в их лабиринтовом аппарате, находящемся в черепе. Есть сомы, которые тоже заглатывают воздух, но усвоение кислорода у них происходит в кишечнике. Наконец, есть так называемые двоякодышащие рыбы: они имеют и жабры, и легкие (лепидосирен, протоптерус, неоцерадот, рогозуб).
Задача 26. Для стимулирования роста дуба в высоту совместно с ним выращивают другие породы (так называемый подгон). Какие особенности биологии дуба используются в этом методе? Объясните, какое значение для лесной промышленности имеет такой прием.
Для лесной промышленности (для заготовления промышленной древесины) надо иметь как можно больше стволовой древесины на 1 га площади. Дуб, растущий вне конкуренции, имеет очень широкую крону (огромную массу боковых мало ценных для промышленности ветвей). Подгон мешает развитию у дуба распространяющейся вширь корневой системы (с корневой системой коррелирует развитие кроны) и дубы становятся более высокими. Древесина подгона тоже может использоваться в лесной промышленности.
Задача 27. Плотность зайцев в данном лесном массиве составляет 200 особей на га. За период размножения из одного помета выживает в среднем 2,3 детеныша. В популяции равное количество самцов и самок. Смертность зайцев условно постоянна, в год гибнет 35% особей. Как будет меняться плотность зайцев в течение 3 ближайших лет?
Поскольку сказано, что в данной популяции зайцев количество самцов и самок одинаковое, то условно можно принять, что на 1 га обитает 100 семей («условно», так как на самом деле у зайцев устойчивых семей нет). В год каждая зайчиха может давать 3-4 помета. Если принять в среднем число пометов 3,5 (в данной задаче вообще не сказано какое число пометов следует брать для расчетов), то в год 100 семей зайцев дадут приплод: 2,3 детеныша х 100 х 3,5 = примерно 800 зайчат. Всего плотность популяции через год была бы 1000 особей, но 35% погибнет, значит останется 650 особей. 650 особей или 325 семей дадут на второй год: 2,3 х 325 х 3,5 = примерно 2600 особей, но так как 355 погибнет, то останется примерно 1700 особей. На третий год: 2,3 х 850 х 3,5 = примерно 6800 особей (это астрономическая величина плотности популяции зайцев для 1 га леса), а с учетом гибели плотность популяции зайцев на гектаре леса в течение 3 лет составит 4400 особей (совершенно не реальная величина, может быть у автора задачи зайцы дают приплод 1 раз в год?).
Задача 28. Рассмотрите трех представителей растительного мира: ксерофит (кактус, алоэ), гидрофит (элодея), гигрофит – живущий при повышенной влажности почвы и воздуха (папоротник, монстера). При этом:а) отметьте особенности внешнего строения, характерные для этих растений;б) из курса биологии вспомните, какие особенности внутреннего строения предлагаемых растений связаны с условиями обитания.
а) кактусы (относятся к стеблевым суккулентам) имеют толстый стебель с запасами воды и листья, превращенные в иголки (для защиты от поедания и уменьшения испарения воды). Алоэ (относится к листовым суккулентам) имеет толстые листья с большим запасом воды, листья имеют кутикулу, что уменьшает испарение воды. Гигрофит элодея — покрытосеменное вторичноводное растение, имеет тонкий стебель и мелкие листочки. Гигрофиты имеют крупные листья.
б) У алоэ и кактусов малое количество устьиц, что уменьшает испарение. У элодеи почти полностью отсутствуют корни и механические ткани. У гигрофитов тонкая кутикула, крупные устьица и мало жилок.
Задача 29. Рассмотрите трех представителей животного мира: наземное млекопитающее, птицу, рыбу. При этом:а) отметьте особенности внешнего строения предлагаемых животных, связанные со средой обитания;б) из курса биологии вспомните, какие особенности внутреннего строения этих организмов можно рассматривать как приспособление к определенной среде обитания.
а) Наземные млекопитающие имеют четыре конечности для быстрого перемещения по твердой поверхности, покрыты шерстью. Птицы — обитают в наземно-воздушной среде, передние конечности превращены в крылья, тело покрыто перьями. Рыбы, обитатели водной среды, имеют тело обтекаемой формы с гладкой поверхностью за счет чешуи и слизи (или только слизи), парные и непарные плавники — все это обеспечивает их активное передвижение в воде.
б) Млекопитающие и птицы имеют четырехкамерное сердце, два круга кровообращения, совершенные альвеолярные и губчатые легкие, что обеспечивает высокий обмен веществ и теплокровность. Птицы имеют облегченный скелет, легочные мешки, у самок один яичник, не имеют зубов, что служит приспособление к полету. Рыбы имеют жабры для дыхания в воде, двухкамерное сердце, один круг кровообращения, обмен веществ невысокий, холоднокровные.
Задача 30. Дана пищевая цепь: дуб—-шелкопряд—-поползень——ястреб. На первом трофическом уровне энергетический запас в виде чистой первичной продукции составляет 5*10(4) кДж энергии. На втором и третьем трофическом уровне на прирост биомассы организмы используют по 10% своего пищевого рациона. Рассчитайте, сколько энергии используют на прирост биомассы консументы 3 порядка, если на дыхание они расходуют 60% и с экскрементами выделяют 35% энергии рациона.
Шелкопряду на прирост биомассы достанется 5*10(3) кДж энергии. Поползню — 500 кДж энергии. Про ястреба — консумента третьего порядка, нам известно, что у него непроизводительные затраты составляют не 90% (как у представителей других уровней этой экологической цепочки), а 95% (60% — расходуется на дыхание, 35% — выделяется с фекалиями). Поэтому у него на прирост биомассы будет потрачено 500 кДж — 500 * 95 : 100 = 25 кДж.
Задача 31. Водоросли и инфузории живут вместе в замкнутом сосуде, стоящем на свету. Инфузории потребляют 0,22 моль глюкозы в неделю, водоросли — 0,24 моль глюкозы в неделю. Суммарная недельная продукция глюкозы составляет 0,5 моль. Как изменится содержание кислорода в этом сосуде через неделю?
Из уравнения фотосинтеза имеем: 6СО2 + 6Н2О = С6Н12О6 + 6О2, то есть на 1 моль глюкозы образуется 6 молей кислорода. В задаче сказано, что за неделю в данной замкнутой системе образуется 0,5 молей глюкозы. Значит выделится 3 моля кислорода. На окисление 0,22 + 0,24 = 0,46 молей глюкозы инфузории и водоросли потратят 0,46 * 3: 0,5 = 2,76 молей кислорода. Значит содержание кислорода в системе через неделю повысится на 3 — 2,76 = 0,24 моля кислорода.
Задача 32. Трофическая цепь водной экосистемы представлена схемой: фитопланктон —> зоопланктон —> плотва —> выдра. Определите минимальную площадь(м2) акватории, обеспечивающей суточную жизнедеятельность 10 особей выдры, если суточный прирост одной выдры составляет 54 ккал, чистая первичная продукция фитопланктона — 270 ккал/м2 в сутки.
Для суточного прироста 10 выдрам требуется 540 ккал. Значит, съеденная ими плотва согласно правилу Линдемана должна содержать 5400 ккал. Эта плотва должна потребить 54000 ккал зоопланктона. Зоопланктон должен потребить 540000 ккал фитопланктона. Столько энергии фитопланктона образуется на площади 540000 ккал : 270 ккал = 2000 м2 = 0,2 га.
****************************************************************
У кого есть вопросы к репетитору биологии по Скайпу, по решению задач по экологии — прошу в комментарии.
У меня на блоге вы можете приобрести ответы на все тесты ОБЗ ФИПИ за все годы проведения экзаменов по ЕГЭ и ОГЭ (ГИА).
www.biorepet-ufa.ru
Обзор алгоритмов кластеризации данных / Хабр
В своей дипломной работе я проводил обзор и сравнительный анализ алгоритмов кластеризации данных. Подумал, что уже собранный и проработанный материал может оказаться кому-то интересен и полезен. О том, что такое кластеризация, рассказал sashaeve в статье «Кластеризация: алгоритмы k-means и c-means». Я частично повторю слова Александра, частично дополню. Также в конце этой статьи интересующиеся могут почитать материалы по ссылкам в списке литературы.
Так же я постарался привести сухой «дипломный» стиль изложения к более публицистическому.
Понятие кластеризации
Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны. Главное отличие кластеризации от классификации состоит в том, что перечень групп четко не задан и определяется в процессе работы алгоритма.Применение кластерного анализа в общем виде сводится к следующим этапам:
- Отбор выборки объектов для кластеризации.
- Определение множества переменных, по которым будут оцениваться объекты в выборке. При необходимости – нормализация значений переменных.
- Вычисление значений меры сходства между объектами.
- Применение метода кластерного анализа для создания групп сходных объектов (кластеров).
- Представление результатов анализа.
Меры расстояний
Итак, как же определять «похожесть» объектов? Для начала нужно составить вектор характеристик для каждого объекта — как правило, это набор числовых значений, например, рост-вес человека. Однако существуют также алгоритмы, работающие с качественными (т.н. категорийными) характеристиками.После того, как мы определили вектор характеристик, можно провести нормализацию, чтобы все компоненты давали одинаковый вклад при расчете «расстояния». В процессе нормализации все значения приводятся к некоторому диапазону, например, [-1, -1] или [0, 1].
Наконец, для каждой пары объектов измеряется «расстояние» между ними — степень похожести. Существует множество метрик, вот лишь основные из них:
- Евклидово расстояние Наиболее распространенная функция расстояния. Представляет собой геометрическим расстоянием в многомерном пространстве:
- Квадрат евклидова расстояния Применяется для придания большего веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:
- Расстояние городских кварталов (манхэттенское расстояние) Это расстояние является средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако для этой меры влияние отдельных больших разностей (выбросов) уменьшается (т.к. они не возводятся в квадрат). Формула для расчета манхэттенского расстояния:
- Расстояние Чебышева Это расстояние может оказаться полезным, когда нужно определить два объекта как «различные», если они различаются по какой-либо одной координате. Расстояние Чебышева вычисляется по формуле:
- Степенное расстояние Применяется в случае, когда необходимо увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Степенное расстояние вычисляется по следующей формуле:, где r и p – параметры, определяемые пользователем. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра – r и p — равны двум, то это расстояние совпадает с расстоянием Евклида.
Классификация алгоритмов
Для себя я выделил две основные классификации алгоритмов кластеризации.- Иерархические и плоские. Иерархические алгоритмы (также называемые алгоритмами таксономии) строят не одно разбиение выборки на непересекающиеся кластеры, а систему вложенных разбиений. Т.о. на выходе мы получаем дерево кластеров, корнем которого является вся выборка, а листьями — наиболее мелкие кластера. Плоские алгоритмы строят одно разбиение объектов на кластеры.
- Четкие и нечеткие. Четкие (или непересекающиеся) алгоритмы каждому объекту выборки ставят в соответствие номер кластера, т.е. каждый объект принадлежит только одному кластеру. Нечеткие (или пересекающиеся) алгоритмы каждому объекту ставят в соответствие набор вещественных значений, показывающих степень отношения объекта к кластерам. Т.е. каждый объект относится к каждому кластеру с некоторой вероятностью.
Объединение кластеров
В случае использования иерархических алгоритмов встает вопрос, как объединять между собой кластера, как вычислять «расстояния» между ними. Существует несколько метрик:- Одиночная связь (расстояния ближайшего соседа) В этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Результирующие кластеры имеют тенденцию объединяться в цепочки.
- Полная связь (расстояние наиболее удаленных соседей) В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т.е. наиболее удаленными соседями). Этот метод обычно работает очень хорошо, когда объекты происходят из отдельных групп. Если же кластеры имеют удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.
- Невзвешенное попарное среднее В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты формируют различные группы, однако он работает одинаково хорошо и в случаях протяженных («цепочечного» типа) кластеров.
- Взвешенное попарное среднее Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т.е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому данный метод должен быть использован, когда предполагаются неравные размеры кластеров.
- Невзвешенный центроидный метод В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.
- Взвешенный центроидный метод (медиана) Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учета разницы между размерами кластеров. Поэтому, если имеются или подозреваются значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.
Обзор алгоритмов
Алгоритмы иерархической кластеризации
Среди алгоритмов иерархической кластеризации выделяются два основных типа: восходящие и нисходящие алгоритмы. Нисходящие алгоритмы работают по принципу «сверху-вниз»: в начале все объекты помещаются в один кластер, который затем разбивается на все более мелкие кластеры. Более распространены восходящие алгоритмы, которые в начале работы помещают каждый объект в отдельный кластер, а затем объединяют кластеры во все более крупные, пока все объекты выборки не будут содержаться в одном кластере. Таким образом строится система вложенных разбиений. Результаты таких алгоритмов обычно представляют в виде дерева – дендрограммы. Классический пример такого дерева – классификация животных и растений.Для вычисления расстояний между кластерами чаще все пользуются двумя расстояниями: одиночной связью или полной связью (см. обзор мер расстояний между кластерами).
К недостатку иерархических алгоритмов можно отнести систему полных разбиений, которая может являться излишней в контексте решаемой задачи.
Алгоритмы квадратичной ошибки
Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения:где cj — «центр масс» кластера j (точка со средними значениями характеристик для данного кластера).
Алгоритмы квадратичной ошибки относятся к типу плоских алгоритмов. Самым распространенным алгоритмом этой категории является метод k-средних. Этот алгоритм строит заданное число кластеров, расположенных как можно дальше друг от друга. Работа алгоритма делится на несколько этапов:
- Случайно выбрать k точек, являющихся начальными «центрами масс» кластеров.
- Отнести каждый объект к кластеру с ближайшим «центром масс».
- Пересчитать «центры масс» кластеров согласно их текущему составу.
- Если критерий остановки алгоритма не удовлетворен, вернуться к п. 2.
К недостаткам данного алгоритма можно отнести необходимость задавать количество кластеров для разбиения.
Нечеткие алгоритмы
Наиболее популярным алгоритмом нечеткой кластеризации является алгоритм c-средних (c-means). Он представляет собой модификацию метода k-средних. Шаги работы алгоритма:- Выбрать начальное нечеткое разбиение n объектов на k кластеров путем выбора матрицы принадлежности U размера n x k.
- Используя матрицу U, найти значение критерия нечеткой ошибки:, где ck — «центр масс» нечеткого кластера k:.
- Перегруппировать объекты с целью уменьшения этого значения критерия нечеткой ошибки.
- Возвращаться в п. 2 до тех пор, пока изменения матрицы U не станут незначительными.
Алгоритмы, основанные на теории графов
Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа G=(V, E), вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность вносения различных усовершенствований, основанные на геометрических соображениях. Основными алгоритмам являются алгоритм выделения связных компонент, алгоритм построения минимального покрывающего (остовного) дерева и алгоритм послойной кластеризации.Алгоритм выделения связных компонент В алгоритме выделения связных компонент задается входной параметр R и в графе удаляются все ребра, для которых «расстояния» больше R. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение R, лежащее в диапазон всех «расстояний», при котором граф «развалится» на несколько связных компонент. Полученные компоненты и есть кластеры.Для подбора параметра R обычно строится гистограмма распределений попарных расстояний. В задачах с хорошо выраженной кластерной структурой данных на гистограмме будет два пика – один соответствует внутрикластерным расстояниям, второй – межкластерным расстояния. Параметр R подбирается из зоны минимума между этими пиками. При этом управлять количеством кластеров при помощи порога расстояния довольно затруднительно.
Алгоритм минимального покрывающего дерева Алгоритм минимального покрывающего дерева сначала строит на графе минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом. На рисунке изображено минимальное покрывающее дерево, полученное для девяти объектов.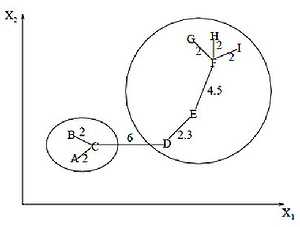
Путём удаления связи, помеченной CD, с длиной равной 6 единицам (ребро с максимальным расстоянием), получаем два кластера: {A, B, C} и {D, E, F, G, H, I}. Второй кластер в дальнейшем может быть разделён ещё на два кластера путём удаления ребра EF, которое имеет длину, равную 4,5 единицам.
Послойная кластеризация Алгоритм послойной кластеризации основан на выделении связных компонент графа на некотором уровне расстояний между объектами (вершинами). Уровень расстояния задается порогом расстояния c. Например, если расстояние между объектами , то .Алгоритм послойной кластеризации формирует последовательность подграфов графа G, которые отражают иерархические связи между кластерами:
,
где Gt = (V, Et) — граф на уровне сt,,сt – t-ый порог расстояния, m – количество уровней иерархии,G0 = (V, o), o – пустое множество ребер графа, получаемое при t0 = 1,Gm = G, то есть граф объектов без ограничений на расстояние (длину ребер графа), поскольку tm = 1.
Посредством изменения порогов расстояния {с0, …, сm}, где 0 = с0 < с1 < …< сm = 1, возможно контролировать глубину иерархии получаемых кластеров. Таким образом, алгоритм послойной кластеризации способен создавать как плоское разбиение данных, так и иерархическое.
Сравнение алгоритмов
Вычислительная сложность алгоритмов O(nkl), где k – число кластеров, l – число итераций| Алгоритм кластеризации | Вычислительная сложность |
| Иерархический | O(n2) |
| k-средних | |
| c-средних | |
| Выделение связных компонент | зависит от алгоритма |
| Минимальное покрывающее дерево | O(n2 log n) |
| Послойная кластеризация | O(max(n, m)), где m < n(n-1)/2 |
| Алгоритм кластеризации | Форма кластеров | Входные данные | Результаты |
| Иерархический | Произвольная | Число кластеров или порог расстояния для усечения иерархии | Бинарное дерево кластеров |
| k-средних | Гиперсфера | Число кластеров | Центры кластеров |
| c-средних | Гиперсфера | Число кластеров, степень нечеткости | Центры кластеров, матрица принадлежности |
| Выделение связных компонент | Произвольная | Порог расстояния R | Древовидная структура кластеров |
| Минимальное покрывающее дерево | Произвольная | Число кластеров или порог расстояния для удаления ребер | Древовидная структура кластеров |
| Послойная кластеризация | Произвольная | Последовательность порогов расстояния | Древовидная структура кластеров с разными уровнями иерархии |
Немного о применении
В своей работе мне нужно было из иерархических структур (деревьев) выделять отдельные области. Т.е. по сути необходимо было разрезать исходное дерево на несколько более мелких деревьев. Поскольку ориентированное дерево – это частный случай графа, то естественным образом подходят алгоритмы, основанными на теории графов.В отличие от полносвязного графа, в ориентированном дереве не все вершины соединены ребрами, при этом общее количество ребер равно n–1, где n – число вершин. Т.е. применительно к узлам дерева, работа алгоритма выделения связных компонент упростится, поскольку удаление любого количества ребер «развалит» дерево на связные компоненты (отдельные деревья). Алгоритм минимального покрывающего дерева в данном случае будет совпадать с алгоритмом выделения связных компонент – путем удаления самых длинных ребер исходное дерево разбивается на несколько деревьев. При этом очевидно, что фаза построения самого минимального покрывающего дерева пропускается.
В случае использования других алгоритмов в них пришлось бы отдельно учитывать наличие связей между объектами, что усложняет алгоритм.
Отдельно хочу сказать, что для достижения наилучшего результата необходимо экспериментировать с выбором мер расстояний, а иногда даже менять алгоритм. Никакого единого решения не существует.
Список литературы
1. Воронцов К.В. Алгоритмы кластеризации и многомерного шкалирования. Курс лекций. МГУ, 2007. 2. Jain A., Murty M., Flynn P. Data Clustering: A Review. // ACM Computing Surveys. 1999. Vol. 31, no. 3. 3. Котов А., Красильников Н. Кластеризация данных. 2006. 3. Мандель И. Д. Кластерный анализ. — М.: Финансы и Статистика, 1988. 4. Прикладная статистика: классификация и снижение размерности. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин — М.: Финансы и статистика, 1989. 5. Информационно-аналитический ресурс, посвященный машинному обучению, распознаванию образов и интеллектуальному анализу данных — www.machinelearning.ru 6. Чубукова И.А. Курс лекций «Data Mining», Интернет-университет информационных технологий — www.intuit.ru/department/database/datamininghabr.com
Комбинаторика. Размещения, перестановки, сочетания | Математика, которая мне нравится
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал однуиз основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при >.
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки ладей
по определению!
Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа
Все сочетания из множества по два — .
.
Свойства чисел {\sf C}_n^k
1. .
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
2. .
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .

.
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данногомножества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?3. Сколько есть шестизначных чисел, делящихся на 5?4. Сколькими способами можно разложить 7 разных монет в три кармана?5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
hijos.ru
Обучение старших дошкольников решению арифметических задач
Библиографическое описание:
Авсюкевич Н. И., Башкатова И. А. Обучение старших дошкольников решению арифметических задач // Вопросы дошкольной педагогики. 2016. №3. С. 103-105. URL https://moluch.ru/th/1/archive/41/1258/ (дата обращения: 17.12.2018).
…За арифметикой, в особенности за арифметическими задачами, всегда признавалась и другая исключительная роль в обучении, а именно развитие сообразительности, смекалки.
А. И. Маркушевич
К моменту поступления в школу дети должны усвоить относительно широкий круг взаимосвязанных знаний о множестве и числе, форме и величине, научиться ориентироваться в пространстве и во времени.
В процессе математического и общего умственного развития детей старшего дошкольного возраста особое внимание уделяется обучению решению и составлению простых арифметических задач. В детском саду проводится подготовительная работа по формированию у детей уверенных навыков вычислений при сложении и вычитании однозначных чисел и быстрых устных вычислений с двузначными числами с целью подготовки их к обучению в начальной школе. Если в школе обучение вычислениям ведется при решении примеров и арифметических задач, то в практике работы дошкольных учреждений принято знакомить детей с арифметическими действиями и простейшими приемами вычисления на основе простых задач, в условии которых отражаются реальные, в основном игровые и бытовые ситуации. В условии задачи указываются связи между данными числами, а также между данными и искомыми. Эти связи и определяют выбор арифметического действия.
Установив эти связи, ребенок довольно легко приходит к пониманию смысла арифметических действий и значения понятий «прибавить», «вычесть», «получится», «останется». Решая задачи, дети овладевают умением находить зависимость величин.
Вместе с тем задачи являются одним из средств развития у детей логического мышления, смекалки, сообразительности. В работе с задачами совершенствуются умения проводить анализ и синтез, обобщать и конкретизировать, раскрывать основное, выделять главное в тексте задачи и отбрасывать несущественное, второстепенное.
Простые задачи, т. е. задачи, решаемые одним действием, принято делить на следующие группы:
К первой группе относятся простые задачи, при решении которых дети усваивают конкретный смысл каждого из арифметических действий, т. е. какое арифметическое действие соответствует той или иной операции над множествами (сложение или вычитание). Эти задачи на нахождение суммы двух чисел и на нахождение остатка.
Воспитатель формирует представления о действиях сложения и вычитания, одновременно знакомит детей со знаками «+», «-», «=». Таким образом, дети постепенно переходят от действий с конкретными множествами к действиям с числами — решают арифметические задачи и знакомятся с записью модели арифметических действий с помощью математических условных знаков.
Уже на 2–3 занятии, где использовался наглядный материал, детям предлагают решать устные текстовые задачи. Для усвоения алгоритма действия полезны упражнения в самостоятельном составлении задач.
4 + 2 = 6
Ко второй группе относятся простые задачи, при решении которых надо осмысливать связь между компонентами и результатами арифметических действий. Это задачи на нахождение неизвестных компонентов:
а) нахождение первого слагаемого по известным сумме и второму слагаемому.
б) нахождение второго слагаемого по известным сумме и первому слагаемому.
в) нахождение уменьшаемого по известным вычитаемому и разности.
г) нахождение вычитаемого по известным уменьшаемому и разности.
Эти задачи помогают закрепить знания о структуре задачи и развивают умение находить соответствующее арифметическое действие. Чтобы дети лучше запоминали числовые данные, используются карточки с цифрами, а в последствии и со знаками.
9–3 = 6
К третьей группе относятся простые задачи, связанные с понятием разности отношений:
а) увеличение числа на несколько единиц.
б) уменьшение числа на несколько единиц.
В этих задачах арифметические действия как бы подсказаны самим условием задачи. Отношение больше на единицу требует от ребенка увеличения, присчитывания, сложения, отношение меньше на единицу — уменьшения, вычитания.
В зависимости от используемого для составления задач наглядного материала они подразделяются на задачи — драматизации и задачи — иллюстрации. Каждая разновидность этих задач обладает своими особенностями и раскрывает перед детьми те или иные стороны, а также способствует развитию умения отбирать для сюжета задачи необходимый жизненный, бытовой, игровой материал, учит логически мыслить.
Особенность задач-драматизаций состоит в том, что содержание их непосредственно отражает жизнь самих детей, т. е. то, что они только что делали или обычно делают. В задачах-драматизациях наиболее наглядно раскрывается их смысл. Дети начинают понимать, что в задаче всегда отражается конкретная жизнь людей.
Умение вдумываться в соответствие содержания задачи реальной жизни способствуют более глубокому познанию жизни, учит детей рассматривать явления в многообразных связях, включая количественные отношения.
Задачи этого вида особенно ценны на первом этапе обучения: дети учатся составлять задачи про самих себя, рассказывать о действиях друг друга, ставить вопрос для решения, поэтому структура задачи на примере задач — драматизаций наиболее доступна детям.
Особое место в системе наглядных пособий занимают задачи — иллюстрации. В этих задачах при помощи игрушек создается простор для разнообразия сюжетов. Эти задачи развивают воображение, стимулируют память и умение самостоятельно придумывать задачи, а следовательно, подводят к решению и составлению устных задач.
Для иллюстрации задач широко применяются картинки. Основные требования к ним простота сюжета, динамизм содержания и ярко выраженные количественные отношения между объектами.
Сделать задачу-картинку может сам воспитатель. Указанные наглядные пособия способствуют усвоению смысла арифметической задачи и ее структуры.
После того как у детей сформированы представления и некоторые понятия об арифметической задаче, об отношениях между числовыми данными, между условием и вопросом задачи, можно переходить к ознакомлению спреобразованием прямых задач вобратные. Это помогает усвоить глубже специфику каждого типа задач. Воспитатель объясняет: любую арифметическую задачу можно преобразовать в новую, если полученное искомое считать одним из данных новой задачи, а одно из данных преобразованной задачи считать искомым.
Примерное задание для обучения детей решению задач в уме.
Воспитатель вывешивает карточки с задачами — картинками, на которых с помощью изображенных предметов и арифметических знаков представлены условия четырех задач.
3 груши-1 груша
2 груши+1 груша
2 ягоды+1 ягода
3ягоды-1 ягода
Выберите из четырех задач-картинок ту, решение которой будет соответствовать заданной величине.
1 задание. Задана величина, равная 3 грушам. Какая задача-картинка подходит? Какое действие в этой задаче нужно выполнить?
2 задание. Задана величина, равная 2 ягодам. Какая задача-картинка подходит? Какое действие в этой задаче нужно выполнить?
3 задание. Воспитатель предлагает найти среди разложенных карточек-картинок те, которые соответствуют ответу.
4 задание. Попробуйте придумать похожие задачи по карточкам-картинкам. Дети придумывают условие задачи, рассказывают, как ее надо решить, и с помощью карточек с цифрами и арифметическими знаками выкладывают ответ в пустой клетке карточки-картинки.
Примерное задание для знакомства детей с задачами на отношение «больше (меньше) на несколько единиц».
Задача: «В Машину чашку с чаем мама положила 2 ложки сахара, а в большую папину чашку — на 1 ложку сахара больше. Сколько ложек сахара положила мама в чашку папы?» О чем говорится в этой задаче? Повторите ее условие. О чем спрашивается в этой задаче? Что надо сделать, чтобы решить задачу? В Машиной чашке 2 ложки сахара — это первое множество. Сколько ложек сахара в папиной чашке — неизвестно. Это второе множество. Но известно, что в папиной чашке на 1 ложку сахара больше, чем в Машиной чашке. Надо определить количество сахара во втором множестве. Сахара в папиной чашке столько же, сколько в первом множестве, и еще на одну ложку больше. С помощью какого действия будем решать задачу? Как ответим на вопрос задачи? Запишите в своих тетрадях решение задачи с помощью цифр и арифметических знаков.
Ознакомление с простыми и обратными задачами повышает познавательную активность, развивает способность логически мыслить.
Основные термины (генерируются автоматически): задача, ребенок, папина чашка, ложок сахара, арифметическая задача, какое действие, действие, какая задача-картинка, наглядный материал, примерное задание.
Похожие статьи
Обучение детей старшего дошкольного возраста решению...
Дошкольникам обычно даются простые задачи, решаемые простым арифметическим действием: задачи на нахождение суммы, остатка. Они должны быть понятны детям по сюжету, изложены доступным языком: «У Саши было 5 марок.
Обучение решению арифметических задач | Статья в журнале...
Решение арифметических задач помогает раскрыть основной смысл арифметических действий, конкретизировать их, связать с определенной жизненной ситуацией. Задачи способствуют усвоению математических понятий, отношений, закономерностей.
Особенности решения арифметических задач умственно...
Педагоги коррекционных школ обучают детей решению простых арифметических задач, развивают понятия временных
На дальнейшее математическое развитие, отмечают психологи, влияет то, в какой степени будет воспринят материал в пропедевтический период.
Использование занимательных дидактических игр, смекалок...
В этом случае, когда занимательная задача доступна ребенку, у него складывается положительное эмоциональное отношение к ней, что и
В процессе решения задач на смекалку обдумывание детьми хода поиска результата предшествует практическим действиям.
Конспект ООД «Формирование элементарных математических...
Материал иоборудование: индивидуальные задания на каждого ребенка, проектор, слайды, две
Задание №4. Игра «Сложи картинку» (картинка из геометрических фигур).
Но сначала проведём пальчиковую гимнастику. Дети, глядя на экран, выполняют заданные действия...
Уголок занимательной математики как средство формирования...
Занимательный игровой материал: игры и задания на трансфигурацию, загадки, головоломки, логические задачи, задачи-шутки, задачи
Обучение математике детей дошкольного возраста немыслимо без использования занимательных игр, задач, развлечений, смекалок, головоломок.
Ситуационная задача как один из современных методических...
В ситуационной задаче — это решение заданий по таксономии целей Б. Блума.
Рассмотрите разнообразие объектов в нашей школе, в том числе мебель, наглядные пособия, спортивный инвентарь, которые
Действия педагога. Глаголы для конструирования задач учителем.
Формирование мышления младшего школьника на уроках...
В ходе обучения алгоритму решения задач «...дети учатся анализировать содержание задач, объясняя, что известно и что неизвестно в задаче, что можно узнать по данному условию и что нужно знать для ответа на вопрос задачи, какие арифметические действия и в какой...
Готовность детей старшего дошкольного возраста к обучению...
В более конкретной трактовке математическая готовность — показатель возможностей выполнения арифметических действий с числами, владения знаковыми системами, основами моделирования, самостоятельность в решении творческих задач и оценке результата [1, с. 136].
moluch.ru
Решение задач на основе свойства деления суммы на число. 3-й класс
Разделы: Начальная школа
Цели урока:
- Совершенствовать умение решать задачи на основе свойства деления суммы на число.
- Создать условия для развития мыслительных операций с помощью специальных упражнений.
- Совершенствовать вычислительные навыки.
Задача урока:
Показать два способа решения задач на основе этого свойства.
Оборудование:
- Учебник “Математика” 3 класс (часть.2) М.И. Моро, М.А.Бантоваи др.
- Карточка достижений.
А |
Б |
В |
Г |
Д |
Е |
|
1 |
О |
Е |
Ж |
Ы |
И |
Я |
2 |
К |
Ц |
Ю |
Ь |
М |
Щ |
3 |
М |
В |
Б |
Й |
Ъ |
Х |
4 |
Р |
З |
У |
Л |
Э |
Н |
- Индивидуальные доски (2 шт.).
- Набор разрезных карточек для парной работы.
Ход урока
1. Организационный момент
На меня все посмотрели, Улыбнулись, тихо сели. Сели правильно, спинку выпрямили, Глаза смотрят и видят. Уши слушают и слышат. Сначала думаю, а потом говорю. Помню, что в классе я не один, Умею слушать мнения других.2. Актуализация знаний.
- Назовите числа от 2 до 20, считая двойками.
- Назовите числа от3 до 30, которые делятся на 3
- Назовите числа, начиная с 4, присчитывая по 4, до 40
- Назовите числа от 50 через 5 до 5.
- Назовите числа, ответы таблицы умножения на 9, начиная с 9.
- Работа с числами
– Посмотрите на числа. Прочитайте.
12, 18, 30, 16.
– Какое число может быть лишним?
(30 – круглое число, 16 – не делится на 3)
49, 7, 64, 56.
(7 – однозначное, 64 – не делится на 7)
Вопрос-помощник: На какие числа делятся все эти числа?(Каждой строчке чисел)
– Используя данные числа, составьте выражения, которые будут подходить к схемам.
– Что для этого надо знать?
(Что они делятся на 3, на 7)
– Прочитайте выражения.
– Что это? (деление суммы на число)
– Как можно найти значение данных выражений?
Есть 2 способа:
- Найти результат суммы и разделить на это число.
- Каждое слагаемое суммы разделить на это число, затем результаты сложить.
– Попробуйте, применив эти способы нахождения деления суммы на число, найти значения данных выражений:
(12+18):3=30 : 3=12:3+18:3 = 4+6 =10
49:7+56:7=7+8=15 105 : 7 =
В первом выражении можно найти, используя оба способа, а во втором выражении – находим результат только 2 способом, 1 способом, при нахождении суммы результат найти не можем, так как делить такие числа ещё не умеем.
– А какие знания могут пригодиться, чтобы найти значение таких выражений?
(Знания о том, как можно разделить сумму на число 2 способами)
– Сегодня каждый из вас попробует себя оценить, используя личную карту достижений. Оцените начало урока, если вы довольны собой, уже включились в работу, то найдите на карте окошко и раскрасьте его. ()
- Работа в паре.
– Перед вами карточки, на которых записаны различные математические выражения.
– Найдите среди них те, которые я прочитаю и выложите перед собой в столбик:
(18 + 36) : 9 (20 + 4) • 3 (48 + 56) : 8 (3 + 7) • 7
– Сравните. Что общего?
(1 действие – сумма)
– Чем отличаются?
(Вторым действием, числами, которые используются)
– Разделите на 2 группы.
– Как назовете эти группы?
(1 гр. – выражения на правило умножения суммы на число, 2 группа – выражения на правило деления суммы на число)
– Как будем находить значение умножения суммы на число? Деления суммы на число?
– Среди карточек найдите оба способа решения данных выражений:
(18 + 36) : 9 18 : 9 + 36 : 9 54 : 9 (20 + 4) • 3 20 • 3 + 4 • 3 24 • 3 (48 + 56) : 8 48 : 8 + 56 : 8 104 : 8 (3 + 7) • 7 3 • 7 + 7 • 7 10 • 7
– Проговаривание.
– Нахождение удобного способа (убирание с доски способов решения, при использовании которых результат найти очень сложно)
– Всегда ли при умножении и делении суммы на число можно использовать оба способа нахождения результата?
3. Постановка цели урока.
– Как вы думаете, а где могут пригодится знания о способах решения деления суммы на число?
(В решении задач, в решении примеров, в нашей жизни)
– Сегодня мы будем решать задачи, используя свойство деления суммы на число.
– Какие цели ставите перед собой?
- Научиться решать задачи, используя данное свойство
- Научиться составлять выражения к задаче
- Узнать какие задачи можно решать двумя способами нахождения деления суммы на число, а какие только одним из способов
– А моя цель, как учителя – помочь применить эти знания в решении задачи понять всегда ли выбранные вами способы решения будут рациональными.
– Для достижения наших целей будем решать задачи.
4. Работа по теме урока.
а) работа по учебнику(с.14 № 1)
– Прочитайте. Это задача?
– Назовите данные и искомое. Выпишите.
9 к, 6 к, 3 д, ? к.
– Какую форму краткой записи предлагаете выбрать для этой задачи?
Расход для 1 девочки |
Количество девочек |
Общий расход |
| Р. ? | 3 д. | 9 к. |
| В. ? | 3 д. | 6 к. |
9 к. – это…(записываем) 6 к. – это…(записываем) 3 д. В какой столбик будем записывать? Почему?
– Знаем ли мы количество конфет “Ромашка”, которые получила 1 девочка? Куда это записать?
– Знаем ли мы количество конфет “Василек”, которые получила одна девочка? Куда поставим?
– Прочитайте вопрос: Сколько всего конфет получила каждая девочка?
– Предположите, глядя на таблицу: могла ли одна из девочек получить только конфеты “Ромашка”?
– Почему?
– Где в краткой записи будет главный вопрос, который требует от насответа на вопрос задачи?
– Как ответить на вопрос задачи?
б) поиск решения от вопроса к данным
(Надо узнать, сколько конфет “Ромашка” и сколько конфет “Василек”получила одна девочка?)
– Как найти сколько конфет “Ромашка” получила одна девочка?
(У нас 9 таких конфет, их разделили поровну между 3 девочками?)
– Как это записать?
- 9 : 3 = 3 (к.)– ромашка для 1 девочки.
- 6 : 3 = 2 (к.) – Василек для 1 девочки.
- 2 + 3 – 5(к.)
– Как предлагаете найти сколько конфет “Василек” получила каждая девочка? Почему?
– Можно ли теперь найти сколько конфет у каждой девочки? Как?
– Сколько конфет получила каждая девочка?
– Можно ли ответить какие конфеты получила каждая девочка?
в) составление записи решения одним выражением
– Попробуйте все записанные действия записать одним выражением7
– С какого действия начинаем собирать?
(с третьего)
3 + 2
– Как в решении получили 3?
9 : 3
– Как получили 2?
6 : 3
– Замените этими частными числа в 3 действии?
– Что у вас получилось?
– Прочитайте, расставьте порядок действий и объясните, что нашли каждым действием.
– Как мы записали решение этой задачи?
(По действиям и одним выражением.)
– Это могут быть разные способы решения задачи? Почему?
(это разные записи одного решения)
– Обратите внимание на выражение, которое мы составили. Что заметили?
(это 2 способ нахождения деления суммы на число)
– Какой же будет 1 способ? Попробуйте найти.
(9 + 6) : 3
– Как вы думаете, подходит ли данный способ решения к этой задаче?
– Объясните, что означает каждое действие.
- 9 + 6 = 15 (к.) – всего у девочек.
- 15 : 3 = 5(к.)
– Сколько действий во 2 способе решения?
– Ответьте, сколько и каких конфет получила каждая девочка?
– Подходит ли этот способ решения?
(да, но мы не можем ответить. какие именно конфеты получит каждая девочка)
г) анализ способов решения задачи
– Сколько способов решения задачи нашли?
– Рассмотрите и сделайте вывод: на основе какого свойства мы смогли 2 способа решения этой задачи?
– Какой из способов для вас более удобный?
– А какой рациональный по вашему мнению? Почему?
– Где мы можем применить эти знания?
– Кто считает, что ему понятны оба способа, отметьте на карточке достижений окошко…()
д) изменение данных задачи
– Попробуйте изменить числовые данные, так, чтобы задача решалась только одним способом?
– О чем обязательно нужно помнить?
(чтобы сумма чисел делилась на 3, в отдельности числа могут и не делиться на 3)
Например: (13 + 11) : 3
(22 + 14) : 3
(8+13) : 3
– Всегда ли в задачах мы можем применить оба способа деления суммы на число?
(нет не всегда, надо обращать внимание на числа, которые используют в задаче)
5. Физминутка
- Гимнастика для глаз
- Игра на внимание найдите и покажите направлением руки слова: огурцы, яблоки, слива, груши.
– Что на ваш взгляд могло бы быть лишним? Почему?
– Что осталось? (груши и яблоки)
– Одним словом – фрукты
– Я вам предлагаю решить задачу, в которой речь пойдет об этих фруктах.
6. Первичное закрепление
а) Работа по задаче (с.14 № 3)
– Прочитайте.
– Сколько кг яблок разложили? (36 кг)
– Сколько кг груш разложили в ящики? (24 кг)
– Что значит разложили в ящики в задаче? (разделили)
– Как раскладывали? (в каждый ящик по 6 кг)
– Ящики были разные? одинаковые? Докажите.
– Как вы думаете, каким свойством будете пользоваться, решая эту задачу?
(Способы нахождения свойства делания суммы на число)
– Предположите, возможно ли применить оба способа? почему?
– Используя схемы на доске, попробуйте найти оба способа решения этой задачи.
б) Самостоятельная работа
1 вариант – 1 способ
2 вариант – 2 способ
2 человека записывают решение на отдельных досках , объясняют решение задачи, остальные проверяют свои решения.
– Какой из способов удобнее?
– Какой рациональный?
– Какое свойство раскрывают эти 2 способа?
– Кому понятны оба способа?
– Отметьте свой успех на карточке достижений. ()
– Хотелось бы вам дома попробовать решить задачу на основе этого свойства?
7. Дача домашнего задания.
Домашняя задача (с.14№ 4)
– Прочитайте. Что значит по 10 книг в каждой?
(т.е. их разложили по 10 книг в одну пачку)
– Кто попробует найти и объяснить 2 способа решения?
– А кто желает остановиться на одном способе?
– Отметьте на карточке достижений окошко()
8. Итог урока
– Вспомните цели, которые ставили перед собой в начале урока?
(Научиться решать задачи 2 способами, используя свойство деления суммы на число)
– Кто считает, что поставленной цели достиг?
– Почему у вас получилось?
Карточка достижений ()
9. Рефлексия
– На карте достижений из букв, которые вы отметили, соберите слово.
– Какое слово у вас получилось?
– Я рада, что у вас на уроке сегодня все получилось, и слово “умницы” тоже.
– Вы – умницы!
– Спасибо за урок!
21.06.2012
xn--i1abbnckbmcl9fb.xn--p1ai
Решение взаимно обратных задач в начальной школе (простые задачи)
Разделы: Начальная школа
ХОД УРОКА
1. Введение.
Перед нашей школой всегда стояла задача построения такой методической системы, которая обеспечивала бы резкое повышение качества знаний при значительной экономии времени, расходуемого на изучение материала. В наше время при все возрастающем потоке информации эта проблема стоит особенно остро.
Еще в 60-е годы Комиссией по определению содержания обучения математике, работающей в АПН СССР, был разработан проект программы по математике. Авторы проекта одним из главных средств ускоренного и сознательного изучения материала в школе считали изменение структуры существующих программ, осуществление более целесообразной группировки вопросов, рациональной группировки вопросов, рациональной последовательности разделов, то есть применение метода противопоставления на уроках математики.
Общепринятая традиционная система обучения математике соблюдает принцип раздельного изучения взаимосвязанных понятий или преобразований. При одновременном изучении взаимосвязанных вопросов в пределах одних и тех же уроков дидактической единицей усвоения становится более крупная единица знаний, чем в случае раздельного изучения их. Переход в обучении к более крупным дидактическим единицам усвоения знаний дает экономию сил и времени.
При изучении задач в курсе математики, как простых, так и сложных, как обычных арифметических, так и типовых оказывается высоко эффективным систематическое применение так называемого метода обратных задач.
Успех обучения решению задач посредством преобразования прямой задачи в обратные задачи объясняется как первопричиной тем, что такой путь заставляет поднимать из сферы подсознания наибольшее разнообразие связей, заключенных в содержании задачи. Это и обеспечивает – на языке дидактики – глубокое и прочное усвоение материала.
На составление и решение обратной задачи уходит несравненно меньше времени, чем на решение новой задачи, так как числовые данные и сюжет остаются прежними; производится здесь лишь логическая операция по переосмыслению ролей чисел; неизвестное в прямой задаче становится известным и наоборот.
Поэтому я взяла для изучения и последующей работы тему “Решение взаимно обратных задач в начальной школе”.
На мой взгляд, самое трудное в начальной школе – научить ребенка грамотно писать, а самое трудное в математике – научить решать задачи.
В процессе работы мне хотелось повысить процент способных детей и уменьшить процент слабых.
Кроме того, в своей работе я стремлюсь к тому, чтобы как можно больший процент детей имел качественный показатель знаний по математике. Далее я опишу, как я этого добиваюсь и каковы результаты молей работы.
Я ознакомилась с мнением различных ученых-методистов (смотреть список литературы) по вопросу классификации задач и решению взаимно обратных задач, как по традиционной, так и по развивающей методике.
Работа со взаимно обратными задачами просматривается у Аритской Н.И., у Свечникова А.А., но у Аритской И.И. нет четкой классификации задач, также, как у Истоминой Н.Б.
Классификация сложных задач в принципе сходна у Эрдниева П.М., Свечникова А.А., Баитовой М.А. но простые задачи Свечников А.А. и Баитова М.А. классифицируют несколько иначе, чем Эрдниев П.М.
За основу я взяла работу над задачами по Эрдниеву П.М., так как на сегодняшний день более четкой классификации задач и методики работы над взаимно обратными задачами я пока не вижу.
Следует отметить существенно важные дидактические достоинства метода обратных задач.
Во время преобразования задачи учащийся выявляет и использует взаимно обратные связи между величинами задачи:
| Прямая задача | Ц. |
К. |
С. |
30 р. |
6 к. |
? р. |
|
| Обратная задача | Ц. |
К. |
С. |
30 р. |
? к. |
180 р. |
Во время преобразования учащийся практически познает связи между действиями. Полезно, например, обратить внимание учащихся на то, что количество действий при решении прямой и обратной задач совпадает (это правило нарушается крайне редко). Кроме того, полезно знать учащимся следующее явление: каждому действию прямой задачи соответствует действие той же ступени в обратной задаче.
Количество комбинаций при составлении обратной задачи ограниченно: оно равно количеству данных в задаче.
Решая обратную задачу, учащийся перестраивает суждения и умозаключения, использованные при решении прямой задачи, преодолевая при этом в мышлении инерцию действий, выполненных при решении прямой задачи.
Решение обратной задачи представляет проверку решения прямой задачи, то есть при этом возникают благоприятные условия для потоков информации по целям обратных связей в мыслительных процессах (систематическое сочетание прямых и обратных задач вырабатывает важное качество личности – чувство самоконтроля).
Учащиеся, составляя обратные задачи, знакомятся со значительно большим разнообразием задач, чем в традиционных задачниках.
При составлении и решении обратных задач выдвигается на первый план анализ и видоизменение математических зависимостей.
Итак, для развития мышления ценны не столько прямые и обратные задачи, взятые вне времени сами по себе, а наиболее важный познавательный элемент заключается в процессе преобразования одной задачи в другую, в сравнении условий, решений, ответов задач, то есть тех “невидимых”, трудно уловимых и трудно изобразимых при логическом анализе элементов мысли, которые связывают решения обеих задач (прямой и обратной).
Однако нельзя забывать, что переходы эти осуществляются во времени: чем меньше интервал времени между противоположными процессами решения взаимно обратных задач, тем быстрее и чаще будут совершаться эти переходы и тем прочнее будут сохраняться в памяти следы этих переходов, то есть тем более глубокими и основательными окажутся осваиваемые знания.
2. Решение простых задач на сложение и вычитание.
Разновидности задач на сложение и вычитание в учебниках математики по традиционной системе как бы перетасованы, что затрудняет возникновение циклических связей мысли.
Задачи на сложение и вычитание целесообразно рассматривать следующими циклами:
- задачи на нахождение суммы и неизвестного слагаемого;
- задачи на нахождение разности, уменьшаемого, вычитаемого;
- задачи на увеличение и уменьшение числа на несколько единиц;
- задачи на разностное сравнение величин.
2.1. Задачи на нахождение суммы и неизвестного слагаемого.
Прямая задача
Катя купила 9 открыток, а Надя 8 открыток. Сколько всего открыток купили девочки?
Краткая запись:
| К. | Н. | Всего |
| 9 от. | 8 от. | ? от. |
Решение: 9 + 8 = 17 (от.)
Ответ: девочки купили 17 открыток.
Дается название вида задачи, вводится таблица видов простых задач.
Обратная задача.
Какие числа были даны в задаче?
Какие числа мы нашли, решая задачу?
Составим новую задачу, для чего неизвестным числом сделаем одно из двух других чисел, например, 9 открыток. Сформулируйте эту задачу.
Катя купила несколько открыток, а Надя 8 открыток. Всего девочки купили 17 открыток. Сколько открыток купила Катя?
Краткая запись:
| К. | Н. | Всего |
| ? от. | 8 от. | 17 от. |
Решение: 17 – 8 = 9 (от.)
Ответ: Катя купила 9 открыток.
Сравните решения задач:
- Обе задачи решаются одним действием.
- Прямая задача – действием сложения, обратная – действием вычитания.
Вводится термин – обратная задача. Определяется вид задачи – нахождение неизвестного слагаемого.
Аналогично вводится вторая обратная задача.
Введение обратных задач не изолированно от прямой, а через нее имеет следующие положительные стороны.
- Достигается ознакомление не только с новой задачей, но и повторение старой.
- Учащиеся усваивают связи между задачами, умозаключения здесь возникают в цикле, во взаимопревращениях друг в друге.
- На следующем этапе мы учимся делать обратные преобразования: дается одна обратная задача, решается, а к ней составляется прямая и другая обратная. Причем, здесь уместно ввести решение задачи уравнением.
Саша купил несколько тетрадей в линейку и 7 тетрадей в клетку. Всего он купил 13 тетрадей. Сколько тетрадей в линейку купил Саша?
- Читаем условие: “Саша купил несколько тетрадей в линейку”. Сколько было – неизвестно, обозначаем “окошечком”.
- Читаем дальше: “и 7 тетрадей в клетку”. Пишем: 7 .
- Всего у него было 13 тетрадей. Пишем: 13 (? 7 13)
- При каком действии получается 13? (? + 7 = 13)
Вместо “окошечка” обозначаем неизвестное число буквой Х. Получается уравнение: Х + 7 = 13
Как решить задачу? (Найти неизвестное слагаемое)
Решение:
Х = 13 – 7
Х = 6
6 + 7 = 13
13 = 13
Эта задача преобразуется в прямую и во вторую обратную.
Совершенно аналогично проводим обучение решению задач на нахождение третьего (четвертого) слагаемого.
В одном ящике 23 кг яблок, во втором – 20 кг, а в третьем 18 кг яблок. Сколько кг яблок в трех ящиках?
Решение: 23 + 20 + 18 = 61 (кг)
Составим обратную задачу:
| 1 ящ. | 2 ящ. | 3 ящ. | Всего |
| ? кг | 20 кг | 18 кг. | 61 кг |
Как найти неизвестное слагаемое? (Из суммы вычесть известное слагаемое)
Как это можно сделать?
1 способ: 61 – (20 + 18) = 23 (кг)
2 способ: (61 – 18) – 20 = 23 (кг)
3 способ: (61 – 20) – 18 = 23 (кг)
Таким образом. При решении задач на нахождение неизвестного слагаемого появляется возможность ознакомления с несколькими способами решения одной и той же задачи.
Сколько еще обратных задач можно составить? (Еще 2 задачи, каждую решить разными способами)
Часто учителя начальных классов выбирают из нескольких способов простейший и им ограничиваются. Но нужно помнить старое дидактическое правило: иногда полезнее одну задачу решить разными способами, чем несколько задач одним и тем же способом.
Естественно, не всегда задачи на уроке мы решаем с преобразованием в обратные. Можно обратную задачу сформулировать и р6ешить устно, сформулировать условие без ее решения, выяснив, какие числа даны, что надо найти и т.д.
2.2. Задачи на нахождение разности, уменьшаемого и вычитаемого.
Прямая задача.
У Веры было 87 рублей. Она купила книгу за 37 рублей. Сколько денег у нее осталось?
Краткая запись:
| Было | Израсходовано | Осталось |
| 87 р. | 37 р. | ? р. |
Решение: 87 – 37 = 50 (р.)
Какие числа были даны в задаче?
Что мы узнали после решения? (50 р. – сколько осталось, разницу между числами)
Определяем вид задачи: нахождение остатка (разности).
Составим обратную задачу, сделав известным число 50 р., а неизвестным то, что было.
У веры было несколько рублей. Она купила книгу за 37 рублей, после этого у нее осталось 50 рублей. Сколько денег было у Веры до покупки?
Эту задачу уместно решить уравнением.
- Сколько денег было у Веры? (Неизвестно – Х)
- Сколько денег она израсходовала?
- Сколько у нее осталось?
- Вопрос задачи?
Запись на доске: Х 37 50
- Чтобы получилось уравнение, нужно эти числа связать знаками. Если человек уплатил (истратил, израсходовал) деньги. То у него их стало больше или меньше?
- Какое действие надо выполнить? (Х – 37 = 50)
- У веры осталось 50 р., да она израсходовала 37 р. Сколько денег у нее было вначале: больше, чем 50, или меньше?
- Почему больше?
- На сколько больше?
- Как узнать, сколько денег было вначале?
Х – 37 = 50
Х = 37 + 50
Х = 87
87 – 37 = 50
50 = 50
Ответ: у Веры было 87 р.
Какой компонент находили?
Каким действием?
Вид задачи: нахождение уменьшаемого.
Сравнение прямой и обратной задач:
Решены одним действием, прямая задача – вычитанием, обратная – сложением.
На последующих уроках решаются задачи в иной последовательности: сначала на нахождение уменьшаемого, затем она преобразуется в задачу на нахождение разности.
Затем мы решаем задачи на нахождение разности, когда вычитаемых несколько.
Прямая задача.
В магазине было 90 коробок конфет. В первый день продали 30 коробок, во второй день – 32 коробки. Сколько коробок конфет продали в третий день?
К этому времени мы изучили следующие свойства:
- прибавление суммы к числу,
- прибавление числа к сумме,
- вычитание суммы из числа,
- вычитание числа из суммы.
Поэтому решение подобных задач разными способами не вызывает особых затруднений у детей.
Краткая запись:
| Было | Израсходовано | Осталось |
| 90 к. | 30 к. и 32 к. | ? р. |
Решение: 1 способ – 90 – (30 + 32) = 28 (к.)
2 способ – (90 – 30) – 32 = 28 (к.)
3 способ – (90 – 32) – 30 = 28 (к.)
Что мы находим в этой задаче?
Составьте обратную задачу на нахождение уменьшаемого.
В магазине было несколько коробок конфет. В первый день продали 30 коробок, во второй – 32 коробки, в третий – оставшиеся 28 коробок. Сколько коробок конфет было в магазине первоначально?
Краткая запись: ? к. 30 к. и 32 к. 28 к.
Решение:
1 способ – (30 + 32) + 28 = 90 (к.)
2 способ – (30 + 28) + 32 = 90 (к.)
3 способ – (32 + 28) + 30 = 90 (к.)
Вслед за задачей на нахождение уменьшаемого вводится задача на нахождение вычитаемого.
Прямая задача.
К обеду в столовой сделали 70 бутербродов. За обедом съели 62 бутерброда. Сколько бутербродов осталось в столовой?
Краткая запись:
| Было | Израсходовано | Осталось |
| 70 б. | 62 б. | ? р. |
Решение: 70 – 62 = 8 (б.)
Изменим краткую запись: 70 б. ? б. 8б.
Составьте по ней обратную задачу. К обеду в столовой сделали 70 бутербродов. После обеда осталось 8 бутербродов. Сколько бутербродов съели за обедом?
Эту задачу удобнее решить уравнением.
Сколько было сделано бутербродов?
Сколько съели?
Сколько осталось? 70 Х 8
Как связать эти три числа?
70 – Х = 8
Х = 70 – 8
Х = 62
70 – 62 = 8
8 = 8
Какой компонент находили?
Определите вид задачи. (Нахождение вычитаемого)
Далее решаются задачи на преобразование задач на нахождение вычитаемого в задачи на нахождение разности.
В конце изучения данной темы необходимо решать изолированные задачи без составления к ним обратных, а иногда решать все три задачи по одной и той же ситуации.
2.3. Задачи на уменьшение и увеличение числа на несколько единиц и задачи на разностное сравнение величин.
К введению понятия разностного сравнения мы находим через прямую задачу на увеличение и уменьшение числа на несколько единиц.
Прямая задача.
Набор цветных карандашей стоит 16 рублей, а набор фломастеров на 12 рублей дороже. Сколько стоит набор фломастеров?
Краткая запись:
| К. | Ф. | |
| 16 р. | на 12 р. дороже | ? р. |
Решение: 16 + 12 = 28 (р.)
Обратная задача: ? р. на 12 р. дороже 28 р.
Набор карандашей стоит несколько рублей. Набор фломастеров на 12 рублей дороже. Он стоит 28 рублей. Сколько стоит набор карандашей?
Производим рассуждения и преобразования: Набор фломастеров на 12 р. дороже, значит, набор карандашей на 12 р. дешевле. Поэтому получаем следующую задачу:
Набор фломастеров стоит 28 руб., набор карандашей на 12 руб. дешевле. Сколько стоит набор карандашей?
Краткая запись:
| К. | Ф. |
| ? р. на 12 р. дешевле | 28 р. |
Решение: 28 – 12 = 16 (р.)
Преобразовываю схему:
на ? р. дешевле
Составьте обратную задачу:
Набор карандашей стоит 16 рублей, а набор фломастеров 28 рублей. На сколько рублей фломастеры дороже карандашей? (На сколько рублей карандаши дешевле фломастеров?)
Решение: 28 – 16 = 12 (р.)
Обязательно сравниваем решение прямой и обратных задач.
На следующих уроках сначала решается задача на разностное сравнение, которая преобразуется в две другие задачи. После этого решаем задачи на сложение и вычитание, выраженные в косвенной форме.
Таким образом, взаимосвязь между задачами на сложение и вычитание укладывается в таблицу (прилагается). В ней обозначены три вида задач на сложение и шесть видов задач на вычитание.
Чтобы обобщить эти задачи и подготовить почву для свернутого решения этих задач, полезно упражнять учащихся по мере изучения материала в составлении нескольких видов задач к одному выражению, например, 15 + 3.
Составьте три задачи, чтобы в них использовались слова:
“больше на…”
“сколько вместе”
“сколько было вначале”
Например:
- В одном ящике было 15 кг яблок, в другом на 3 кг больше. Сколько килограмм яблок во втором ящике?
- В одной коробке 15 кг конфет, в другой – 3 кг. Сколько конфет в двух коробках.
- За обедом съели 3 яблока, после чего в вазе осталось 15 яблок. Сколько яблок было в вазе вначале?
- Эти упражнения содействуют развитию множественных связей (ассоциаций). В данном случае множественная связь имеет следующее строение:
Сложение –
“увеличить на”
“сколько вместе”
“сколько всего”
“сколько было вначале”.
- Составьте четыре задачи на вычитание: 70 – 30.
- У мамы было 70 рублей. Она купила апельсинов на 30 рублей. Сколько денег у ней осталось?
- У мамы было 70 рублей. Она истратила несколько рублей на покупку апельсинов, после чего у нее осталось 30 рублей. Сколько денег мама истратила на апельсины?
- У Коли 70 марок, у Пети на 30 марок меньше. Сколько марок у Пети?
- Зеленая лента 70 см, белая – 30 см. на сколько см зеленая лента длиннее белой?
Здесь формируется следующий пучок ассоциаций:
Вычитание –
“сколько осталось”
“сколько истратили”
“меньше на”
“на сколько меньше (больше)”.
3. Литература.
№ п/п |
Автор |
Издание |
Выходные данные |
1. |
Моро М.И. | Математика, 1 класс Математика, 2 класс Математика, 3 класс |
М., Просвещение, 2001. М., Просвещение, 2002. М., Просвещение, 2003. |
2. |
Аритская И.И. | Математика, 1 класс Математика, 2 класс Математика, 3 класс Математика, 4 класс |
М., Просвещение, 2000. М., Просвещение, 2001. М., Просвещение, 2002. М., Просвещение, 2003. |
3. |
Истомина Н.Б. | Математика, 1 класс Математика, 2 класс Математика, 3 класс Математика, 4 класс |
С., Асс XXI век, 2002. С., Асс XXI век, 2003. С., Асс XXI век, 2004. С., Асс XXI век, 2005. |
4. |
Аритская И.И. | Обучаем по системе Занкова 1 кл., 2 кл., 3 кл. | М., Новая школа, 1993, 1994. |
5. |
Эрдниев П.М. | Взаимно обратные действия в арифметике 2–4 классы | М., Просвещение, 1969. |
6. |
Рудницкая В.Н. | Тематические и итоговые контрольные работы по математике. | М., Дрофа, 1996. |
7. |
Холомкина А.И. | Решение задач на движение | М., Просвещение, 1982. |
8. |
Уткина Н.Г. | Составные задачи в 1 классе | М., Просвещение, 1982. |
9. |
Кондратьева Д.Ф. | Составные задачи небольшой сложности в 1 классе | М., Просвещение, 1982. |
10. |
Гусева Т.В. | Обучение решению простых задач в 1 классе | М., Просвещение, 1982. |
11. |
Свечников А.А. | Решение математических задач в 1 классе | М., Просвещение, 1982. |
12. |
Баитова М.А., Бельтюкова Г.В. | Обучение решению арифметических задач | М., Просвещение, 1984. |
13. |
Шамсутдинова Г.С. | Преемственность в обучении математике | М., Просвещение, 1978. |
14. |
Истомина Н.Б. | Активизация учащихся на уроках математики в нач. классах | М., Просвещение, 1985. |
24.12.2009
xn--i1abbnckbmcl9fb.xn--p1ai
- Ребусы на тему животные и растения с ответами

- Выходу растений на сушу в раннем палеозое предшествовало

- Во сколько ярусов растения растут в экваториальных лесах

- В экваториальных лесах растения растут во сколько ярусов

- Рисунок растения для урока окружающий мир 1 класс

- Проростки растений расходуют на рост много энергии которая

- Отзывы банановая кожура как удобрение для комнатных растений

- Какие растения способны быть хищниками и ловить животных

- Улавливают и преобразуют солнечную энергию в клетках растений
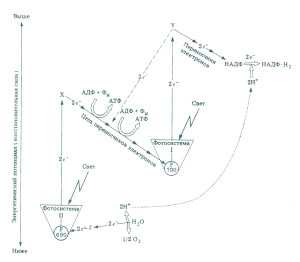
- Использование декоративных и комнатных растений для оформления интерьера

- Никакое растение не производит такое впечатление как баобаб

