Проект на тему: "Математика-это жизнь" ученика 5 класса. Математика в мире растений
Проект по математике "Математика - это жизнь"
МБОУ Лопатинская СОШ
ПРОЕКТ
«Математика - это жизнь»
Авторы:
Хасянова Рафия
ученица 6 класса
Руководитель:
Нескина Ольга Мухтяровна
2015 год
Оглавление
Отзыв о работе.
2. Введение (цель, задачи, гипотеза, методы исследования)
3. Теоретическая часть:
Вступление.
Глава I. Из истории возникновения математики.
§ 1. Возникновение арифметики и теории чисел.
§ 2. Античная математика.
§ 3. Страны ислама.
§ 4. Математика средневековья: IV-XV века.
§ 5. Математика на Руси.
§ 6. Искусство счета.
Глава II. Применение математики в окружающей нас жизни.
§ 1. Математика в мире растений.
§ 2. Математика в жизни животных.
§ 3. Математика геометрических тел и фигур.
§ 4. Математика и культура.
§ 5. Математика в живой и неживой природе.
4. Практическая часть
5. Заключение
6. Список использованных источников информации
7. Приложения
Введение
Данная работа относится к разделу проблемно - исследовательскому.
Цель работы: выяснить, что значит математика в жизни людей: является второстепенной наукой или математика – это неотъемлемая часть в жизни человечества.
Задачи работы:
1) рассмотреть взаимосвязь между математикой и жизнью,
2) проанализировать, как жизнь зависит от математики.
Гипотеза: если математика - второстепенная наука, то законы, которые она изучает знать простому человеку совсем не обязательно, то есть эти законы в обыденной жизни никому не нужны.
Практическая значимость: если гипотеза подтверждается, то можно утверждать, что без математики можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.
Методы исследования:
изучение и анализ литературы по данной теме;
подбор задач, подтверждающих связь математики с жизнью;
сбор и анализ общественного мнения.
Теоретическая часть
Вступление.
На уроке математики нам поручили подготовить проект. Работая над проектом, мы долго не могли определиться с его темой. Нам все было интересно. Так, изучив в 5-м классе простые и составные числа, нам стало интересно, а есть ли число, которое больше вселенной? Ведь при этом нужно учитывать тот факт, что каждое следующее число больше предыдущего хотя бы на единицу. Оказалось очень трудным делом найти самое большое число. Такие числа оказалось для нас не только трудно прочитать, но и записать. А как же с такими числами, спросите Вы, можно выполнять арифметические действия? Ну конечно, ответят им многие, ведь современные компьютеры достигли потрясающих скоростей быстродействия. Поэтому некоторым, кажется, что в современном мире все можно просчитать, достаточно только взять компьютер помощнее. Но это не так.
Ведь до сих пор в мире нет признанной всеми системы наименований больших и сверхбольших чисел. А в словарях, кроме центиллиона, нет названий для чисел, имеющих порядок больше 63 (такое число называют вигинтиллионом).
Свою систему наименований для чисел предлагал Архимед. С ее помощью он мог именовать числа вплоть до 1080000000000000000, которое он называл «последним числом».
Изучив это, мы убедились в том, что попытка найти самое большое число приводит нас в тупик, так как к любому числу достаточно всего лишь прибавить единицу, чтобы получить число большее данного.
Из всего этого мы поняли, что человека окружает громадное количество фактов и явлений, которые в силу своей огромности кажутся далекими и недоступными пониманию, но при глубоком изучении становятся близкими, интересными, загадочными.… И тут нас осенило.
Эврика! Все в мире и в жизни тесно связано с математикой! Вот и нашлась прекрасная тема для проекта: «Математика в жизни людей», или «Математика – это жизнь»
Мы специально не ставим никакого знака препинания в конце предложения, так как считаем, что эту фразу можно произнести с разной интонацией: кто–то её произнесет вопросительно, кто–то с восклицанием, а кто–то просто повествовательно.
В своей работе мы попытаемся выяснить, так что же для нас математика? Может быть, это жизнь, а может быть, это просто наука, которая является для нас второстепенной и заниматься ею нужно только ученым?
Своё исследование мы решили начать с изучения истории математики.
Глава I. Из истории возникновения математики.
§ 1. Возникновение арифметики и теории чисел.
Учёные - археологи обнаружили стойбище древних людей. В нём они нашли волчью кость, на которой 30 тысяч лет назад какой - то древний охотник нанёс 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам.
Много тысячелетий прошло с тех пор. Но и сейчас швейцарские крестьяне, отправляя молоко на сыроварню, отмечают число фляг такими, же зарубками. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером, которой отмечают товар. А ещё 200 - 300 лет тому назад так называли куски дерева, на которых зарубками отмечали сумму долга. Бирку с зарубками раскалывали пополам. При расчёте половинки складывались вместе, и это позволяло определить сумму долга без споров и сложных вычислений.
Первыми понятиями математики, с которыми столкнулись люди, были «меньше», «больше», «столько же». Если одно племя меняло рыбу на сделанные другим племенем каменные ножи, достаточно было положить рядом с каждой рыбой один нож, соответствующий величине рыбы, чтобы сделка состоялась.
А вот так выглядело счётное устройство инков, которое состояло из узелков, завязанных на веревках разной длины. Если внимательно приглядеться, то эти узелки чем-то отдаленно напоминают счеты.
Для запоминания результатов счёта использовали зарубки, узелки и т. п.
Были и более экзотичные варианты. Например, такие математические таблицы древних, обнаружены на территории современной Армении.
Одна из древнейших нумераций, дошедших до нас в древних папирусах и рисунках, была – египетская.
Для записи чисел египтяне использовали картинки-иероглифы, означавшие буквально следующее:
- собственно 1. - 10. - 100. - 1 000. - 10 000. - 100 000. - 1 000 000. - 10 000 000.
К примеру, число 2253 на этой картинке было изображено так:
- две тысячи, две сотни, пять десятков и три единицы.
Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта и подчинении его власти Александра Македонского.
Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел. Недаром ведь говорят: «Без названия нет знания».
О том, как появились имена у чисел, учёные узнают, изучая языки разных народов и племён. Ведь, как известно, учёные считают, что сначала названия получили числа 1 и 2.
Когда римляне (в древности они говорили на латыни) придумывали имя числу 1(солюс), они исходили из того, что Солнце на небе одно. А название для числа 2 во многих языках связано с предметами, встречающимися попарно, - крыльями, ушами, руками и т.д.
А есть более экзотичные варианты.
Например, на языке некоторых папуасских племён (о. Новая Гвинея) числа назвали так: 1 - «урапун», 2 - «оказа», 3 - «оказа -урапун», 4 - «оказа - оказа», 5 - «оказа - оказа - урапун», 6 - «оказа - оказа - оказа» и «много», как самое большое число. Правда, интересно! Но тогда как, же считать такими числами расстояния до звезд, размеры галактики, или как этими числами папуасские племена обозначали бы мельчайшие размеры атома?!
§ 2. Античная математика.
Третий век до нашей эры был золотым веком античной математики.
В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию.
В III веке до н. э. в городе Александрия Птолемей I основал Дом Муз и пригласил туда виднейших учёных. Это была первая академии, с богатейшей библиотекой, которая к I веку до н. э. насчитывала 70000 книг.
Но самая громкая слава выпала на долю трёх великих геометров античной математики – это, конечно же, Евклид, Архимед и Апполоний Пергский. Евклид (написал книгу «Начала», авторитет которой был и остается огромным более 2000 лет), Архимед (развил метод вычисления площадей и объёмов геометрических фигур и тел), Аполлоний Пергский (автор исследования сечений геометрических тел).
А такие два достижения греческой математики далеко пережили своих творцов.
1) греки построили и представили миру математику как целостную науку;
2) греки провозгласили, что законы природы постижимы для человеческого разума.
§3. Страны ислама
Математика Востока, в отличие от греческой, всегда носила более практический характер. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика. Преследование греческих учёных-нехристиан в Римской империи V—VI веков вызвало их массовое бегство на восток, в Персию и Индию. При дворе Хосрова I они переводили античных классиков на сирийский язык, а два века спустя появились арабские переводы этих трудов. Так было положено начало ближневосточной математической школе. Большое влияние на неё оказала и индийская математика, также испытавшая сильное древнегреческое влияние. В начале IX века научным центром халифата становится Багдад, где халифы создают «Дом мудрости», в который приглашаются виднейшие учёные всего исламского мира —сабии (потомки вавилонских жрецов-звездопоклонников), тюрки и другие. На западе халифата, в испанской Кордове, сформировался другой научный центр, благодаря которому античные знания стали понемногу возвращаться в Европу. Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, были задачи о расчёте лунного календаря, об определении киблы — точного направления на Мекку.
В целом, эпоха исламской цивилизации в математических науках может быть охарактеризована не как эпоха поиска новых знаний, но — как эпоха передачи и улучшения знаний, полученных от греческих математиков.
§4. Средневековье, IV - XV века
В это время мы можем отметить расцвет математики как науки.
В конце XII века на базе нескольких монастырских школ был создан Парижский университет. Возникают Оксфорд и Кембридж в Британии.
Первым крупным математиком средневековья стал Леонардо Пизанский, известный под прозвищем Фибоначчи.
§5. Математика у русского народа
Интерес к науке на Руси появился рано. Сохранились сведения о школах при Владимире Святославовиче и Ярославе Мудром (XI век).
Русский народ создал свою собственную систему мер:
1 миля = 7 верстам ( 7,47 км)
1 верста = 500 саженям ( 1,07 км)
1 сажень = 3 аршинам = 7 футам ( 2,13 м)
1 аршин = 16 вершкам = 28 дюймам ( 71,12 см)
1 фут = 12 дюймам (30,48 см)
1 дюйм = 10 линиям ( 2,54 см)
1 линия = 10 точкам ( 2,54 мм).
Интересно, что на Руси когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см, или о богатырях говорили «Богатырь, косая сажень в плечах», т.е. у такого человека по диагонали от мизинца левой руки до пятки правой ноги почти 2 метра 13 сантиметров.
§ 6. Искусство счета.
Изучив этот материал, мы поняли, что искусство счета развивалось с развитием человечества. На ранних ступенях развития общества люди почти не умели считать. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Это был еще не счет, а лишь его зародыш. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
Впоследствии способность различать друг от друга небольшие совокупности развивалась; появились слова обозначающие числа «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Народные пословицы сохранили память о появлении названий числа 7. К примеру, такие как: «семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ», «семеро одного не ждут» и другие.
Однако когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше семи), заготовленными на зиму. Поэтому счет получил свое дальнейшее развитие.
Способов счета было придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков.
Но палку с зарубками с собой не возьмешь, да и камни таскать не очень приятно, а пастуху нужно знать, не отбилась ли какая коза от стада. И тут на помощь приходят пальцы рук — отличный счетный материал, кстати.
Таким образом, можно сделать первый вывод: древний человек хотел учитывать вещи, которыми он владел. Сколько у него инструментов? Сколько оружия? Сколько животных?
Жизнь наших предков была намного проще, но даже они вынуждены были прибегать к использованию числа.
Продолжая изучать литературу по данной теме, мы заметили, что математика - это не только стройная система законов, но и уникальное средство познания красоты. А красота многогранна и многолика.
Рассмотрим применение математики в окружающей нас жизни.
Глава II. Применение математики в окружающей нас жизни.
§ 1. Математика в мире растений.
Мир растений - величайшее чудо природы, царство красоты и наше целительное богатство. Изучением лекарственных растений занимается наука фитотерапия. Конечно, в этой науке математика играет не последнюю роль. О том, что и здесь применяется математика, мы можем найти сколь угодно много подтверждений. Перелистывая учебник математики, мы с интересом прочитали эту задачу, и хотим её вам представить:
(Приложение 1).
§ 2. Математика в жизни животных и насекомых.
Мир животных и насекомых - богатый и разнообразный мир живых существ. Этот мир, скажете вы, изучает раздел биологии - зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.
Вот, к примеру, пчёлы - удивительное творение природы. Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет (шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.
Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?
Убедиться в том, что математика применяется в изучении жизни животных, мы сможете, решив следующую задачу. (Приложение 2).
§ 3. Математика геометрических тел и фигур.
Тела и фигуры изучает раздел математики, который называется геометрией. Эта наука возникла в Древней Греции исключительно из практических целей, для измерения участков земли. В том, что с фигурами и телами мы имеем дело в жизни, убеждать, думаем, никого не придётся, а вот понять роль математики в этом, Вы сможете, решив следующую задачу (Приложение 3).
§ 4. Математика и культура.
Нам стало интересно, а какое отношение имеет математика к культуре: ведь это и памятники архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать решили с удивительных архитектурных памятников.
Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах - это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.
Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».
Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения примерно )
Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, нежели пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).
Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.
Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».
На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.
Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.
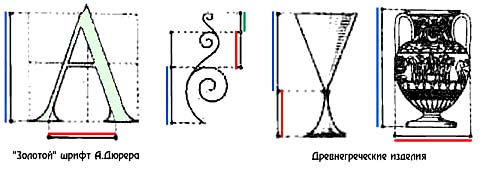
Золотое сечение можно встретить в бытовых предметах и шрифтах.
§ 5. Математика в живой и неживой природе.
Ещё Гете подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно. Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.
Снежинки: ярче примера очаровательной красоты и порядка в природе вы не найдете. Изучением снежинок занимался знаменитый Рене Декарт. А вообще-то, снежинки - это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».
Проанализировав приложение математики в окружающей нас жизни, хочется заметить, что красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность открывать всё новые и новые слагаемые красоты. Так и хочется сказать словами поэта
Все в мире связано в единое начало:
В движенье волн – шекспировский сонет,
В симметрии цветка – основы мирозданья,
А в пенье птиц - симфония планет.
У. Блейк
Изучив весь представленный вам материал, мы поняли, что о математике можно говорить вечно. Наверное, поэтому и символ вечности «∞» (бесконечность) мог появиться только с развитием этой науки «Математика». Мы решили перейти к практической части исследования и для начала провели небольшой социологический опрос, который должен нам помочь подтвердить или опровергнуть выдвинутую ранее гипотезу: если математика второстепенная наука, то законы, которые она изучает знать простому человеку совсем не обязательно, то есть эти законы в обыденной жизни никому не нужны.
Практическая часть
Прежде чем сделать окончательный вывод, что для нас математика, мы предлагаем изучить результаты социологического опроса.
Цель опроса - изучение общественного мнения по данной теме.
Опрос вёлся по следующим направлениям:
1) математика - это жизнь,
2) нужна ли математика в жизни людей,
3) где находит свое применение математика.
Опрос проводился среди следующих категорий:
1) учащиеся 6А, 11А, 11Б СШ № 2,
2) учителя СШ № 2 (выборочно),
3) родители 6А и 11А, 11Б классов (выборочно)
В опросе приняли участие ___100____ человек.
Вот что у нас получилось:
I направление. Математика - это жизнь
Результаты данного направления говорят о том, что математика является жизнью для 90 человек из числа всех опрошенных, для 8 человек математика - это просто наука, 2 человека затруднялись ответить, что для них математика.
II направление. Нужна ли математика в жизни людей?
Нужна ли математика в жизни людей?
Данная диаграмма показывает, что математика нужна 90% (90 человек из 100) и не нужна 10% (10 человек из 100).
III направление. Где находит свое применение математика?
Ответы на этот вопрос приведены в следующей таблице.
17
26
15
11
10
7
9
5
всего: 100 человек
Так отвечали не только дети, но и взрослые.
Заключение
Результаты исследования
Итак, гипотеза, которую мы выдвинули в начале нашего исследования, на практике не подтвердилась. Следовательно, предположение о том, что математика - это второстепенная наука, неверно.
Таким образом, на основании изученной литературы и анализа результатов общественного мнения, мы можем сделать вывод о том, что без знания математики вся современная жизнь невозможна. Например, у нас не было бы хороших домов, т. к. строители должны уметь измерять, считать, сооружать. Наша одежда была бы грубой, т. к. её нужно хорошо скроить. Не было бы ни железных дорог, ни кораблей, ни самолётов, никакой промышленности и тысячи других вещей составляющих часть нашей цивилизации.
В данной работе мы выяснили, математика - часть мира, в котором мы живём.
О мир, пойми! Певцом во сне –
открыты
Закон звезды и формула цветка.
М. Цветаева.
Поэтому мы может с полной и абсолютной уверенностью воскликнуть:
Математика - это жизнь!
Список использованных источников информации
1. За страницами учебника математики. - И. Я. Депман, Н. Я. Виленкин
2. С математикой в путь. - Н. Лэнгдон, Ч. Снейп
3. www.abc-people.com/data/leonardov/zolot_sech-txt.htm - Золотое сечение.
4. http://tmn.fio.ru/works/04x/304/p4_21k.htm - Биология.
5. http://festival.1september.ru/2004_2005/index.php?numb_artic=213063-
История математики.
6. http://bse.sci-lib.com/article048077.html - Золотое сечение.
7. http://www.mjagkov.de/ser/archives/42-,.html
Приложения
Задача № 126
Садовник разложил в три ящика яблоки, сливы и груши. Он написал на ящиках: «яблоки», «сливы», «яблоки и груши», но эти надписи не соответствуют тому, что разложено в каждый ящик. В какой ящик, что разложил садовник?
Решение.
1. Из первого ящика с надписью «яблоки» возьмем один фрукт. Если это яблоко, следовательно, с учетом условия задачи здесь яблоки и груши. Тогда яблоки в ящике с надписью «сливы», а сливы - с надписью «яблоки и груши». Если из первого ящика с надписью «яблоки» вынули сливу, тогда с учетом условия задачи, во втором ящике с надписью «слива» находятся яблоки и груши, а в третьем, с надписью «яблоки и груши» - только яблоки.
2. Аналогично можно выбрать один фрукт из ящика с надписью «яблоки и груши» или «сливы» и с учетом условия задачи, определить в какой ящик, какие фрукты разложил садовник.
Задача № 747*
Три обезьяны за три минуты съели три банана. Сколько бананов съедят шесть обезьян за четыре минуты?
Решение.
1. 3 : 3 = 1 (банан) – съедает за 3 минуты 1 обезьяна
2. 1 : 3 = 1/3 (часть банана) – съедает 1 обезьяна за 1 минуту
3. 6 · 1 = 6 (бананов) – съедят 6 обезьян за 3 минуты
4. 6 · 1/3 = 2 (банана) – съедят 6 обезьян за 1 минуту
5. 6 + 2 = 8 (бананов) – съедят 6 обезьян за 4 минуты
Ответ: 8 бананов.
Задача № 1143. Найти площадь фигуры, вершинами которой будут точки: А(-3;3), В(5;3), С(5;-2) и D(-3;-2) на координатной плоскости. Пусть единичный отрезок будет равен 1 см.
Решение.
Построим на координатной плоскости фигуру АВСD, зная координаты её вершин. Данная фигура является прямоугольником, что мы видим по построению. Чтобы вычислить площадь прямоугольника АВСD нам нужно знать размеры длины и ширины.
Посчитаем, сколько единичных отрезков содержат длина и ширина данного прямоугольника, и учтем, что по условию единичный отрезок будет равен 1 см,
получим: АВ=8(ед.отр.)=8см, ВС=5(ед.отр.)=5см.
Вычислим площадь прямоугольника АВСD по формуле:
S=а·в, S=8·5=40 (см²).
Можно было упростить решение задачи. Учитывая, что фигура задана на координатной плоскости, посчитаем количество квадратиков (как на палетке). Получаем площадь прямоугольника АВСD равна 40 квадратиков (площадь каждого квадратика равна 1).
Ответ: площадь прямоугольника равна 40 см².
В(5;3)
А(-3;3)
С(5;-3)
D(-3;-2)
Х
У
www.metod-kopilka.ru
МАТЕМАТИКА И РАСТЕНИЯ - PDF
Транскрипт
1 МАТЕМАТИКА И РАСТЕНИЯ Исконное значение слова «математика» (от греческого знание, наука) не утрачено и сегодня. Математика была и остается стержнем любой науки, царицей всех наук, символом мудрости. Гармония, симметрия, пропорция, ритм слагаемые прекрасного. Человек во внешнем мире ищет упорядоченность и воспринимает порядок как красоту. Там, где есть порядок, там есть и математика. Можно сказать, что математика есть язык порядка. Математика дает необычайно компактный бесконечно емкий способ выражения научных истин. Десятки страниц научного текста вмещает в себе простая с виду математическая формула. И в этом ее утонченная красота и изящество. Итак, пожелавши, чтобы все было хорошо и ничто по возможности не было дурно, Бог позаботился обо всех видимых вещах, которые пребывали не в покое, но в нестройном и беспорядочном движении; он привел их из беспорядка в порядок, полагая, что второе, безусловно, лучше первого. Платон Всевышний, подобно самому обычному математику или дизайнеру, вынужден был вооружиться если не точной вычислительной техникой, то, по крайней мере, калькулятором. Смех, да и только! а вот приглядитесь к удивительной симметрии и структуре окружающего нас растительного мира, и вы поймете, что шутка эта не так уж и абсурдна. Возьмем, к примеру, соцветие подсолнечника. В нем можно заметить множество перекрещивающихся кривых, близких к дугам логарифмических спиралей. Впервые о логарифмической спирали говорится в одном из писем Рене Декарта в 1683 г. Увидеть ее можно также в завитках раковины. Одно из примечательных свойств логарифмической спирали состоит в том, что произвольный луч, выходящий из ее полюса, пересекает любой виток спирали под одним и тем же углом. Таких спиралей может быть очень много, однако общее количество всегда определенно и в зависимости от вида растения их может быть 34 по часовой стрелке и 55 против, или же соответственно 55 и 89 или 89 и 114. У ананаса 8 спиралей закручены в одну сторону и 5 или 13 в другую. В следующий раз, отправившись в овощной магазин, внимательно взгляните на кочан капусты, соцветие брокколи или головку артишока, и вы опять увидите спирали. Это уж совсем интересно!
2 А теперь займемся арифметикой 8 спиралей в плоде ананаса в одну сторону, 5 в другую, в сумме это дает 13. А если у ананаса соответственно 8 и 13 спиралей, то вместе это составит 21. Расположим эти числа в возрастающем порядке, и у нас получится цепочка 5, 8, 13 и 21 не что иное, как последовательность из так называемого ряда Фибоначчи, впервые описанного выдающимся средневековым итальянским математиком Леонардо Пизанским (Фибоначчи). В этом ряду каждое последующее число равно сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114 и так далее. Вернемся к нашему примеру с подсолнечником количество спиралей, закрученных по и против часовой стрелки и на этот раз соответствует элементам числам ряда Фибоначчи ( ). Практически все соцветья и плотно упакованные ботанические структуры (сосновые и кедровые шишки, ананасы, кактусы, головки подсолнечников и многие другие) также строго следуют числам Фибоначчи. Кроме логарифмической спирали есть еще много интересных кривых 2 го порядка, повторение силуэта которых можно встретить в природе. Известная кривая кардиоида, она обычно не рассматривается в школьном курсе математики, но она такая необычная. Тем более название происходит от слова сердце, и она действительно на сердце похожа. Нарисовать эту кривую просто: возьмите два равных кружочка, вырезанных из фанеры (можно взять две одинаковые монеты). Один из этих кружочков закрепите. Второй приложите к первому, отметьте на краю его точку A, наиболее удаленную от центра первого кружка. Затем катите без скольжения подвижный кружочек по неподвижному и наблюдайте, какую линию опишет точка A. Так и получается кардиоида. В технике эта кривая часто используется для устройства кулачковых механизмов. А в природе ее тоже можно найти в грибную пору. На фотографии перезревший серый мухомор.
3 Синусоида - эта кривая лучше известна школьникам как график функции. Также эту функцию изучают на уроках физики как иллюстрацию колебательных процессов. Но, видимо, колебательные процессы встречаются и в мире живой природы. Поэтому, присмотритесь в лесу к деревьям и кустарникам. Вы обязательно найдете синусоидальные сосны, ветки кустов, рисунки на крыльях некоторых насекомых. Периодические процессы природе не чужды. Также в природе можно найти и циклоиду, и лемнискату, и циссоиду. Розы Гвидо Гранди радуют глаз правильными и плавными линиями, но их очертания не каприз природы они предопределены специально подобранными математическими зависимостями. Семейство роз Гвидо Гранди описывается уравнением в полярных координатах r=a*sin kⱷ. Математический цветник Гвидо Гранди прекрасно иллюстрируется полевыми цветами средней полосы. Замечательным объектом для наблюдения геометрических закономерностей является паутинка. Особенно если вам повезло, и вы видите на ней капельки росы. Паутинка становится более заметной, и вы можете разглядеть прямые линии, которые являются радиусами концентрических окружностей. Провисающая одинокая паутина демонстрирует знаменитую цепную линию. В особых случаях в паутине вы можете разглядеть и треугольники. На уроках
4 физике по этой фотографии вы можете задать вопросы: почему на паутине образуется роса? Почему роса всегда бывает в форме шариков? Почему капельки росы переливаются на солнце? Какие после этого могут быть сомнения в том, что Всевышний по профессии математик! Правда, одновременно он и гениальный художник, созданная им природа не только рациональна, но и прекрасна. А в основе красоты опять же лежит пропорция. Вероятно, вам приходилось слышать термин «золотое сечение» - результат разделения объекта на 2 части таким образом, что меньшая будет относиться к большей так, как большая ко всему объекту. Именно объекты, содержащие в себе золотое сечение, радуют глаз и воспринимаются нами как наиболее гармоничные. Упрощенно это соотношение можно представить как линию длиной 1,618 см, разбитую на 2 отрезка 1 см и 0,618. Величина 1,618 и есть формула золотого сечения. А теперь разделите несколько пар соседних чисел из последовательности Фибоначчи (к примеру, 21:13, 89:55, 144:89), и вы заметите (особенно с ростом последовательности), что соотношение всегда будет или 1,618 или близко к этой величине. Таким образом, оказывается, что золотая пропорция заложена и в последовательности Фибоначчи, в результате чего отражающие ее растительные структуры соответствуют законам красоты и гармонии. У большинства растений цветки и листья образуются из растущей верхушки (меристемы), по кругу перемещаясь от нее по мере роста структуры. Каждый новый зачаток (примордия) появляется из центра и растет под углом от полного оборота по отношению к предыдущему образованию, в результате чего возникают спирали, при этом новые зачатки появляются над старыми, последние остаются внизу спирали, а самая новая примордия оказывается в верхней точке роста структуры. Компьютерная визуализация этой модели развития показывает, что спираль образуется только в том случае, если угол между каждым новым образованием будет с высокой точностью соответствовать величине 137,5. Отклонение от этого угла лишь на одну десятую градуса мгновенно разрушит всю спиралевидную структуру. Если мы разделим полный круг (365 ) в золотой пропорции, то в результате получатся два угла 222,5 и 137,5. И, наконец, главный вопрос почему? Почему последовательность Фибоначчи и пропорция золотого сечения так настойчиво проявляются в природе? Впрочем, ни одно правило не обходится без исключений, существует так называемая «аномальная» группа растений с цветками, количество лепестков в которых равно 4, 7, 11, 18 или удвоенным числам Фибоначчи.
5 Примордии рождаются из меристемы в виде одноклеточных зачатков, при этом их положение относительно окружающих клеток определяет, чем они станут в будущем листьями, цветками или иными органами растительной структуры. Каждая новая примордия появляется там, где промежуток между уже образовавшимися зачатками наибольший, в результате чего для успешного роста ей будет достаточно минимальной энергии. Для примера рассмотрим рост листьев на ветке. Каждый новый лист на кончике ветки получает солнечный свет, однако при этом желательно, чтобы он как можно меньше затенял предыдущие листья. Если листья располагаются на ветке по спирали в соответствии с пропорцией золотого сечения, под углом 137,5, то в этом случае солнечный свет используется ими максимально. Поскольку закон сохранения энергии один из фундаментальных в живой природе, то в своем развитии растения попросту выбирают путь наименьшего сопротивления, спиральная структура дает им явное эволюционное преимущество, а красота и элегантность достигаемого при этом визуального эффекта настоящий гимн природе, которая всегда находит наиболее экономичное решение для любой проблемы. Леонардо да Винчи вывел правило, согласно которому квадрат диаметра ствола дерева равен сумме квадратов диаметров ветвей, взятых на общей фиксированной высоте. Более поздние исследования подтвердили его с одним лишь отличием степень в формуле необязательно равняется 2, а лежит в пределах от 1,8 до 2,3. Традиционно считалось, что эта закономерность объясняется тем, что у дерева с такой структурой оптимальный механизм снабжения веток питательными веществами. Однако в 2010 году американский физик Кристоф Эллой нашѐл более простое механическое объяснение феномену. В своей работе Эллой использовал простой механический подход. Он рассмотрел дерево как фрактал (фигуру, обладающую некоторой степенью самоподобия), причем каждая ветка моделировалась как балка со свободным концом. В этих предположениях (а также при условии постоянства по времени вероятности слома ветки под воздействием ветра) оказалось, что закон Леонардо минимализирует вероятность того, что ветки дерева сломаются под напором ветра. Коллеги физика отметили, что его механическое объяснение обладает, в отличие от связанного со снабжением питательными веществами, "элегантностью и простотой". При этом они отмечают, что объяснение лежало на поверхности, однако до него никто раньше не додумался. Вы знаете, что расположение листьев на стеблях также носит строгий математический характер и это явление называется в ботанике "филлотаксисом". В явлении филлотаксиса используются более сложные понятия симметрии, в частности понятие "винтовая ось симметрии". Рассмотрим, например,
6 расположение листьев на стебле растения (Рис.1). Мы видим, что листья находятся на различных высотах стебля вдоль винтовой линии, обвивающейся вокруг его поверхности. Для того чтобы перейти от нижележащего листа к следующему, приходится мысленно повернуть лист на некоторый угол вокруг вертикальной оси стебля, а затем поднять его на определенный отрезок вверх. В этом и состоит суть "винтовой симметрии". Рисунок 1.Винтовая симметрия. Рисунок 2. Винтовые оси на стеблях растений. А теперь рассмотрим характерные "винтовые оси", которые возникают на стеблях растений (Рис.2). На Рис.2-а изображен стебель растения с винтовой осью симметрии третьего порядка. Проследим линию листорасположения на этом рисунке. Для того, чтобы перейти от листа 1 к листу 2, следует повернуть первый вокруг оси стебля на 120 против часовой стрелки (если смотреть снизу) и затем передвинуть листок 1 вдоль стебля по вертикали до тех пор, пока он не совместится с листком 2. Повторяя подобную операцию, перейдем от листа 2 к листу 3, а затем к листу 4. Обратим внимание на то, что листок 4 лежит над листком 1 (как бы повторяет его, но этажом выше) и что, идя от листа 1 к листу 4, мы трижды совершили поворот на угол 120, т.е. осуществили полный оборот вокруг оси стебля (120 * 3 = 360 ). Угол поворота винтовой оси у ботаников называется "углом расхождения листьев". Вертикальная прямая, соединяющая два листа, расположенные друг над другом на стебле, именуется "ортостихой". Отрезок 1-4 ортостихи соответствует полной трансляции винтовой оси. Как мы увидим далее, число оборотов вокруг оси стебля для перехода от нижнего листа к вышележащему, расположенному в точности над нижним (по ортостихе), может равняться не только единице, но и двум, трем и т.д. Это число оборотов называется "листовым циклом". В ботанике принято характеризовать винтовое листорасположение с помощью дроби, числителем которой является число оборотов в листовом цикле, а знаменателем -
7 число листьев в этом цикле. В рассмотренном нами случае мы имеем винтовую ось типа 1/3. На Рис.2-б изображена пятерная винтовая ось симметрии с листовым циклом 2 (для перехода от листа 1 к листу 6 надо совершить два полных оборота). Дробь, характеризующая данную ось, равна 2/5; угол расхождения листьев составляет 144 (360 : 5 = 72 ; 72 * 2 = 144 ). Заметим, что существуют и более замысловатые оси, например, типа 3/8, 5/13 и т.д. Возникает вопрос, какими могут быть числа a и b, характеризующие винтовую ось типа a/b. И вот здесь Природа преподносит нам очередной сюрприз в виде так называемого "Закона филлотаксиса". Ботаники утверждают, что дроби, характеризующие винтовые оси растений, образуют строгую математическую последовательность, состоящую из отношений соседних чисел Фибоначчи, то есть: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34 Дроби в последовательности (1) образуются числами Фибоначчи, взятыми через одно число. Ботаники установили, что для различных растений характерны свои дроби филлотаксиса из последовательности (1). Например, дробь 1/2 свойственна злакам, березе, винограду; 1/3 - осоке, тюльпану, ольхе; 2/5 - груше, смородине, сливе; 3/8 - капусте, редьке, льну; 5/13 - ели, жасмину и т.д. Какова же "физическая" причина, лежащая в основе "законов филлотаксиса"? Ответ очень прост. Оказывается, что именно при таком расположении листьев достигается максимум притока солнечной энергии к растению. Но не только растения, но и некоторые животные, например, змеи используют те же принципы в организации своих внешних форм. Таким образом, строгую математику мы находим и в расположении лепестков на цветке розы и в разрезе яблока (пентаграмма), и в сосновой шишке, и в головке подсолнечника. И мы снова и снова убеждаемся в том, что все в природе подчинено единому плану, единым законам - и раскрыть и объяснить эти законы и есть главная задача человеческой науки. Это траектория передвижения беззубки, оставленная на песке в течение 3-х суток. Рассчитайте среднюю скорость движения этого моллюска.
8 Практическая часть Вычислим площадь фигуры, ограниченной кардиоидой r=a(1+,. S= I=
docplayer.ru
Научно-исследовательская работа по математике на тему: "С математикой по жизни!"
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа № 4
г.Нелидово Тверской области

Выполнил: ученик 7а класса
Колеватых Александр
Руководитель работы: Орлова Ольга Геннадьевна
2016 г.
Объект исследования:живая и не живая природа.Предмет исследования: необходимость выяснить, существует ли взаимосвязь математики и окружающего мира. Гипотеза:«Все, что нас окружает, можно представить и понять с помощью чисел».Методы исследования:- поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет;- анкетирование, сбор информации, анализ полученных в ходе исследования данных;
- подбор задач, подтверждающих связь математики с жизнью.
Цель работы:доказать, что математика – это неотъемлемая часть в жизни человечества.Задачи:
- рассмотреть взаимосвязь между математикой и жизнью;
- проанализировать, как жизнь зависит от математики;
- развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала;
- обобщить собранную информацию и познакомить с ней своих одноклассников;
- сделать вывод о подтверждении или опровержении выдвинутой гипотезы.
Актуальность изучения данной темы заключается в том, что без математики не обойтись, без знания математики вся современная жизнь невозможна.
Содержание:
Введение.
2. Из истории возникновения математики.
3.Применение математики в окружающей нас жизни.
а) Математика в мире растений.
б) Математика в жизни животных и насекомых.
в) Математика геометрических тел и фигур.
г) Математика и культура.
д) Математика в живой и неживой природе.
4. Практическая часть.
5. Выводы и заключение.
6. Литература.
1.ВВЕДЕНИЕ
Мы часто задаемся вопросом: «Зачем мы изучаем математику? Какое место в нашей жизни она занимает?»
Может быть это жизнь, а может быть это просто наука, которая является для нас второстепенной.
Древнегреческий философ Платон сказал, обращаясь к своему ученику: “Разве ты не заметил, что способный к математике изощрен ко всем наукам в природе?”
Он же заметил: “Было бы не плохо, если бы лиц, занимающих высшие государственные должности, приучали заниматься математикой и в нужных случаях к ней обращаться”
Ему вторил через много веков М.И. Калинин (с 1938–1945 председатель Президиума Верховного Совета СССР): “Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе”.
Наверное, хотя бы один раз в своей жизни каждый ученик задавал себе вопрос: «Зачем мне изучать математику? Научился считать и достаточно!»
В своей работе я попытался выяснить, так что же для нас математика? Может быть, это жизнь, а может быть, это просто наука, которая является для нас второстепенной и заниматься ею нужно только ученым?
Своё исследование я решил начать с изучения истории математики.
2.ИЗ ИСТОРИИ ВОЗНИКНОВЕНИЯ МАТЕМАТИКИ
Учёные - археологи обнаружили стойбище древних людей. В нём они нашли волчью кость, на которой 30 тысяч лет назад какой - то древний охотник нанёс 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам.
Много тысячелетий прошло с тех пор. Но и сейчас швейцарские крестьяне, отправляя молоко на сыроварню, отмечают число фляг такими, же зарубками. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером, которой отмечают товар. А ещё 200 - 300 лет тому назад так называли куски дерева, на которых зарубками отмечали сумму долга. Бирку с зарубками раскалывали пополам. При расчёте половинки складывались вместе, и это позволяло определить сумму долга без споров и сложных вычислений.
Первыми понятиями математики, с которыми столкнулись люди, были «меньше», «больше», «столько же». Если одно племя меняло рыбу на сделанные другим племенем каменные ножи, достаточно было положить рядом с каждой рыбой один нож, соответствующий величине рыбы, чтобы сделка состоялась.
А вот так выглядело счётное устройство инков, которое состояло из узелков, завязанных на веревках разной длины. Если внимательно приглядеться, то эти узелки чем-то отдаленно напоминают счеты.

Для запоминания результатов счёта использовали зарубки, узелки и т. п.
Были и более экзотичные варианты. Например, такие математические таблицы древних, обнаружены на территории современной Армении.
Одна из древнейших нумераций, дошедших до нас в древних папирусах и рисунках, была – египетская.

Для записи чисел египтяне использовали картинки-иероглифы.
Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта и подчинении его власти Александра Македонского.
Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел. Недаром ведь говорят: «Без названия нет знания».
О том, как появились имена у чисел, учёные узнают, изучая языки разных народов и племён. Ведь, как известно, учёные считают, что сначала названия получили числа 1 и 2.
Когда римляне (в древности они говорили на латыни) придумывали имя числу 1(солюс), они исходили из того, что Солнце на небе одно. А название для числа 2 во многих языках связано с предметами, встречающимися попарно, - крыльями, ушами, руками и т.д.
А есть более экзотичные варианты.
Например, на языке некоторых папуасских племён (о. Новая Гвинея) числа назвали так: 1 - «урапун», 2 - «оказа», 3 - «оказа -урапун», 4 - «оказа - оказа», 5 - «оказа - оказа - урапун», 6 - «оказа - оказа - оказа» и «много», как самое большое число. Правда, интересно! Но тогда как, же считать такими числами расстояния до звезд, размеры галактики, или как этими числами папуасские племена обозначали бы мельчайшие размеры атома?!
§ 2. Античная математика.
Третий век до нашей эры был золотым веком античной математики.
В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию.
В III веке до н. э. в городе Александрия Птолемей I основал Дом Муз и пригласил туда виднейших учёных. Это была первая академии, с богатейшей библиотекой, которая к I веку до н. э. насчитывала 70000 книг.
Но самая громкая слава выпала на долю трёх великих геометров античной математики – это, конечно же, Евклид, Архимед и Апполоний Пергский. Евклид (написал книгу «Начала», авторитет которой был и остается огромным более 2000 лет), Архимед (развил метод вычисления площадей и объёмов геометрических фигур и тел), Аполлоний Пергский (автор исследования сечений геометрических тел).
А такие два достижения греческой математики далеко пережили своих творцов.
1) греки построили и представили миру математику как целостную науку;
2) греки провозгласили, что законы природы постижимы для человеческого разума.
§3. Страны ислама
Математика Востока, в отличие от греческой, всегда носила более практический характер. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика. Преследование греческих учёных-нехристиан в Римской империи V—VI веков вызвало их массовое бегство на восток, в Персию и Индию. При дворе Хосрова I они переводили античных классиков на сирийский язык, а два века спустя появились арабские переводы этих трудов. Так было положено начало ближневосточной математической школе. Большое влияние на неё оказала и индийская математика, также испытавшая сильное древнегреческое влияние. В начале IX века научным центром халифата становится Багдад, где халифы создают «Дом мудрости», в который приглашаются виднейшие учёные всего исламского мира —сабии (потомки вавилонских жрецов-звездопоклонников), тюрки и другие. На западе халифата, в испанской Кордове, сформировался другой научный центр, благодаря которому античные знания стали понемногу возвращаться в Европу. Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, были задачи о расчёте лунного календаря, об определении киблы — точного направления на Мекку.
В целом, эпоха исламской цивилизации в математических науках может быть охарактеризована не как эпоха поиска новых знаний, но — как эпоха передачи и улучшения знаний, полученных от греческих математиков.
§4. Средневековье, IV - XV века
В это время мы можем отметить расцвет математики как науки.
В конце XII века на базе нескольких монастырских школ был создан Парижский университет. Возникают Оксфорд и Кембридж в Британии.
Первым крупным математиком средневековья стал Леонардо Пизанский, известный под прозвищем Фибоначчи.
§5. Математика у русского народа
Интерес к науке на Руси появился рано. Сохранились сведения о школах при Владимире Святославовиче и Ярославе Мудром (XI век).
Русский народ создал свою собственную систему мер:
1 миля = 7 верстам ( 7,47 км)
7,47 км)
1 верста = 500 саженям ( 1,07 км)
1,07 км)
1 сажень = 3 аршинам = 7 футам ( 2,13 м)
2,13 м)
1 аршин = 16 вершкам = 28 дюймам ( 71,12 см)
71,12 см)
1 фут = 12 дюймам ( 30,48 см)
30,48 см)
1 дюйм = 10 линиям ( 2,54 см)
2,54 см)
1 линия = 10 точкам ( 2,54 мм).
2,54 мм).
Интересно, что на Руси когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см, или о богатырях говорили «Богатырь, косая сажень в плечах», т.е. у такого человека по диагонали от мизинца левой руки до пятки правой ноги почти 2 метра 13 сантиметров.
§ 6. Искусство счета.
Изучив этот материал, мы поняли, что искусство счета развивалось с развитием человечества. На ранних ступенях развития общества люди почти не умели считать. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Это был еще не счет, а лишь его зародыш. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
Впоследствии способность различать друг от друга небольшие совокупности развивалась; появились слова обозначающие числа «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Народные пословицы сохранили память о появлении названий числа 7. К примеру, такие как: «семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ», «семеро одного не ждут» и другие.
Однако когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше семи), заготовленными на зиму. Поэтому счет получил свое дальнейшее развитие.
Способов счета было придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков.
Но палку с зарубками с собой не возьмешь, да и камни таскать не очень приятно, а пастуху нужно знать, не отбилась ли какая коза от стада. И тут на помощь приходят пальцы рук — отличный счетный материал, кстати.
Таким образом, можно сделать первый вывод: древний человек хотел учитывать вещи, которыми он владел. Сколько у него инструментов? Сколько оружия? Сколько животных?
Жизнь наших предков была намного проще, но даже они вынуждены были прибегать к использованию числа.
Продолжая изучать литературу по данной теме, я заметил, что математика - это не только стройная система законов, но и уникальное средство познания красоты. А красота многогранна и многолика.
Рассмотрим применение математики в окружающей нас жизни.
3.ПРИМЕНЕНИЕ МАТЕМАТИКИ В ОКРУЖАЮЩЕМ НАС МИРЕ
§ 1. Математика в мире растений.
«Природа формулирует свои законы языком математики» Г.Галилей.
Математика – удивительная и интересная наука, которую многие люди считают слишком сложной для освоения, а потому скучной и неинтересной. Тем не менее, математикой пользуются существа, которых разумными назвать очень сложно.
Более того, недавно британские ученые поведали миру о потрясающем открытии. Математическими расчетами пользуются растения! Математика позволяет им регулировать запасы питательных веществ в ночное время.
Обнаружив биологический пример сложных арифметических расчетов, исследователи из расположенного в Норидже, Великобритания независимого международного Центра Джона Иннеса (John Innes Centre ) были поражены. Как следует из опубликованного в журнале e-Life научного отчета, математические модели показывают, что количество крахмала, потребляемого растениями каждой ночью, рассчитывается ими исходя из наличия запаса. Возможно, подобные механизмы могут использовать птицы, рачительно расходуя жир во время миграций.

Свои способности в ходе экспериментов ученым демонстрировал скромный сорняк, родственник горчицы и капусты Arabidopsis или резушка. Растение-космонавт, рекордсмен Книги Гиннесса известно тем, что в 1982 году впервые зацвело на космической станции Салют-7 и дало жизнеспособные семена, пророщенные на Земле спустя 10 лет.
Как известно, ночью, когда нет солнечно света, растения потребляют запасенные ими углеводы, регулируя потребление таким образом, чтобы протянуть до рассвета. Эксперименты ученых из Центра Джона Иннеса показывают, что для точной корректировки потребления крахмала растения должны выполнять арифметическое действие - деление.
«Они в самом деле используют математику простым химическим способом, что удивительно», - рассказала руководитель исследования профессор Элисон Смит (Alison Smith). «Это действие из программы начальной школы, но все же они используют математику».
Чтобы определить, каким образом осуществляют расчеты растения, ученые применили методы математического моделирования.
В течение ночи некий механизм растения контролирует запас крахмала. Информация о времени поступает от внутренних биологических часов, наподобие тех, что есть у человека. По мнению исследователей, процесс связан с концентрацией двух видов молекул, названных S для крахмала и T для времени. Если S-молекулы стимулируют расход крахмала, то Т-молекулы, напротив, препятствуют этому. Таким образом, скорость процесса расходования питательного вещества задается соотношением молекул S и T, или S деленное на T.
«Это первый конкретный пример таких сложных арифметических подсчетов в биологии», - считает профессор математики Мартин Говард (Martin Howard) из Центра Джона Иннеса.
Ученые предполагают, что аналогичные механизмы могут использоваться животными, например птицами для контроля жировых запасов в ходе миграций или вынужденного бездействия во время высиживания яиц.
Комментируя исследование коллег, доктор Ричард Баггс (Richard Buggs) из лондонского Университета Королевы Марии (Queen Mary University of London) сказал: «Это не является доказательством наличия интеллекта у растений. Просто растения обладают механизмом для автоматического регулирования интенсивности потребления углеводов ночью. Растения не способны выполнять математические действия добровольно и с определенной целью, как это делаем мы».
(По материалам BBC)
Приглядимся к удивительной симметрии и структуре окружающего нас растительного мира. Возьмем, к примеру, соцветие подсолнечника. В нем можно заметить множество перекрещивающихся спиралей. Их может быть очень много, однако общее количество всегда определенно и в зависимости от вида растения их может быть 34 по часовой стрелке и 55 против, или же соответственно 55 и 89 или 89 и 114. К ананаса 8 спиралей закручены в одну сторону и 5 или 13 в другую. В следующий раз, отправившись в овощной магазин, внимательно взгляните на кочан капусты, соцветие брокколи или головку артишока, и вы опять увидите спирали. Это уж совсем интересно! А теперь займемся арифметикой – 8 спиралей в плоде ананаса в одну сторону, 5 в другую, в сумме это дает 13. А если у ананаса соответственно 8 и 13 спиралей, то вместе это составит 21. Расположим эти числа в возрастающем порядке, и у нас получится цепочка 5, 8, 13 и 21 – не что иное как последовательность из так называемого ряда Фибоначчи, впервые описанного выдающимся средневековым итальянским математиком Леонардо Пизанским (Фибоначчи). В этом ряду каждое последующее число равно сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114 и так далее. Вернемся к нашему примеру с подсолнечником – количество спиралей, закрученных по и против часовой стрелки и на этот раз соответствует элементам числам ряда Фибоначчи.
(34 – 55 – 89 – 114).
Ещё Гете подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно. Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.



Какие после этого могут быть сомнения в том, что Всевышний по профессии математик! Правда, одновременно он и гениальный художник, созданная им природа не только рациональна, но и прекрасна. А в основе красоты лежит опять же пропорция.
§ 2. Математика в жизни животных и насекомых.
Мир животных и насекомых - богатый и разнообразный мир живых существ. Этот мир, скажете вы, изучает раздел биологии - зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.




Вот, к примеру, пчёлы - удивительное творение природы. Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет (шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.
Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?



§ 3. Математика геометрических тел и фигур.



Тела и фигуры изучает раздел математики, который называется геометрией. Эта наука возникла в Древней Греции исключительно из практических целей, для измерения участков земли. В том, что с фигурами и телами мы имеем дело в жизни, убеждать, думаем, никого не придётся.
Например, кристаллы поваренной соли имеют форму куба, кристаллы льда и горного хрусталя (кварца) напоминают отточенный с двух сторон карандаш, т.е. имеют форму шестиугольной призмы, на основания которой поставлены шестиугольные пирамиды.
Алмаз чаще всего встречается в виде октаэдра, иногда куба и даже кубооктаэдра. Исландский шпат, который раздваивает изображение, имеет форму косого параллелепипеда. Пирит – куб или октаэдр, иногда встречается в виде усеченного октаэдра.



§ 4. Математика и культура.
Мне стало интересно, а какое отношение имеет математика к культуре: ведь это и памятники архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать я решил с удивительных архитектурных памятников.
Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах - это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.
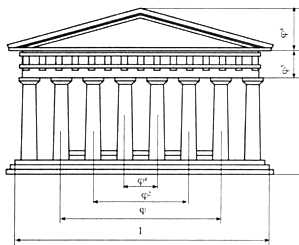

Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».
Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.



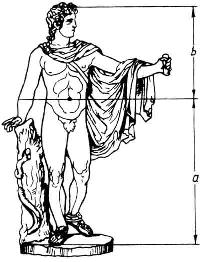
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения примерно 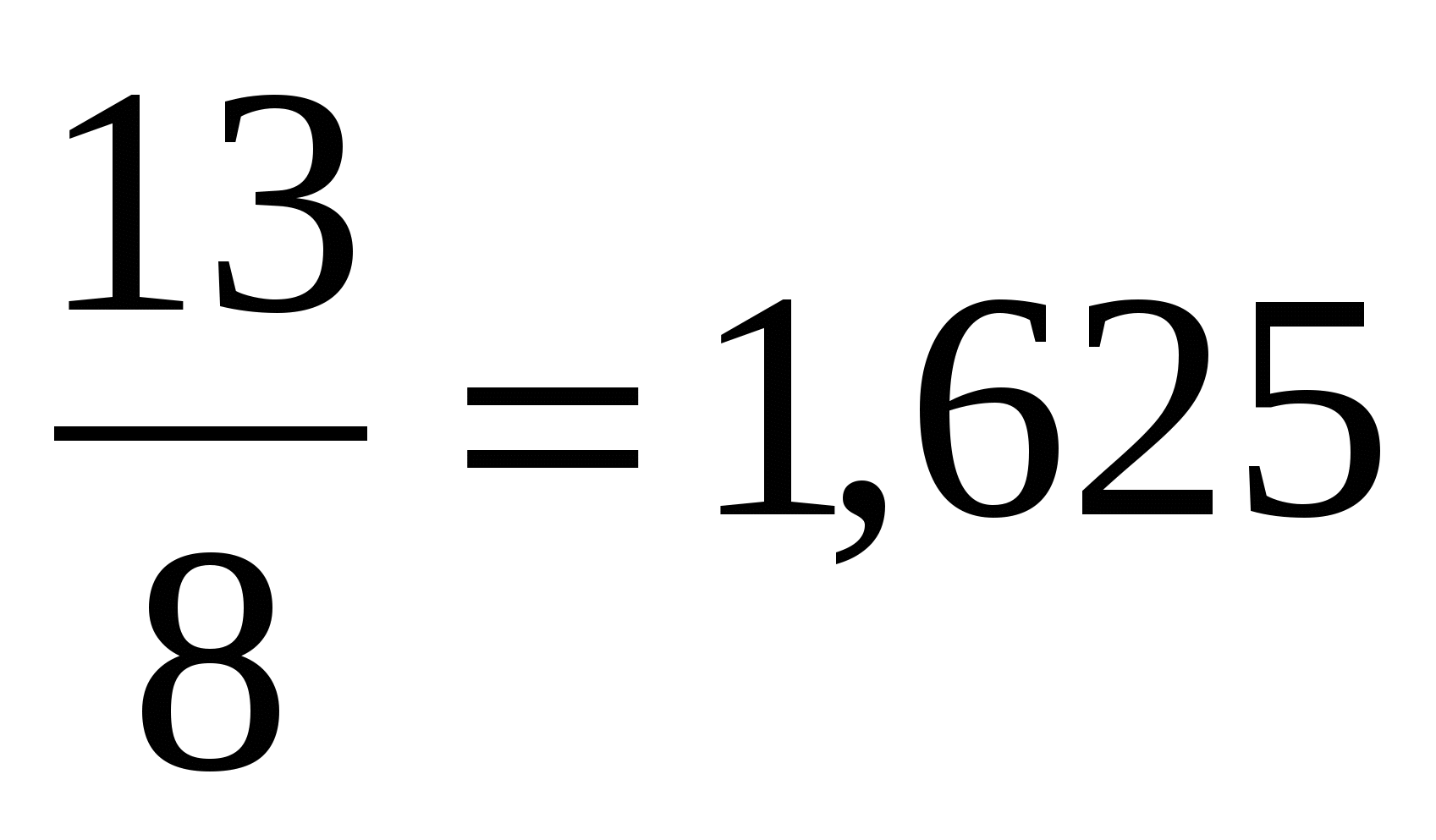 )
) 
Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, нежели пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).
Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.
Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».

На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.

Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.
Золотое сечение можно встретить в бытовых предметах и шрифтах.
Математика в живой и неживой природе.
Снежинки: ярче примера очаровательной красоты и порядка в природе вы не найдете. Изучением снежинок занимался знаменитый Рене Декарт. А вообще-то, снежинки - это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».




5.Математика и музыка.
Математика – царица наук, тесным образом перекликается с музыкой. Несомненно, математика пронизывает музыку.
Музыка и ее первый звук родились одновременно с творением мира, как утверждали древние мудрецы.
В своих трудах ученые неоднократно делали попытки представить музыку как некую математическую модель. Приведем, к примеру, одну из цитат из работы Леонарда Эйлера “Диссертация о звуке”, написанная в 1727 году: “Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке из правильных оснований все, что может сделать приятным объединение и смешивание звуков”.
Свое отношение к математике и музыки ученые высказывались в своих личных переписках. Так, к примеру, Лейбниц в письме Гольдбаху пишет: “Музыка есть скрытое арифметическое упражнение души, не умеющей считать”. На что Гольдбах ему отвечает: “Музыка – это проявление скрытой математики”.
Однако, одним из первых, кто попытался выразить красоту музыки с помощью чисел, был Пифагор.
Известно открытие Пифагора в области теории музыки. Необычность его в том, что сочетание звуков, издаваемых струнами, наиболее благозвучно, если длины струн музыкального инструмента находятся в правильном численном отношении друг к другу.
Для воплощения своего открытия Пифагор использовал монохорд - полуинструмент, полуприбор. Под струной на верхней крышке ученый начертил шкалу, с помощью которой можно было делить струну на части. Было проделано много опытов, в результате которых Пифагор описал математически звучание натянутой струны.
Оказывается, длины трёх струн, дающих ноты до,ми, соль образуют арифметическую пропорцию. Именно длины струн относятся, как число
1 : 4/5 : 2/3.

Приятные для слуха созвучия подчиняются простым математическим законам.
Позже учёные – математики создали теорию музыки.
Проанализировав приложение математики в окружающей нас жизни, хочется заметить, что красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность открывать всё новые и новые слагаемые красоты. Так и хочется сказать словами поэта
Все в мире связано в единое начало:
В движенье волн – шекспировский сонет,
В симметрии цветка – основы мирозданья,
А в пенье птиц - симфония планет.
У. Блейк
Изучив весь представленный вам материал, я понял, что о математике можно говорить вечно. Наверное, поэтому и символ вечности «∞» (бесконечность) мог появиться только с развитием этой науки «Математика». Я решил перейти к практической части исследования и для начала провел небольшой социологический опрос, который должен нам помочь подтвердить или опровергнуть выдвинутую ранее гипотезу: «Все, что нас окружает, можно представить и понять с помощью чисел».
5.ПРАКТИЧЕСКАЯ ЧАСТЬ.
I направление. Нужна ли математика в жизни людей?
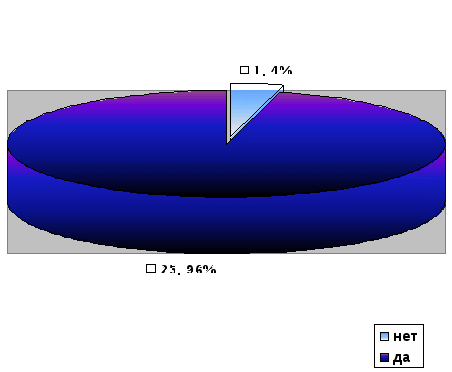




Нужна ли математика в жизни людей?

Данная диаграмма показывает, что математика нужна 96% (25 человек из 26) и не нужна 4 % (1 человек из 26).
II направление.
Зачем мне надо изучать математику?
Школьники ответили так:
Необходима для продолжения обучения и приобретения профессии
23 человека
Для общего развития
16 человек
Этот предмет мне интересен
3 человека
Не знаю, зачем
1 человек
III направление. Где находит свое применение математика?
Ответы на этот вопрос приведены в сл
infourok.ru
Научный проект Тема: «Математика это жизнь»
Коммунальное государственное учреждение«Средняя школа № 2» Городского отдела образования акимата г. Тараз
Научный проект
Тема: «Математика - это жизнь»
Авторы:
Хабибулина Регина,
Смирнова Екатерина,
ученицы 6 «А» класса
Секция: математика
Руководитель:
Хабибулина Л.В.
2012-2013 учебный год
Оглавление
- Отзыв о работе.
3. Теоретическая часть:
Вступление.
Глава I. Из истории возникновения математики.
§ 1. Возникновение арифметики и теории чисел.
§ 2. Античная математика.
§ 3. Страны ислама.
§ 4. Математика средневековья: IV-XV века.
§ 5. Математика на Руси.
§ 6. Искусство счета.
Глава II. Применение математики в окружающей нас жизни.
§ 1. Математика в мире растений.
§ 2. Математика в жизни животных.
§ 3. Математика геометрических тел и фигур.
§ 4. Математика и культура.
§ 5. Математика в живой и неживой природе.
4. Практическая часть
5. Заключение
6. Список использованных источников информации
7. Приложения
Введение
Данная работа относится к разделу проблемно - исследовательскому.
Цель работы: выяснить, что значит математика в жизни людей: является второстепенной наукой или математика – это неотъемлемая часть в жизни человечества.
^
1) рассмотреть взаимосвязь между математикой и жизнью,
2) проанализировать, как жизнь зависит от математики.
Гипотеза: если математика - второстепенная наука, то законы, которые она изучает знать простому человеку совсем не обязательно, то есть эти законы в обыденной жизни никому не нужны.
^ если гипотеза подтверждается, то можно утверждать, что без математики можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.
Методы исследования:
- изучение и анализ литературы по данной теме;
- подбор задач, подтверждающих связь математики с жизнью;
- сбор и анализ общественного мнения.
Теоретическая часть
Вступление.
На уроке математики нам поручили подготовить проект. Работая над проектом, мы долго не могли определиться с его темой. Нам все было интересно. Так, изучив в 5-м классе простые и составные числа, нам стало интересно, а есть ли число, которое больше вселенной? Ведь при этом нужно учитывать тот факт, что каждое следующее число больше предыдущего хотя бы на единицу. Оказалось очень трудным делом найти самое большое число. Такие числа оказалось для нас не только трудно прочитать, но и записать. А как же с такими числами, спросите Вы, можно выполнять арифметические действия? Ну конечно, ответят им многие, ведь современные компьютеры достигли потрясающих скоростей быстродействия. Поэтому некоторым, кажется, что в современном мире все можно просчитать, достаточно только взять компьютер помощнее. Но это не так.
Ведь до сих пор в мире нет признанной всеми системы наименований больших и сверхбольших чисел. А в словарях, кроме центиллиона, нет названий для чисел, имеющих порядок больше 63 (такое число называют вигинтиллионом).
Свою систему наименований для чисел предлагал Архимед. С ее помощью он мог именовать числа вплоть до 1080000000000000000, которое он называл «последним числом».
Изучив это, мы убедились в том, что попытка найти самое большое число приводит нас в тупик, так как к любому числу достаточно всего лишь прибавить единицу, чтобы получить число большее данного.
Из всего этого мы поняли, что человека окружает громадное количество фактов и явлений, которые в силу своей огромности кажутся далекими и недоступными пониманию, но при глубоком изучении становятся близкими, интересными, загадочными.… И тут нас осенило.
Эврика! Все в мире и в жизни тесно связано с математикой! Вот и нашлась прекрасная тема для проекта: «Математика в жизни людей», или «Математика – это жизнь»
Мы специально не ставим никакого знака препинания в конце предложения, так как считаем, что эту фразу можно произнести с разной интонацией: кто–то её произнесет вопросительно, кто–то с восклицанием, а кто–то просто повествовательно.
В своей работе мы попытаемся выяснить, так что же для нас математика? Может быть, это жизнь, а может быть, это просто наука, которая является для нас второстепенной и заниматься ею нужно только ученым?
Своё исследование мы решили начать с изучения истории математики.
^
§ 1. Возникновение арифметики и теории чисел.
Учёные - археологи обнаружили стойбище древних людей. В нём они нашли волчью кость, на которой 30 тысяч лет назад какой - то древний охотник нанёс 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам.
Много тысячелетий прошло с тех пор. Но и сейчас швейцарские крестьяне, отправляя молоко на сыроварню, отмечают число фляг такими, же зарубками. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером, которой отмечают товар. А ещё 200 - 300 лет тому назад так называли куски дерева, на которых зарубками отмечали сумму долга. Бирку с зарубками раскалывали пополам. При расчёте половинки складывались вместе, и это позволяло определить сумму долга без споров и сложных вычислений.
Первыми понятиями математики, с которыми столкнулись люди, были «меньше», «больше», «столько же». Если одно племя меняло рыбу на сделанные другим племенем каменные ножи, достаточно было положить рядом с каждой рыбой один нож, соответствующий величине рыбы, чтобы сделка состоялась.
А вот так выглядело счётное устройство инков, которое состояло из узелков, завязанных на веревках разной длины. Если внимательно приглядеться, то эти узелки чем-то отдаленно напоминают счеты.
Для запоминания результатов счёта использовали зарубки, узелки и т. п.
Были и более экзотичные варианты. Например, такие математические таблицы древних, обнаружены на территории современной Армении.
Одна из древнейших нумераций, дошедших до нас в древних папирусах и рисунках, была – египетская.
Для записи чисел египтяне использовали картинки-иероглифы, означавшие буквально следующее:
- собственно 1. - 10. - 100. - 1 000. - 10 000. - 100 000. - 1 000 000. - 10 000 000.
К примеру, число 2253 на этой картинке было изображено так:
- две тысячи, две сотни, пять десятков и три единицы.
Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта и подчинении его власти Александра Македонского.
Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел. Недаром ведь говорят: «Без названия нет знания».
О том, как появились имена у чисел, учёные узнают, изучая языки разных народов и племён. Ведь, как известно, учёные считают, что сначала названия получили числа 1 и 2.
Когда римляне (в древности они говорили на латыни) придумывали имя числу 1(солюс), они исходили из того, что Солнце на небе одно. А название для числа 2 во многих языках связано с предметами, встречающимися попарно, - крыльями, ушами, руками и т.д.
А есть более экзотичные варианты.
Например, на языке некоторых папуасских племён (о. Новая Гвинея) числа назвали так: 1 - «урапун», 2 - «оказа», 3 - «оказа -урапун», 4 - «оказа - оказа», 5 - «оказа - оказа - урапун», 6 - «оказа - оказа - оказа» и «много», как самое большое число. Правда, интересно! Но тогда как, же считать такими числами расстояния до звезд, размеры галактики, или как этими числами папуасские племена обозначали бы мельчайшие размеры атома?!
§ 2. Античная математика.
Третий век до нашей эры был золотым веком античной математики.
В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию.
В III веке до н. э. в городе Александрия Птолемей I основал Дом Муз и пригласил туда виднейших учёных. Это была первая академии, с богатейшей библиотекой, которая к I веку до н. э. насчитывала 70000 книг.
Но самая громкая слава выпала на долю трёх великих геометров античной математики – это, конечно же, Евклид, Архимед и Апполоний Пергский. Евклид (написал книгу «Начала», авторитет которой был и остается огромным более 2000 лет), Архимед (развил метод вычисления площадей и объёмов геометрических фигур и тел), Аполлоний Пергский (автор исследования сечений геометрических тел).
А такие два достижения греческой математики далеко пережили своих творцов.
1) греки построили и представили миру математику как целостную науку;
2) греки провозгласили, что законы природы постижимы для человеческого разума.
§3. Страны ислама
Математика Востока, в отличие от греческой, всегда носила более практический характер. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика. Преследование греческих учёных-нехристиан в Римской империи V—VI веков вызвало их массовое бегство на восток, в Персию и Индию. При дворе Хосрова I они переводили античных классиков на сирийский язык, а два века спустя появились арабские переводы этих трудов. Так было положено начало ближневосточной математической школе. Большое влияние на неё оказала и индийская математика, также испытавшая сильное древнегреческое влияние. В начале IX века научным центром халифата становится Багдад, где халифы создают «Дом мудрости», в который приглашаются виднейшие учёные всего исламского мира —сабии (потомки вавилонских жрецов-звездопоклонников), тюрки и другие. На западе халифата, в испанской Кордове, сформировался другой научный центр, благодаря которому античные знания стали понемногу возвращаться в Европу. Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, были задачи о расчёте лунного календаря, об определении киблы — точного направления на Мекку.
В целом, эпоха исламской цивилизации в математических науках может быть охарактеризована не как эпоха поиска новых знаний, но — как эпоха передачи и улучшения знаний, полученных от греческих математиков.
§4. Средневековье, IV - XV века
В это время мы можем отметить расцвет математики как науки.
В конце XII века на базе нескольких монастырских школ был создан ^ Возникают Оксфорд и Кембридж в Британии.
Первым крупным математиком средневековья стал Леонардо Пизанский, известный под прозвищем Фибоначчи.
§5. Математика у русского народа
Интерес к науке на Руси появился рано. Сохранились сведения о школах при Владимире Святославовиче и Ярославе Мудром (XI век).
Русский народ создал свою собственную систему мер:
1 миля = 7 верстам ( 7,47 км)
1 верста = 500 саженям ( 1,07 км)
1 сажень = 3 аршинам = 7 футам ( 2,13 м)
1 аршин = 16 вершкам = 28 дюймам ( 71,12 см)
1 фут = 12 дюймам (30,48 см)
1 дюйм = 10 линиям ( 2,54 см)
1 линия = 10 точкам ( 2,54 мм).
Интересно, что на Руси когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см, или о богатырях говорили «Богатырь, косая сажень в плечах», т.е. у такого человека по диагонали от мизинца левой руки до пятки правой ноги почти 2 метра 13 сантиметров.
§ 6. Искусство счета.
Изучив этот материал, мы поняли, что искусство счета развивалось с развитием человечества. На ранних ступенях развития общества люди почти не умели считать. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Это был еще не счет, а лишь его зародыш. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
Впоследствии способность различать друг от друга небольшие совокупности развивалась; появились слова обозначающие числа «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Народные пословицы сохранили память о появлении названий числа 7. К примеру, такие как: «семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ», «семеро одного не ждут» и другие.
Однако когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше семи), заготовленными на зиму. Поэтому счет получил свое дальнейшее развитие.
Способов счета было придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков.
Но палку с зарубками с собой не возьмешь, да и камни таскать не очень приятно, а пастуху нужно знать, не отбилась ли какая коза от стада. И тут на помощь приходят пальцы рук — отличный счетный материал, кстати.
^
Жизнь наших предков была намного проще, но даже они вынуждены были прибегать к использованию числа.
Продолжая изучать литературу по данной теме, мы заметили, что математика - это не только стройная система законов, но и уникальное средство познания красоты. А красота многогранна и многолика.
Рассмотрим применение математики в окружающей нас жизни.
^
§ 1. Математика в мире растений.
Мир растений - величайшее чудо природы, царство красоты и наше целительное богатство. Изучением лекарственных растений занимается наука фитотерапия. Конечно, в этой науке математика играет не последнюю роль. О том, что и здесь применяется математика, мы можем найти сколь угодно много подтверждений. Перелистывая учебник математики, мы с интересом прочитали эту задачу, и хотим её вам представить:
(Приложение 1).
§ 2. Математика в жизни животных и насекомых.
Мир животных и насекомых - богатый и разнообразный мир живых существ. Этот мир, скажете вы, изучает раздел биологии - зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.
Вот, к примеру, пчёлы - удивительное творение природы. Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет (шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.
Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?
Убедиться в том, что математика применяется в изучении жизни животных, мы сможете, решив следующую задачу. (Приложение 2).
§ 3. Математика геометрических тел и фигур.
Тела и фигуры изучает раздел математики, который называется геометрией. Эта наука возникла в Древней Греции исключительно из практических целей, для измерения участков земли. В том, что с фигурами и телами мы имеем дело в жизни, убеждать, думаем, никого не придётся, а вот понять роль математики в этом, Вы сможете, решив следующую задачу (Приложение 3).
§ 4. Математика и культура.
Нам стало интересно, а какое отношение имеет математика к культуре: ведь это и памятники архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать решили с удивительных архитектурных памятников.
Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах - это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.
Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».
Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения примерно )
Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, нежели пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).
Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.
Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».
На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.
Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.
Золотое сечение можно встретить в бытовых предметах и шрифтах.
§ 5. Математика в живой и неживой природе.
Ещё Гете подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно. Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.
Снежинки: ярче примера очаровательной красоты и порядка в природе вы не найдете. Изучением снежинок занимался знаменитый Рене Декарт. А вообще-то, снежинки - это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».
Проанализировав приложение математики в окружающей нас жизни, хочется заметить, что красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность открывать всё новые и новые слагаемые красоты. Так и хочется сказать словами поэта
Все в мире связано в единое начало:
В движенье волн – шекспировский сонет,
В симметрии цветка – основы мирозданья,
А в пенье птиц - симфония планет.
У. Блейк
Изучив весь представленный вам материал, мы поняли, что о математике можно говорить вечно. Наверное, поэтому и символ вечности «∞» (бесконечность) мог появиться только с развитием этой науки «Математика». Мы решили перейти к практической части исследования и для начала провели небольшой социологический опрос, который должен нам помочь подтвердить или опровергнуть выдвинутую ранее гипотезу: если математика второстепенная наука, то законы, которые она изучает знать простому человеку совсем не обязательно, то есть эти законы в обыденной жизни никому не нужны.
^
Прежде чем сделать окончательный вывод, что для нас математика, мы предлагаем изучить результаты социологического опроса.
Цель опроса - изучение общественного мнения по данной теме.
Опрос вёлся по следующим направлениям:
1) математика - это жизнь,
2) нужна ли математика в жизни людей,
3) где находит свое применение математика.
Опрос проводился среди следующих категорий:
1) учащиеся 6А, 11А, 11Б СШ № 2,
2) учителя СШ № 2 (выборочно),
3) родители 6А и 11А, 11Б классов (выборочно)
В опросе приняли участие ___100____ человек.
Вот что у нас получилось:
I направление. Математика - это жизнь
Результаты данного направления говорят о том, что математика является жизнью для 90 человек из числа всех опрошенных, для 8 человек математика - это просто наука, 2 человека затруднялись ответить, что для них математика.
II направление. Нужна ли математика в жизни людей?
Нужна ли математика в жизни людей?
Данная диаграмма показывает, что математика нужна 90% (90 человек из 100) и не нужна 10% (10 человек из 100).
III направление. Где находит свое применение математика?
Ответы на этот вопрос приведены в следующей таблице.
| 17 | |
| 26 |
| 15 |
| 11 | |
| 10 |
| 7 | |
| 9 |
| 5 |
Так отвечали не только дети, но и взрослые.
Заключение
Результаты исследования
Итак, гипотеза, которую мы выдвинули в начале нашего исследования, на практике не подтвердилась. Следовательно, предположение о том, что математика - это второстепенная наука, неверно.
Таким образом, на основании изученной литературы и анализа результатов общественного мнения, мы можем сделать вывод о том, что без знания математики вся современная жизнь невозможна. Например, у нас не было бы хороших домов, т. к. строители должны уметь измерять, считать, сооружать. Наша одежда была бы грубой, т. к. её нужно хорошо скроить. Не было бы ни железных дорог, ни кораблей, ни самолётов, никакой промышленности и тысячи других вещей составляющих часть нашей цивилизации.
В данной работе мы выяснили, математика - часть мира, в котором мы живём.
О мир, пойми! Певцом во сне –
открыты
Закон звезды и формула цветка.
М. Цветаева.
Поэтому мы может с полной и абсолютной уверенностью воскликнуть:
Математика - это жизнь!
Список использованных источников информации
1. За страницами учебника математики. - И. Я. Депман, Н. Я. Виленкин
2. С математикой в путь. - Н. Лэнгдон, Ч. Снейп
3. www.abc-people.com/data/leonardov/zolot_sech-txt.htm - Золотое сечение.
4. http://tmn.fio.ru/works/04x/304/p4_21k.htm - Биология.
5. http://festival.1september.ru/2004_2005/index.php?numb_artic=213063-
История математики.
6. http://bse.sci-lib.com/article048077.html - Золотое сечение.
7. http://www.mjagkov.de/ser/archives/42-,.html
8. http://namangan34.connect.uz/lifemath/links.php - Живая математика
9. Учебник «Математика – 6». – Алдамуратова Т.А., Байшоланов Т.С.,
издательство «Атамұра», 2002 год, 2011 год.
Приложения
Приложение 1. учебник «Математика – 6», изд. «Атамұра», 2011 год.
Задача № 126
Садовник разложил в три ящика яблоки, сливы и груши. Он написал на ящиках: «яблоки», «сливы», «яблоки и груши», но эти надписи не соответствуют тому, что разложено в каждый ящик. В какой ящик, что разложил садовник?
Решение.
1. Из первого ящика с надписью «яблоки» возьмем один фрукт. Если это яблоко, следовательно, с учетом условия задачи здесь яблоки и груши. Тогда яблоки в ящике с надписью «сливы», а сливы - с надписью «яблоки и груши». Если из первого ящика с надписью «яблоки» вынули сливу, тогда с учетом условия задачи, во втором ящике с надписью «слива» находятся яблоки и груши, а в третьем, с надписью «яблоки и груши» - только яблоки.
2. Аналогично можно выбрать один фрукт из ящика с надписью «яблоки и груши» или «сливы» и с учетом условия задачи, определить в какой ящик, какие фрукты разложил садовник.
Приложение 2. учебник «Математика – 6», изд. «Атамұра», 2011 год.
Задача № 747*
Три обезьяны за три минуты съели три банана. Сколько бананов съедят шесть обезьян за четыре минуты?
Решение.
1. 3 : 3 = 1 (банан) – съедает за 3 минуты 1 обезьяна
2. 1 : 3 = 1/3 (часть банана) – съедает 1 обезьяна за 1 минуту
3. 6 · 1 = 6 (бананов) – съедят 6 обезьян за 3 минуты
4. 6 · 1/3 = 2 (банана) – съедят 6 обезьян за 1 минуту
5. 6 + 2 = 8 (бананов) – съедят 6 обезьян за 4 минуты
Ответ: 8 бананов.
Приложение 3. учебник «Математика – 6», изд. «Атамұра», 2002 год
Задача № 1143. Найти площадь фигуры, вершинами которой будут точки: А(-3;3), В(5;3), С(5;-2) и D(-3;-2) на координатной плоскости. Пусть единичный отрезок будет равен 1 см.
Решение.
Построим на координатной плоскости фигуру АВСD, зная координаты её вершин. Данная фигура является прямоугольником, что мы видим по построению. Чтобы вычислить площадь прямоугольника АВСD нам нужно знать размеры длины и ширины.
Посчитаем, сколько единичных отрезков содержат длина и ширина данного прямоугольника, и учтем, что по условию единичный отрезок будет равен 1 см,
получим: АВ=8(ед.отр.)=8см, ВС=5(ед.отр.)=5см.
Вычислим площадь прямоугольника АВСD по формуле:
S=а·в, S=8·5=40 (см²).
Можно было упростить решение задачи. Учитывая, что фигура задана на координатной плоскости, посчитаем количество квадратиков (как на палетке). Получаем площадь прямоугольника АВСD равна 40 квадратиков (площадь каждого квадратика равна 1).
Ответ: площадь прямоугольника равна 40 см².
В(5;3)А(-3;3)
С(5;-3)
D(-3;-2)
Х
У
Отзыв
На научно-исследовательскую работу Хабибулиной Регины и Смирновой Екатерины учениц 6-А класса.
Данная исследовательская работа выполнена по теме: «Математика это жизнь», проблемно-поисковая.
Работа выполнена на 23 листах. В ходе выполнения работы авторы использовали дополнительную литературу, интернет-ресурсы, провели опрос учащихся трех классов, учителей школы и родителей двух классов (выборочно). Данная работа является теоретической, исследовательской, проблемно-поисковая. Авторы изучили много дополнительной литературы, чтобы опровергнуть гипотезу о том, что математика - это второстепенная наука. На основании изученной литературы и анализа результатов общественного мнения, они сделали вывод о том, что без знания математики вся современная жизнь невозможна. В ходе работы над темой, изучив приложение математики в природе, искусстве, архитектуре, культуре, выяснили, что математика - часть мира. Над данной темой авторы проработали в течение шести месяцев, подготовили презентацию к своей работе. Подготовленный ими материал можно использовать на уроках математики, на занятиях кружка.
Учитель математики
высшей категории Хабибулина Л.В.
dmee.ru
"Мир красоты математики" - Математика

Математика владеет не только истиной, но и высшей красотой.
В математике есть своя красота, как в живописи и поэзии.
(Н.Е. Жуковский)
Автор: учитель физики и информатики Александрова З.В.,
МОУ СОШ №5 п.Печенга, Мурманская обл., 2010 г.

Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства.
Это не только стройная система законов, но и уникальное средство познания красоты.
«Математика есть прообраз красоты мира»
(В.Гейзенберг)

Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем.
В жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач.
Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею.

Математическая пирамида №1
1 x 8 + 1 = 9 12 x 8 + 2 = 9 8 123 x 8 + 3 = 9 8 7 1234 x 8 + 4 = 9 8 7 6 12345 x 8 + 5 = 9 8 7 6 5 123456 x 8 + 6 = 9 8 7 6 5 4 1234567 x 8 + 7 = 9 8 7 6 5 4 3 12345678 x 8 + 8 = 9 8 7 6 5 4 3 2 123456789 x 8 + 9 = 9 8 7 6 5 4 3 2 1
Какие вычисления будут выполнены в следующей строке и в последующих?
Математика - это красота и чудо в чистом виде.
4

Математическая пирамида №2
1 x 9 + 2 = 11 12 x 9 + 3 = 111 123 x 9 + 4 = 1111 1234 x 9 + 5 = 11111 12345 x 9 + 6 = 111111 123456 x 9 + 7 = 1111111 1234567 x 9 + 8 = 11111111 12345678 x 9 + 9 = 111111111 123456789 x 9 +10= 1111111111
Какие вычисления будут выполнены в следующей строке и в последующих?
Математика - это единственная наука, которая имеет дело с абсолютным идеалом.

Математическая пирамида №3
9 x 9 + 7 = 88 98 x 9 + 6 = 888 987 x 9 + 5 = 8888 9876 x 9 + 4 = 88888 98765 x 9 + 3 = 888888 987654 x 9 + 2 = 8888888 9876543 x 9 + 1 = 88888888 98765432 x 9 + 0 = 888888888
Какие вычисления будут выполнены в следующей строке и в последующих?
Замечательно! Не правда ли?
6

Математическая пирамида №4
1 x 1 = 1 11 x 11 = 121 111 x 111 = 1 2 3 2 1 1111 x 1111 = 1 23 4 32 1 11111 x 11111 = 1 234 5 432 1 111111 x 111111 = 1 2345 6 5432 1 1111111 x 1111111 = 1 23456 7 65432 1 11111111 x 11111111 = 1 234567 8 765432 1 111111111 x 111111111 = 1 2345678 9 8765432 1
Какие вычисления будут выполнены в следующей строке и в последующих?
Математика в своей сущности достаточно таинственна и романтична.

Это интересно

Поверхности второго порядка. Загадочная красота.
эллипсоид
гиперболический параболоид
эллиптический параболоид
двуполостный гиперболоид

Симметрия - закономерное расположение элементов формы относительно плоскости, оси или точки. Человек давно осмыслил симметрию в творениях природы и стал использовать се как средство организации искусственных форм. В Древней Греции слово "симметрия" было синонимом красоты, гармонии формы.
«...быть прекрасным значит быть симметричным и соразмерным» (Платон)

Тадж-Махал — мавзолей-мечеть, находящийся в Агре, Индия, на берегу реки Ямуна. Усыпальница имеет центральную симметрию относительно гробницы Мумтаз-Махал. Единственным нарушением этой симметрии является гробница Шах-Джахана, которую там соорудили после его смерти.

Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. Древнегреческие архитекторы были убеждены, что в своих произведениях они руководствуются законами, которые управляют природой. Выбирая симметричные формы, художник тем самым выражал свое понимание природной гармонии как устойчивости, спокойствия и равновесия.

Зеркальная симметрия
Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры. В некоторых источниках такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние и задние по отношению к зеркалу части объекта.

Симметрия в природе
Симметрия широко распространена в природе. Ее можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных.

Симметрия в природе
Красота растений привлекала внимание математиков веками. Активнее всего изучались интересные геометрические свойства растений, такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. Красота связана с симметрией .
Рассматривая расположение листьев на ветке дерева, видим, что один лист не только отстоит от другого , но и повёрнут вокруг оси ствола. Листья располагаются на стволе по винтовой линии (принцип винтовой симметрии). Семена подсолнечника располагаются по спиралям, опять же по принципу симметрии.

Симметрия в неживой природе
В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.

О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений.

Аристид Линденмайер
В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов.

R ewriting
R ewriting — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является снежинка. На рисунке initiator — это начальный объект, грани которого заменяются на generator. Далее с новым объектом проделывается то же самое.

Замощение Пенроуза
Его красота в непериодичности. Любой сколь угодно большой фрагмент узора повторяется бесконечное число раз, однако, нет таких двух точек где узор наложился бы сам на себя полностью (как не крути).

Дерево Пифагора
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево.
Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время второй мировой войны, используя обычную чертёжную линейку.
Одним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.

Обнаженное дерево Пифагора
Классическое дерево Пифагора
Если изображать только отрезки, соединяющие каким-либо образом выбранные "центры" треугольников, то получается обнаженное дерево Пифагора.

Обдуваемое ветром дерево Пифагора
Если в классическом дереве Пифагора угол равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора.

Гипножаба
24

История
Красота есть истина, а истина — красота.
Джон Китс
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы». Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому"

Галерея изображений фракталов
Они кажутся более живыми и красивыми, чем многие рисунки, несмотря на то, что являются результатом работы программы.

Математическая музыка
Пифагор создал свою школу мудрости, положив в ее основу два искусства - музыку и математику. Он считал, что гармония чисел сродни гармонии звуков и что оба этих занятия упорядочивают хаотичность мышления и дополняют друг друга. Пифагор говорил своим ученикам, что числа правят миром.
Математика и музыка - два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом.
Дроби широко используются в музыке для обозначения длительностей нот.

Золотое сечение
Средневековая математика подарила нам понятие о "золотом сечении" и последовательности Фибоначчи.
Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.
Эта последовательность имеет следующий вид: 1,1,2,3,5,8,13,21,...
То есть каждое последующее число равно сумме двух предыдущих. При этом в пределе деление каждого числа на предыдущее даёт приблизительно 1,618 - это число и определяет "золотое сечение".

Золотое сечение
"Золотое сечение" в конструкции Парфенона, Афины, Греция
Собор "Нотредам де Пари" в Париже, Франция
Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Пирамида Хеопса, Египет

Пропорции Фибоначчи в природе
Еще Гете подчеркивал тенденцию природы к спиральности. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль "кривой жизни".

Золотое сечение
В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Золотое сечение в живописи
33

Золотое сечение
Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности есть в строении отдельных органов человека и тела в целом.

Математик так же, как художник или поэт, создаёт узоры…
В математике есть тоже своя красота, как в живописи и поэзии. Эта красота проявляется иногда в отчетливых, ярко очертанных идеях, где на виду всякая деталь умозаключения, а иногда поражает она нас в широких замыслах, скрывающих в себе кое-что недосказанное, но многообещающее. (Н.Е. Жуковский )

Автор: учитель физики и информатики Александрова З.В.,
МОУ СОШ №5 п.Печенга, Мурманская обл., 2010 г.
Спасибо за внимание!
Использованные ресурсы:
http://mcs.open.ac.uk/ugg2/jpg/med_RS_0065.jpg
http://en.wikipedia.org/wiki/Penrose_tiling
http://habrahabr.ru/blogs/biotech/69989
http://ru.wikipedia.org/wiki/ Фрактал
http://fractals.narod.ru/intro.htm
http://www.wack.ch/frac/gallery.html
http://www.ug.ru/issue/?action=topic&toid=8652
http://www.mathematics.ru/
«Математика и искусство», А. В. Волошинов, Москва, “Просвещение”, 2000г.
«Математическое путешествие в мир гармонии», Е.С.Смирнова, Н.А. Леонидова, журнал «Математика в школе» № 3, 1993г.
multiurok.ru
"Математика-это жизнь" ученика 5 класса.
Проект
Тема: «Математика - это жизнь»

Автор: Загнухин Никита.
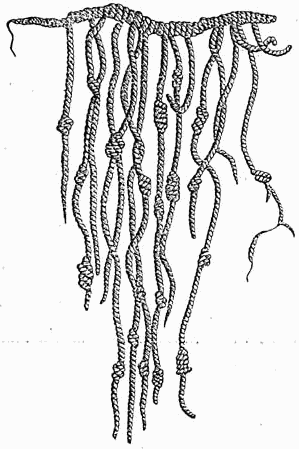 Ученик 5 класса
Ученик 5 класса
У

2016 учебный год
МОУ Краснореченская ср. школа
Учитель:Кирилова Н.Ф.
Оглавление
Отзыв о работе.
2. Введение (цель, задачи, гипотеза, методы исследования)
3. Теоретическая часть:
Вступление.
Глава I. Из истории возникновения математики.
§ 1. Возникновение арифметики и теории чисел.
§ 2. Античная математика.
§ 3. Страны ислама.
§ 4. Математика средневековья: IV-XV века.
§ 5. Математика на Руси.
§ 6. Искусство счета.
Глава II. Применение математики в окружающей нас жизни.
§ 1. Математика в мире растений.
§ 2. Математика в жизни животных.
§ 3. Математика геометрических тел и фигур.
§ 4. Математика и культура.
§ 5. Математика в живой и неживой природе.
4. Практическая часть
5. Заключение
6. Список использованных источников информации
7. Приложения
Введение
Данная работа относится к разделу проблемно - исследовательскому.
Цель работы: выяснить, что значит математика в жизни людей: является второстепенной наукой или математика – это неотъемлемая часть в жизни человечества.
Задачи работы:
1) рассмотреть взаимосвязь между математикой и жизнью,2) проанализировать, как жизнь зависит от математики.
Гипотеза: если математика - второстепенная наука, то законы, которые она изучает знать простому человеку совсем не обязательно, то есть эти законы в обыденной жизни никому не нужны.
Практическая значимость: если гипотеза подтверждается, то можно утверждать, что без математики можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.
Методы исследования:подбор задач, подтверждающих связь математики с жизнью;
Теоретическая часть
Вступление.
Так, изучив в 5-м классе простые и составные числа, нам стало интересно, а есть ли число, которое больше вселенной? Ведь при этом нужно учитывать тот факт, что каждое следующее число больше предыдущего хотя бы на единицу. Оказалось очень трудным делом найти самое большое число. Такие числа оказалось для нас не только трудно прочитать, но и записать. А как же с такими числами, спросите Вы, можно выполнять арифметические действия? Ну конечно, ответят им многие, ведь современные компьютеры достигли потрясающих скоростей быстродействия. Поэтому некоторым, кажется, что в современном мире все можно просчитать, достаточно только взять компьютер помощнее. Но это не так.
Ведь до сих пор в мире нет признанной всеми системы наименований больших и сверхбольших чисел. А в словарях, кроме центиллиона, нет названий для чисел, имеющих порядок больше 63 (такое число называют вигинтиллионом).
Свою систему наименований для чисел предлагал Архимед. С ее помощью он мог именовать числа вплоть до 1080000000000000000, которое он называл «последним числом».
Изучив это, мы убедились в том, что попытка найти самое большое число приводит нас в тупик, так как к любому числу достаточно всего лишь прибавить единицу, чтобы получить число большее данного.
Из всего этого мы поняли, что человека окружает громадное количество фактов и явлений, которые в силу своей огромности кажутся далекими и недоступными пониманию, но при глубоком изучении становятся близкими, интересными, загадочными.… И тут нас осенило.
Эврика! Все в мире и в жизни тесно связано с математикой! Вот и нашлась прекрасная тема для проекта: «Математика в жизни людей», или «Математика – это жизнь»
Мы специально не ставим никакого знака препинания в конце предложения, так как считаем, что эту фразу можно произнести с разной интонацией: кто–то её произнесет вопросительно, кто–то с восклицанием, а кто–то просто повествовательно.
В своей работе мы попытаемся выяснить, так что же для нас математика? Может быть, это жизнь, а может быть, это просто наука, которая является для нас второстепенной и заниматься ею нужно только ученым?
Своё исследование мы решили начать с изучения истории математики.
Глава I. Из истории возникновения математики.
§ 1. Возникновение арифметики и теории чисел.
Учёные - археологи обнаружили стойбище древних людей. В нём они нашли волчью кость, на которой 30 тысяч лет назад какой - то древний охотник нанёс 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам.
Много тысячелетий прошло с тех пор. Но и сейчас швейцарские крестьяне, отправляя молоко на сыроварню, отмечают число фляг такими, же зарубками. До сих пор в русском языке сохранилось слово «бирка». Теперь так называют дощечку с номером, которой отмечают товар. А ещё 200 - 300 лет тому назад так называли куски дерева, на которых зарубками отмечали сумму долга. Бирку с зарубками раскалывали пополам. При расчёте половинки складывались вместе, и это позволяло определить сумму долга без споров и сложных вычислений.
Первыми понятиями математики, с которыми столкнулись люди, были «меньше», «больше», «столько же». Если одно племя меняло рыбу на сделанные другим племенем каменные ножи, достаточно было положить рядом с каждой рыбой один нож, соответствующий величине рыбы, чтобы сделка состоялась.
А вот так выглядело счётное устройство инков, которое состояло из узелков, завязанных на веревках разной длины. Если внимательно приглядеться, то эти узелки чем-то отдаленно напоминают счеты.

Для запоминания результатов счёта использовали зарубки, узелки и т. п.
Были и более экзотичные варианты. Например, такие математические таблицы древних, обнаружены на территории современной Армении.
Одна из древнейших нумераций, дошедших до нас в древних папирусах и рисунках, была – египетская.

Для записи чисел египтяне использовали картинки-иероглифы, означавшие буквально следующее:
 - собственно 1.
- собственно 1.  - 10.
- 10.  - 100.
- 100.  - 1 000.
- 1 000.  - 10 000.
- 10 000.  - 100 000.
- 100 000.  - 1 000 000.
- 1 000 000.  - 10 000 000.
- 10 000 000.
К примеру, число 2253 на этой картинке было изображено так:

- две тысячи, две сотни, пять десятков и три единицы.
Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта и подчинении его власти Александра Македонского.
Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел. Недаром ведь говорят: «Без названия нет знания».
О том, как появились имена у чисел, учёные узнают, изучая языки разных народов и племён. Ведь, как известно, учёные считают, что сначала названия получили числа 1 и 2.
Когда римляне (в древности они говорили на латыни) придумывали имя числу 1(солюс), они исходили из того, что Солнце на небе одно. А название для числа 2 во многих языках связано с предметами, встречающимися попарно, - крыльями, ушами, руками и т.д.
А есть более экзотичные варианты.
Например, на языке некоторых папуасских племён (о. Новая Гвинея) числа назвали так: 1 - «урапун», 2 - «оказа», 3 - «оказа -урапун», 4 - «оказа - оказа», 5 - «оказа - оказа - урапун», 6 - «оказа - оказа - оказа» и «много», как самое большое число. Правда, интересно! Но тогда как, же считать такими числами расстояния до звезд, размеры галактики, или как этими числами папуасские племена обозначали бы мельчайшие размеры атома?!
§ 2. Античная математика.
Третий век до нашей эры был золотым веком античной математики.
В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию.
В III веке до н. э. в городе Александрия Птолемей I основал Дом Муз и пригласил туда виднейших учёных. Это была первая академии, с богатейшей библиотекой, которая к I веку до н. э. насчитывала 70000 книг.
Но самая громкая слава выпала на долю трёх великих геометров античной математики – это, конечно же, Евклид, Архимед и Апполоний Пергский. Евклид (написал книгу «Начала», авторитет которой был и остается огромным более 2000 лет), Архимед (развил метод вычисления площадей и объёмов геометрических фигур и тел), Аполлоний Пергский (автор исследования сечений геометрических тел).
А такие два достижения греческой математики далеко пережили своих творцов.
1) греки построили и представили миру математику как целостную науку;
2) греки провозгласили, что законы природы постижимы для человеческого разума.
§3. Страны ислама
Математика Востока, в отличие от греческой, всегда носила более практический характер. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика. Преследование греческих учёных-нехристиан в Римской империи V—VI веков вызвало их массовое бегство на восток, в Персию и Индию. При дворе Хосрова I они переводили античных классиков на сирийский язык, а два века спустя появились арабские переводы этих трудов. Так было положено начало ближневосточной математической школе. Большое влияние на неё оказала и индийская математика, также испытавшая сильное древнегреческое влияние. В начале IX века научным центром халифата становится Багдад, где халифы создают «Дом мудрости», в который приглашаются виднейшие учёные всего исламского мира —сабии (потомки вавилонских жрецов-звездопоклонников), тюрки и другие. На западе халифата, в испанской Кордове, сформировался другой научный центр, благодаря которому античные знания стали понемногу возвращаться в Европу. Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, были задачи о расчёте лунного календаря, об определении киблы — точного направления на Мекку.
В целом, эпоха исламской цивилизации в математических науках может быть охарактеризована не как эпоха поиска новых знаний, но — как эпоха передачи и улучшения знаний, полученных от греческих математиков.
§4. Средневековье, IV - XV века
В это время мы можем отметить расцвет математики как науки.
В конце XII века на базе нескольких монастырских школ был создан Парижский университет. Возникают Оксфорд и Кембридж в Британии.
Первым крупным математиком средневековья стал Леонардо Пизанский, известный под прозвищем Фибоначчи.
§5. Математика у русского народа
Интерес к науке на Руси появился рано. Сохранились сведения о школах при Владимире Святославовиче и Ярославе Мудром (XI век).
Русский народ создал свою собственную систему мер:
1 миля = 7 верстам ( 7,47 км)
7,47 км)
1 верста = 500 саженям ( 1,07 км)
1,07 км)
1 сажень = 3 аршинам = 7 футам ( 2,13 м)
2,13 м)
1 аршин = 16 вершкам = 28 дюймам ( 71,12 см)
71,12 см)
1 фут = 12 дюймам ( 30,48 см)
30,48 см)
1 дюйм = 10 линиям ( 2,54 см)
2,54 см)
1 линия = 10 точкам ( 2,54 мм).
2,54 мм).
Интересно, что на Руси когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см, или о богатырях говорили «Богатырь, косая сажень в плечах», т.е. у такого человека по диагонали от мизинца левой руки до пятки правой ноги почти 2 метра 13 сантиметров.
§ 6. Искусство счета.
Изучив этот материал, мы поняли, что искусство счета развивалось с развитием человечества. На ранних ступенях развития общества люди почти не умели считать. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Это был еще не счет, а лишь его зародыш. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
Впоследствии способность различать друг от друга небольшие совокупности развивалась; появились слова обозначающие числа «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Народные пословицы сохранили память о появлении названий числа 7. К примеру, такие как: «семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ», «семеро одного не ждут» и другие.
Однако когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше семи), заготовленными на зиму. Поэтому счет получил свое дальнейшее развитие.
Способов счета было придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков.
Но палку с зарубками с собой не возьмешь, да и камни таскать не очень приятно, а пастуху нужно знать, не отбилась ли какая коза от стада. И тут на помощь приходят пальцы рук — отличный счетный материал, кстати.
Таким образом, можно сделать первый вывод: древний человек хотел учитывать вещи, которыми он владел. Сколько у него инструментов? Сколько оружия? Сколько животных?
Жизнь наших предков была намного проще, но даже они вынуждены были прибегать к использованию числа.
Продолжая изучать литературу по данной теме, мы заметили, что математика - это не только стройная система законов, но и уникальное средство познания красоты. А красота многогранна и многолика.
Рассмотрим применение математики в окружающей нас жизни.
Глава II. Применение математики в окружающей нас жизни.
§ 1. Математика в мире растений.
Мир растений - величайшее чудо природы, царство красоты и наше целительное богатство. Изучением лекарственных растений занимается наука фитотерапия. Конечно, в этой науке математика играет не последнюю роль. О том, что и здесь применяется математика, мы можем найти сколь угодно много подтверждений. Перелистывая учебник математики, мы с интересом прочитали эту задачу, и хотим её вам представить:
(Приложение 1).
§ 2. Математика в жизни животных и насекомых.
Мир животных и насекомых - богатый и разнообразный мир живых существ. Этот мир, скажете вы, изучает раздел биологии - зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.



Вот, к примеру, пчёлы - удивительное творение природы. Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет (шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.
Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?





Убедиться в том, что математика применяется в изучении жизни животных, мы сможете, решив следующую задачу. (Приложение 2).
§ 3. Математика геометрических тел и фигур.



Тела и фигуры изучает раздел математики, который называется геометрией. Эта наука возникла в Древней Греции исключительно из практических целей, для измерения участков земли. В том, что с фигурами и телами мы имеем дело в жизни, убеждать, думаем, никого не придётся, а вот понять роль математики в этом, Вы сможете, решив следующую задачу (Приложение 3).
§ 4. Математика и культура.
Нам стало интересно, а какое отношение имеет математика к культуре: ведь это и памятники архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать решили с удивительных архитектурных памятников.
Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах - это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.
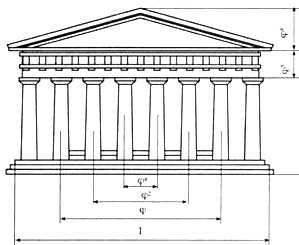

Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».
Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.



Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения примерно 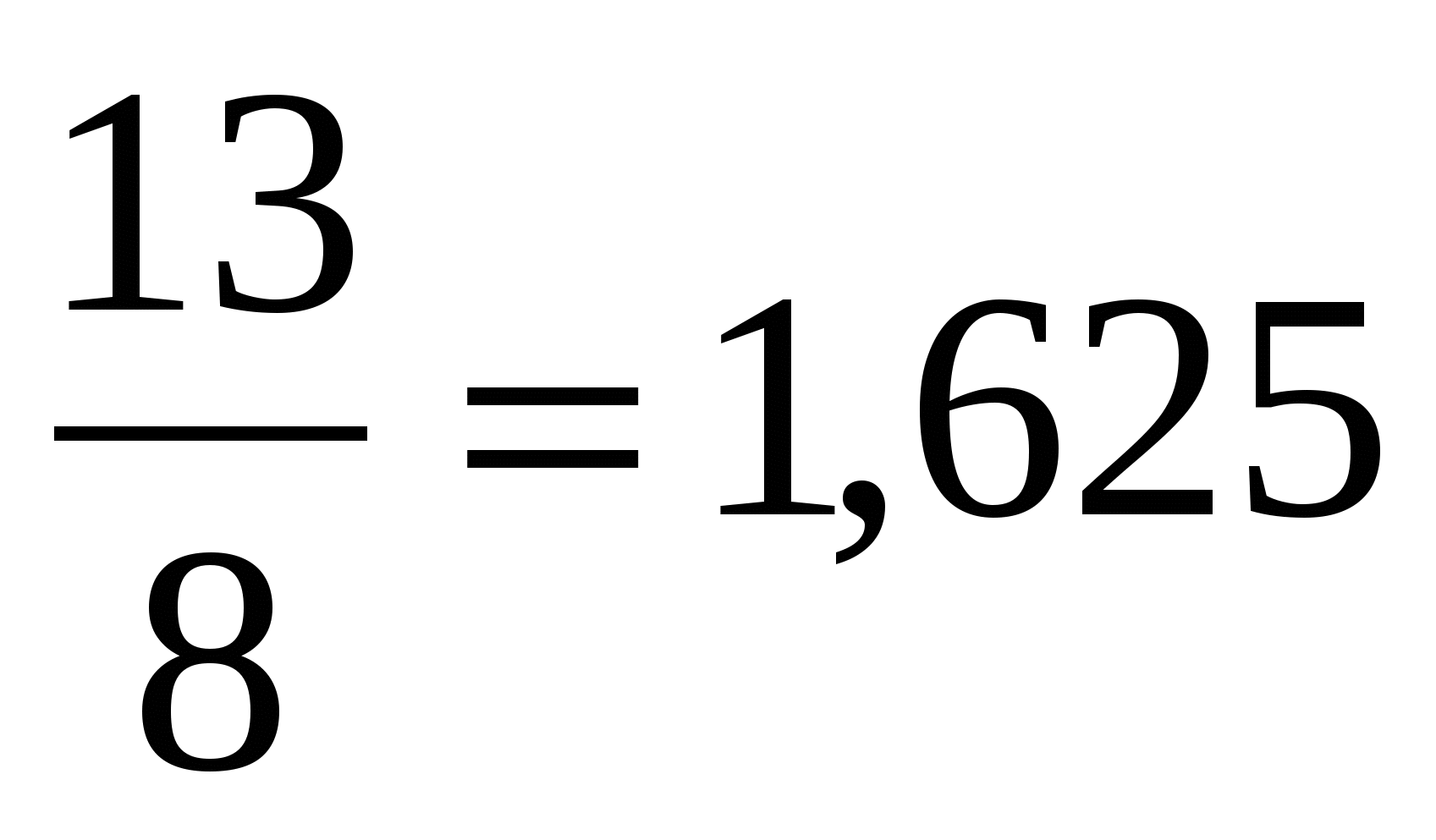 )
) 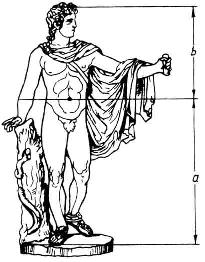
Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, нежели пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).
Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.
Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».

На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.

Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.
Золотое сечение можно встретить в бытовых предметах и шрифтах.
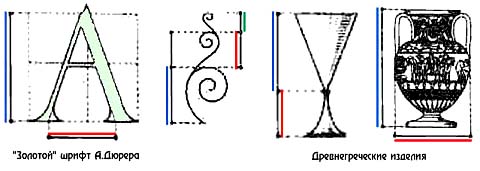
§ 5. Математика в живой и неживой природе.
Ещё Гете подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно. Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.



Снежинки: ярче примера очаровательной красоты и порядка в природе вы не найдете. Изучением снежинок занимался знаменитый Рене Декарт. А вообще-то, снежинки - это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».




Проанализировав приложение математики в окружающей нас жизни, хочется заметить, что красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность открывать всё новые и новые слагаемые красоты. Так и хочется сказать словами поэта
Все в мире связано в единое начало:
В движенье волн – шекспировский сонет,
В симметрии цветка – основы мирозданья,
А в пенье птиц - симфония планет.
У. Блейк
Изучив весь представленный вам материал, мы поняли, что о математике можно говорить вечно. Наверное, поэтому и символ вечности «∞» (бесконечность) мог появиться только с развитием этой науки «Математика». Мы решили перейти к практической части исследования и для начала провели небольшой социологический опрос, который должен нам помочь подтвердить или опровергнуть выдвинутую ранее гипотезу: если математика второстепенная наука, то законы, которые она изучает знать простому человеку совсем не обязательно, то есть эти законы в обыденной жизни никому не нужны.
Практическая часть
Прежде чем сделать окончательный вывод, что для нас математика, мы предлагаем изучить результаты социологического опроса.
Цель опроса - изучение общественного мнения по данной теме.
Опрос вёлся по следующим направлениям:
1) математика - это жизнь,
2) нужна ли математика в жизни людей,
3) где находит свое применение математика.
Опрос проводился среди следующих категорий:
1) учащиеся 5кл
В опросе приняли участие 12 человек.


Результаты данного направления говорят о том
, что математика является жизнью для 10 человек из числа всех опрошенных, для 1человек математика - это просто наука, 1человек
з
Нужна ли математика в жизни людей?
атруднялся ответить.
 Нужна ли математика в жизни
Нужна ли математика в жизни 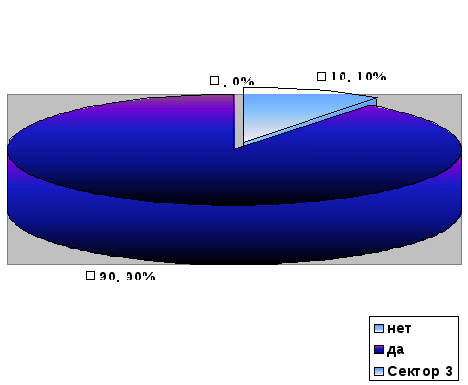

Д



 анная диаграмма показывает, что математика нужна 90% и не нужна 10%
анная диаграмма показывает, что математика нужна 90% и не нужна 10%
III направление. Где находит свое применение математика?
Ответы на этот вопрос приведены в следующей таблице.
1
9
1
1
всего: 12человек
Заключение
Результаты исследования
Итак, гипотеза, которую мы выдвинули в начале нашего исследования, на практике не подтвердилась. Следовательно, предположение о том, что математика - это второстепенная наука, неверно.
Таким образом, на основании изученной литературы и анализа результатов общественного мнения, мы можем сделать вывод о том, что без знания математики вся современная жизнь невозможна. Например, у нас не было бы хороших домов, т. к. строители должны уметь измерять, считать, сооружать. Наша одежда была бы грубой, т. к. её нужно хорошо скроить. Не было бы ни железных дорог, ни кораблей, ни самолётов, никакой промышленности и тысячи других вещей составляющих часть нашей цивилизации.
В данной работе мы выяснили, математика - часть мира, в котором мы живём.
О мир, пойми! Певцом во сне –
открыты
Закон звезды и формула цветка.
М. Цветаева.
Поэтому мы может с полной и абсолютной уверенностью воскликнуть:
Математика - это жизнь!
Список использованных источников информации:
1. За страницами учебника математики. - И. Я. Депман, Н. Я. Виленкин
2. С математикой в путь. - Н. Лэнгдон, Ч. Снейп
3. www.abc-people.com/data/leonardov/zolot_sech-txt.htm - Золотое сечение.
4. http://tmn.fio.ru/works/04x/304/p4_21k.htm - Биология.
5. http://festival.1september.ru/2004_2005/index.php?numb_artic=213063-
История математики.
1.
Садовник разложил в три ящика яблоки, сливы и груши. Он написал на ящиках: «яблоки», «сливы», «яблоки и груши», но эти надписи не соответствуют тому, что разложено в каждый ящик. В какой ящик, что разложил садовник?
Решение.
1. Из первого ящика с надписью «яблоки» возьмем один фрукт. Если это яблоко, следовательно, с учетом условия задачи здесь яблоки и груши. Тогда яблоки в ящике с надписью «сливы», а сливы - с надписью «яблоки и груши». Если из первого ящика с надписью «яблоки» вынули сливу, тогда с учетом условия задачи, во втором ящике с надписью «слива» находятся яблоки и груши, а в третьем, с надписью «яблоки и груши» - только яблоки.
2. Аналогично можно выбрать один фрукт из ящика с надписью «яблоки и груши» или «сливы» и с учетом условия задачи, определить в какой ящик, какие фрукты разложил садовник
2.
Три обезьяны за три минуты съели три банана. Сколько бананов съедят шесть обезьян за четыре минуты?
Решение.
1. 3 : 3 = 1 (банан) – съедает за 3 минуты 1 обезьяна
2. 1 : 3 = 1/3 (часть банана) – съедает 1 обезьяна за 1 минуту
3. 6 · 1 = 6 (бананов) – съедят 6 обезьян за 3 минуты
4. 6 · 1/3 = 2 (банана) – съедят 6 обезьян за 1 минуту
5. 6 + 2 = 8 (бананов) – съедят 6 обезьян за 4 минуты
Ответ: 8 бананов.
3.Задача № 1143. Найти площадь фигуры, вершинами которой будут точки: А(-3;3), В(5;3), С(5;-2) и D(-3;-2) на координатной плоскости. Пусть единичный отрезок будет равен 1 см.
Решение.
Построим на координатной плоскости фигуру АВСD, зная координаты её вершин. Данная фигура является прямоугольником, что мы видим по построению. Чтобы вычислить площадь прямоугольника АВСD нам нужно знать размеры длины и ширины.
Посчитаем, сколько единичных отрезков содержат длина и ширина данного прямоугольника, и учтем, что по условию единичный отрезок будет равен 1 см,
получим: АВ=8(ед.отр.)=8см, ВС=5(ед.отр.)=5см.
Вычислим площадь прямоугольника АВСD по формуле:
S=а·в, S=8·5=40 (см²).
Можно было упростить решение задачи. Учитывая, что фигура задана на координатной плоскости, посчитаем количество квадратиков (как на палетке). Получаем площадь прямоугольника АВСD равна 40 квадратиков (площадь каждого квадратика равна 1).
Ответ: площадь прямоугольника равна 40 см².

В(5;3)


А(-3;3)
С(5;-3)
D(-3;-2)
Х
У
Отзыв
.
Данная работа является теоретической, исследовательской, проблемно-поисковая. Автор изучил много дополнительной литературы, чтобы опровергнуть гипотезу о том, что математика - это второстепенная наука. На основании изученной литературы он сделал вывод о том, что без знания математики вся современная жизнь невозможна. В ходе работы над темой, изучив приложение математики в природе, искусстве, архитектуре, культуре, выяснили, что математика - часть мира. Подготовленный им материал можно использовать на уроках математики, на занятиях кружка.
Учитель математики:Кирилова Н.Ф.



infourok.ru
Проектная работа "Математика - это красота"
Муниципальное бюджетное общеобразовательное учреждение
Шиковская средняя школа Павловского района Ульяновской области
Научный проект
Тема: «Математика - это красота»

Авторы:
Палей Анастасия,
Мальцев Кирилл,
ученики 6 класса
Секция: математика
Руководитель:
КрестининаВ.П.
2017-2018 учебный год
Оглавление
1. Введение (цель, задачи, гипотеза, методы исследования)
2. Теоретическая часть:
Вступление.
Глава I. Из истории возникновения математики и её взаимосвязи с категорией «красота».
§ 1. Красота в древней арифметике и теории чисел.
§ 2. Античная математика и красота.
§ 3. Страны ислама.
§ 4. Математика средневековья: IV-XV века.
§ 5. Математика на Руси.
§ 6. Искусство счета.
Глава II. Применение законов математики как законов красоты в окружающей нас жизни.
§ 1. Математика в мире растений.
§ 2. Математика в жизни животных.
§ 3. Математика геометрических тел и фигур.
§ 4. Математика и культура.
§ 5. Математика в живой и неживой природе.
3. Практическая часть
4. Заключение
5. Список использованных источников информации
Введение
Данная работа относится к разделу проблемно – исследовательских работ.
Цель работы: выяснить, как соотносятся два понятия: «математика» и «красота». Применима ли математика в жизни людей как наука о красоте или математика и красота это абсолютно различные категории.
Задачи работы:
1) рассмотреть взаимосвязь между математикой, жизнью и категорией «красота».
2) проанализировать, как жизнь зависит от математической основы понятия «красота».
Гипотеза: если понятия «математика» и «красота» абсолютно не взаимосвязаны, то математические законы не влияют на каноны красоты и не востребованы в жизни: в искусстве, в строительстве, дизайне, архитектуре и многих других областях жизнедеятельности человека.
Практическая значимость: если гипотеза подтверждается, то можно утверждать, что без математических законов красоты можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.
Методы исследования:
изучение и анализ литературы по данной теме;
подбор примеров, подтверждающих связь математики с жизнью и категорией «красота»;
сбор и анализ общественного мнения.
Теоретическая часть
Вступление.
На факультативах, готовясь к олимпиаде по математике, мы встретили задачи на золотое сечение. И нам стало интересно узнать про взаимосвязь математики и красоты; есть ли другие примеры зависимости категории «красота» от математических законов; узнать историю применения математики в искусстве и архитектуре и других областях жизни человека.
Чтобы ответить на эти вопросы, мы обратились к книгам и к более современному помощнику по имени «Интернет». В них мы нашли много интересного материала и поняли, что человека окружает громадное количество фактов и явлений, которые в силу своей огромности кажутся хаотичными, далекими и недоступными пониманию, но при глубоком изучении становятся близкими, интересными, загадочными.
Все в мире и в жизни тесно связано с математикой и всё стремится соответствовать понятию «красота»! Вот и нашлась интересная тема для проекта: «Математика – это красота».
В своей работе мы попытаемся выяснить, как же математика связана с красотой? Может быть, математические законы красоты это законы жизни, а может быть, это просто наука, которая является для нас второстепенной и заниматься ею нужно только ученым?
Своё исследование мы решили начать с изучения истории математики.
Глава I. Из истории возникновения математики и её взаимосвязи с категорией «красота».
§ 1. Возникновение арифметики и теории чисел.
Учёные - археологи при раскопках в Египте обнаружили математические записи на папирусах. Много тысячелетий прошло с тех пор.
Одна из древнейших нумераций, дошедших до нас в древних папирусах и рисунках, была – египетская.

Для записи чисел египтяне использовали картинки-иероглифы, означавшие буквально следующее:
 - собственно 1.
- собственно 1.  - 10.
- 10.  - 100.
- 100.  - 1 000.
- 1 000.  - 10 000.
- 10 000.  - 100 000.
- 100 000.  - 1 000 000.
- 1 000 000.  - 10 000 000.
- 10 000 000.
К примеру, число 2253 на этой картинке было изображено так:

- две тысячи, две сотни, пять десятков и три единицы.
Можно отметить, что знаки, обозначающие числа, расположены не хаотично, а упорядоченно, в стройной системе, подчиняясь законам симметрии, стройности, а значит, и красоты.
Как писать, так и считать тогда умели только специально обученные люди, для простых людей счет был так же недоступен, как и письменность. Эта система применялась в Древнем Египте при торговле и сборе податей, особенно распространившись при постройке Великих Пирамид, и постепенно угасла вместе с кастой строителей и счетоводов, при упадке Египта и подчинении его власти Александра Македонского.
Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел. Недаром ведь говорят: «Без названия нет знания».
О том, как появились имена у чисел, учёные узнают, изучая языки разных народов и племён. Ведь, как известно, учёные считают, что сначала названия получили числа 1 и 2.
Когда римляне (в древности они говорили на латыни) придумывали имя числу 1(солюс), они исходили из того, что Солнце на небе одно. А название для числа 2 во многих языках связано с предметами, встречающимися попарно, - крыльями, ушами, руками и т.д.То есть, римляне исходили из соображений целесообразности, опираясь на природные явления и объекты. Вольно или невольно, но получалось точно и красиво.
§ 2. Античная математика.
Третий век до нашей эры был золотым веком античной математики.
В 389 году до н. э. Платон основывает в Афинах свою школу - знаменитую Академию.
В III веке до н. э. в городе Александрия Птолемей I основал Дом Муз и пригласил туда виднейших учёных. Это была первая академии, с богатейшей библиотекой, которая к I веку до н. э. насчитывала 70000 книг.
Но самая громкая слава выпала на долю трёх великих геометров античной математики – это, конечно же, Евклид, Архимед и Апполоний Пергский. Евклид (написал книгу «Начала», авторитет которой был и остается огромным более 2000 лет), Архимед (развил метод вычисления площадей и объёмов геометрических фигур и тел), Аполлоний Пергский (автор исследования сечений геометрических тел).
А такие два достижения греческой математики далеко пережили своих творцов.
1) греки построили и представили миру математику как целостную науку;
2) греки провозгласили, что законы природы, в том числе законы математики, постижимы для человеческого разума и могут быть использованы в искусстве, а значит, в творении прекрасного.
§3. Страны ислама
Математика Востока, в отличие от греческой, всегда носила более практический характер. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия, механика, оптика. Преследование греческих учёных-нехристиан в Римской империи V—VI веков вызвало их массовое бегство на восток, в Персию и Индию. При дворе Хосрова I они переводили античных классиков на сирийский язык, а два века спустя появились арабские переводы этих трудов. Так было положено начало ближневосточной математической школе. Большое влияние на неё оказала и индийская математика, также испытавшая сильное древнегреческое влияние. В начале IX века научным центром халифата становится Багдад, где халифы создают «Дом мудрости», в который приглашаются виднейшие учёные всего исламского мира —сабии (потомки вавилонских жрецов-звездопоклонников), тюрки и другие. На западе халифата, в испанской Кордове, сформировался другой научный центр, благодаря которому античные знания стали понемногу возвращаться в Европу. Ряд интересных математических задач, стимулировавших развитие сферической геометрии и астрономии, были задачи о расчёте лунного календаря, об определении киблы — точного направления на Мекку.
В целом, эпоха исламской цивилизации в математических науках может быть охарактеризована не как эпоха поиска новых знаний, но — как эпоха передачи и улучшения знаний, полученных от греческих математиков, а, значит, знаний. Включающих в себя законы золотого сечения (диктует идеально красивые пропорции) .
§4. Средневековье, IV - XV века
В это время мы можем отметить расцвет математики как науки.
В конце XII века на базе нескольких монастырских школ был создан Парижский университет. Возникают Оксфорд и Кембридж в Британии.
Первым крупным математиком средневековья стал Леонардо Пизанский, известный под прозвищем Фибоначчи. Множество красивейших замков, башен, фонтанов, храмов построено именно в то время, не без использования математических законов.
§5. Математика у русского народа
Интерес к науке на Руси появился рано. Сохранились сведения о школах при Владимире Святославовиче и Ярославе Мудром (XI век).
Русский народ создал свою собственную систему мер:
1 миля = 7 верстам ( 7,47 км)
7,47 км)
1 верста = 500 саженям ( 1,07 км)
1,07 км)
1 сажень = 3 аршинам = 7 футам ( 2,13 м)
2,13 м)
1 аршин = 16 вершкам = 28 дюймам ( 71,12 см)
71,12 см)
1 фут = 12 дюймам ( 30,48 см)
30,48 см)
1 дюйм = 10 линиям ( 2,54 см)
2,54 см)
1 линия = 10 точкам ( 2,54 мм).
2,54 мм).
Интересно, что на Руси когда говорили о росте человека, то указывали лишь, на сколько вершков он превышает 2 аршина. Поэтому слова «человек 12 вершков роста» означали, что его рост равен 2 аршинам 12 вершкам, то есть 196 см, или о богатырях говорили «Богатырь, косая сажень в плечах», т.е. у такого человека по диагонали от мизинца левой руки до пятки правой ноги почти 2 метра 13 сантиметров. Меткие выражения математического характера, применяемые в речи русичей, делали русский язык звучным и красивым.
§ 6. Искусство счета.
Изучив этот материал, мы поняли, что искусство счета развивалось с развитием человечества. На ранних ступенях развития общества люди почти не умели считать. В те времена, когда человек лишь собирал в лесу плоды и охотился, ему для счета хватало четырех слов: один, два, три и много. Это был еще не счет, а лишь его зародыш. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки.
Впоследствии способность различать друг от друга небольшие совокупности развивалась; появились слова обозначающие числа «четыре», «пять», «шесть», «семь». Последнее слово длительное время обозначало также неопределенно большое количество. Народные пословицы сохранили память о появлении названий числа 7. К примеру, такие как: «семь раз отмерь – один раз отрежь», «у семи нянек дитя без глазу», «семь бед – один ответ», «семеро одного не ждут» и другие.
Однако когда люди начали заниматься животноводством и земледелием, то им уже стало необходимо пересчитывать коз в стаде или количество корзин с выращенными плодами (которых было больше семи), заготовленными на зиму. Поэтому счет получил свое дальнейшее развитие.
Способов счета было придумано немало: делались зарубки на палке по числу предметов, завязывались узлы на веревке, складывались в кучу камешки. Такой вид счета носит название унарной системы счисления, т.е. система счисления, в которой для записи числа применяется только один вид знаков.
Но палку с зарубками с собой не возьмешь, да и камни таскать не очень приятно, а пастуху нужно знать, не отбилась ли какая коза от стада. И тут на помощь приходят пальцы рук — отличный счетный материал, кстати.
Таким образом, можно сделать первый вывод: древний человек хотел учитывать вещи, которыми он владел. Сколько у него инструментов? Сколько оружия? Сколько животных?
Жизнь наших предков была намного проще, но даже они вынуждены были прибегать к использованию числа.
Продолжая изучать литературу по данной теме, мы заметили, что математика - это не только стройная система законов, но и уникальное средство познания красоты. А красота многогранна и многолика.
Рассмотрим применение математики в окружающей нас жизни.
Глава II. Применение законов математики как законов красоты в окружающей нас жизни
§ 1. Математика в мире растений.
Мир растений - величайшее чудо природы, царство красоты и наше целительное богатство. Изучением лекарственных растений занимается наука фитотерапия. Конечно, в этой науке математика играет не последнюю роль. О том, что и здесь применяется математика, мы можем найти сколь угодно много подтверждений. Симметрия листьев, красота цветов, палитра природных окрасов, пропорции стройных деревьев – всё подчинено закону симметричности, пропорциональности и целесообразности.
§ 2. Математика в жизни животных и насекомых.
Мир животных и насекомых - богатый и разнообразный мир живых существ. Этот мир, скажете вы, изучает раздел биологии - зоология. Но позвольте Вам всем возразить! Ведь и здесь не обойтись без математики. Вы когда-нибудь обращали внимание на симметрию крыльев бабочки, на причудливые узоры змеиной кожи, а какие есть красивые по цвету морские и аквариумные рыбки, ведь мы смотрим на них как завороженные. Да таких примеров можно приводить и приводить.



Вот, к примеру, пчёлы - удивительное творение природы. Они маленькие экономисты. Пчелиные соты представляют собой пространственный паркет (шестигранные призмы), поскольку заполняют пространство так, что не остаётся просвета.
Это математический шедевр из воска. А пауки умудряются плести свои паутины, соблюдая строгие пропорции. Как это возможно, ведь пчёлы и пауки не знают высшей математики?




§ 3. Математика геометрических тел и фигур.
Тела и фигуры изучает раздел математики, который называется геометрией. Эта наука возникла в Древней Греции исключительно из практических целей, для измерения участков земли. В том, что с фигурами и телами мы имеем дело в жизни, убеждать, думаем, никого не придётся, а вот понять роль математики в этом можно на примере формул архитектуры, использующей в основе геометрические тела.
§ 4. Математика и культура.
Нам стало интересно, а какое отношение имеет математика к культуре: ведь это и памятники архитектуры, прекрасные скульптуры и, в конце концов, это и живопись. Неужели и здесь мы можем наблюдать «незримое» влияние математики на культуру?! А начать решили с удивительных архитектурных памятников.
Даже сейчас, когда он стоит на развалинах, Парфенон в Афинах - это одно из самых знаменитых сооружений в мире. Он был построен в эпоху расцвета древнегреческой математики.
Фасад Парфенона вписывается в прямоугольник, стороны которого образуют так называемое золотое сечение. Длина прямоугольника больше его ширины примерно в 1,6 раза. А это соотношение в математике принято считать «золотой пропорцией».
Золотое соотношение мы можем увидеть и в пирамиде Хеопса, и в здании собора Парижской Богоматери, и в храме Василия Блаженного на Красной площади.
Золотая пропорция применялась многими античными скульпторами. Известна золотая пропорция статуи Аполлона Бельведерского: рост изображённого человека делится пупочной линией в золотом сечении (талия делит совершенное человеческое тело в отношении золотого сечения примерно )
Скульпторы утверждают, что пропорции мужчин ближе к золотому сечению, нежели пропорции женщин (однако, женщина в обуви на каблуках может оказаться ближе к золотым пропорциям).
Ещё в эпоху Возрождения художники открыли, что любая картина имеет определённые точки, невольно приковывающие внимание, так называемые зрительные центры. Таких точек всего 4, они делят величину изображения по горизонтали и вертикали в золотом сечении. Данное открытие у художников того времени получило название «Золотое сечение» картины.
Переходя к примерам в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.
Портрет Моны Лизы привлекает нас тем, что композиция рисунка построена на «золотых треугольниках».
На этой замечательной картине И. И. Шишкина («Сосновая роща») так же просматриваются мотивы золотого сечения.
Наличие в картине вертикалей и горизонталей, делящих её в отношении золотого сечения, придаёт ей характер уравновешенности и спокойствия.
Золотое сечение можно встретить в бытовых предметах и шрифтах.
§ 5. Математика в живой и неживой природе.
Ещё Гете подчёркивал тенденцию природы к спиральности. Паук плетёт паутину спиралеобразно. Спирально закручивается смерч. Испуганные стада животных разбегается по спирали, а косяки рыб как бы мелькают мимо сети тоже по спирали. Молекула ДНК закручена двойной спиралью. Спираль мы можем увидеть в расположении семян подсолнечника, в шишках сосны, кедра ананасах, кактусах и т.д. Спираль создает не только красоту и порядок, но и модель бытия.
Снежинки: ярче примера очаровательной красоты и порядка в природе вы не найдете. Изучением снежинок занимался знаменитый Рене Декарт. А вообще-то, снежинки - это звёздчатые многоугольники. Они очаровательны ещё и потому, что они симметричны. А симметрия, как сказал Г. Вейль «Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту, совершенство».
Проанализировав приложение математики в окружающей нас жизни, хочется заметить, что красота помогает с радостью воспринимать окружающий мир, а математика даёт возможность открывать всё новые и новые слагаемые красоты. Так и хочется сказать словами поэта
Все в мире связано в единое начало:
В движенье волн – шекспировский сонет,
В симметрии цветка – основы мирозданья,
А в пенье птиц - симфония планет.
У. Блейк
Изучив весь представленный вам материал, мы поняли, что о математике можно говорить вечно. Наверное, поэтому и символ вечности «∞» (бесконечность) мог появиться только с развитием этой науки «Математика». Мы решили перейти к практической части исследования и для начала провели небольшой социологический опрос, который должен нам помочь подтвердить или опровергнуть выдвинутую ранее гипотезу: если математика второстепенная наука, то можно утверждать, что без математических законов красоты можно обойтись; если же нет, то без знания математики вся современная жизнь невозможна.
Практическая часть
Прежде чем сделать окончательный вывод, что для нас математика, мы предлагаем изучить результаты социологического опроса.
Цель опроса - изучение общественного мнения по данной теме.
Опрос вёлся по следующим направлениям:
1) математика - это красота,
2) нужны ли математические законы красоты в жизни людей,
3) где находят свое применение математические законы красоты.
Опрос проводился среди следующих категорий:
1) учащиеся 7. 8, 9, 11 классов МБОУ Шиковской СШ,
2) учителя МБОУ Шиковской СШ (выборочно),
3) родители учащихся 7. 8, 9, 11 классов МБОУ Шиковской СШ (выборочно)
В опросе приняли участие 27 человек.
Вот что у нас получилось:
I направление. Математика - это красота
Результаты данного направления говорят о том, что математика является красотой для 17 человек из числа всех опрошенных, для 8 человек математика - это просто наука, 2 человека затруднялись ответить, что для них математика.
II направление. Нужны ли математические законы красоты в жизни людей?
Нужны ли математические законы красоты в жизни людей?
Данная диаграмма показывает, что математические законы красоты нужны 74% (20 человек из 27) и не нужны 26% (7 человек из 27).
III направление. Где находят свое применение математические законы красоты?
Ответы на этот вопрос приведены в следующей таблице.
| 5 | |
| 2 | |
| 2 | |
| 7 | |
| 1 | |
| 2 | |
| 8 |
всего: 27 человек
Так отвечали не только дети, но и взрослые.
Заключение
Результаты исследования
Итак, гипотеза, которую мы выдвинули в начале нашего исследования, на практике не подтвердилась. Следовательно, предположение о том, что математические законы красоты не важны - неверно.
Таким образом, на основании изученной литературы и анализа результатов общественного мнения, мы можем сделать вывод о том, что без знания математических законов красоты вся современная жизнь невозможна. Например, у нас не было бы хороших домов с красивыми изящными линиями, т. к. строители должны уметь измерять, считать, сооружать. Наша одежда была бы грубой, т. к. её нужно хорошо, красиво скроить. Не было бы ни прекрасно спланированных парковых зон, никакой лёгкой промышленности и тысячи других вещей, составляющих часть нашей цивилизации.
В данной работе мы выяснили, математика - часть мира, напрямую связанная с категорией красоты, которая создаётся по математическим формулам; часть мира, в котором мы живём.
Поэтому мы может с полной и абсолютной уверенностью воскликнуть:
Математика - это красота.!
Список использованных источников информации
1. За страницами учебника математики. - И. Я. Депман, Н. Я. Виленкин
2. С математикой в путь. - Н. Лэнгдон, Ч. Снейп
3. www.abc-people.com/data/leonardov/zolot_sech-txt.htm - Золотое сечение.
4. http://tmn.fio.ru/works/04x/304/p4_21k.htm - Биология.
5. http://festival.1september.ru/2004_2005/index.php?numb_artic=213063-
История математики.
6. http://bse.sci-lib.com/article048077.html - Золотое сечение.
7. http://www.mjagkov.de/ser/archives/42-,.html
8. http://namangan34.connect.uz/lifemath/links.php - Живая математика
9. Учебник «Математика – 6». – Алдамуратова Т.А., Байшоланов Т.С.,
издательство «Атамұра», 2011 год.
multiurok.ru











